java常用的8种排序方法
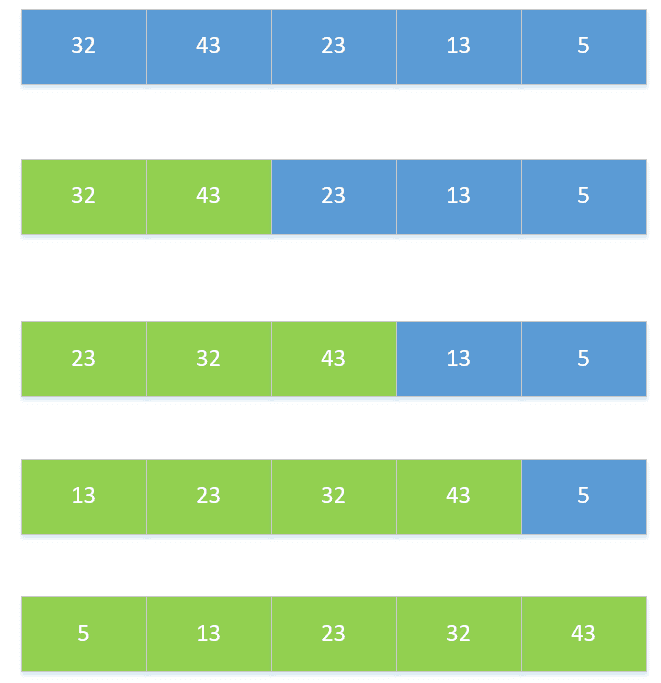
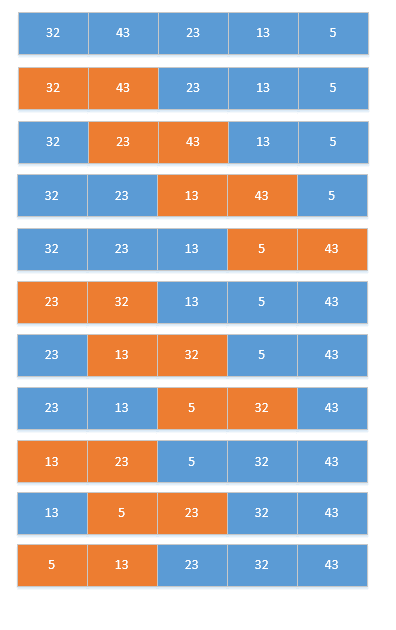
1.直接插入排序
经常碰到这样一类排序问题:把新的数据插入到已经排好的数据列中。
- 将第一个数和第二个数排序,然后构成一个有序序列
- 将第三个数插入进去,构成一个新的有序序列。
-
对第四个数、第五个数……直到最后一个数,重复第二步。
如何写写成代码:
- 首先设定插入次数,即循环次数,for(int i=1;i
- 设定插入数和得到已经排好序列的最后一个数的位数。insertNum和j=i-1。
- 从最后一个数开始向前循环,如果插入数小于当前数,就将当前数向后移动一位。
- 将当前数放置到空着的位置,即j+1。
代码实现如下:
public class Main {
public static void insertSort(int[] a){
int temp = 0 ,j;
for (int i = 1; i < a.length; i++){
if (a[i - 1] > a[i]){
temp = a[i];
j = i;
while (j > 0 && a[j - 1] > temp){
a[j] = a[j - 1];
j--;
}
a[j] = temp;
}
}
}
public static void main(String[] args) {
int[] x = { 6, 2, 4, 1, 5, 9 };
insertSort(x);
for (int i : x) {
System.out.print(i+",");
}
}
}2.希尔排序
对于直接插入排序问题,数据量巨大时。
- 将数的个数设为n,取奇数k=n/2,将下标差值为k的书分为一组,构成有序序列。
- 再取k=k/2 ,将下标差值为k的书分为一组,构成有序序列。
-
重复第二步,直到k=1执行简单插入排序。
如何写成代码:
- 首先确定分的组数。
- 然后对组中元素进行插入排序。
- 然后将length/2,重复1,2步,直到length=0为止。
代码实现如下:
public void sheelSort(int[] a){
int d = a.length;
d=d/2;
while (d!=0) {
for (int i = x + d; i < a.length; i += d) {//组中的元素,从第二个数开始
for (int x = 0; x < d; x++) {//分的组数
int temp = a[i];//要插入的元素
int j = i - d;//j为有序序列最后一位的位数
a[j + d] = a[j];//向后移动d位
for (; j >= 0 && temp < a[j]; j -= d) {//从后往前遍历。
}
}
a[j + d] = temp;
}
}
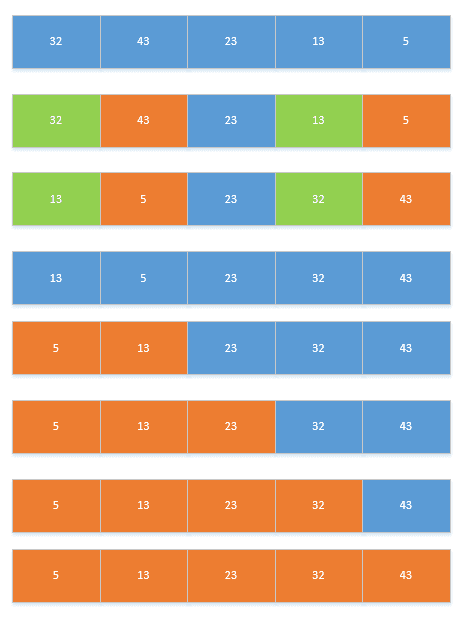
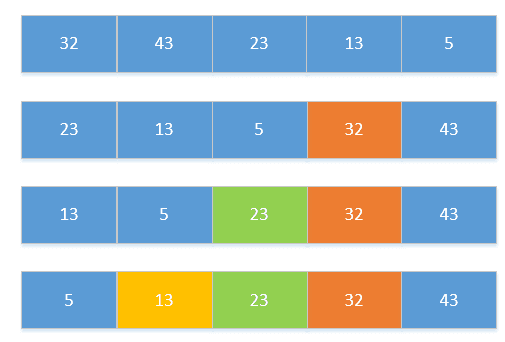
}3.简单选择排序
常用于取序列中最大最小的几个数时。
(如果每次比较都交换,那么就是交换排序;如果每次比较完一个循环再交换,就是简单选择排序。)
- 遍历整个序列,将最小的数放在最前面。
- 遍历剩下的序列,将最小的数放在最前面。
-
重复第二步,直到只剩下一个数。
如何写成代码:
- 首先确定循环次数,并且记住当前数字和当前位置。
- 将当前位置后面所有的数与当前数字进行对比,小数赋值给key,并记住小数的位置。
- 比对完成后,将最小的值与第一个数的值交换。
- 重复2、3步。
代码实现如下:
public void selectSort(int[] a) {
int length = a.length;
for (int i = 0; i < length; i++) {//循环次数
int key = a[i];
int position=i;
if (a[j] < key) {
for (int j = i + 1; j < length; j++) {//选出最小的值和位置
key = a[j];
a[i]=key;
position = j;
}
}
a[position]=a[i];//交换位置
}
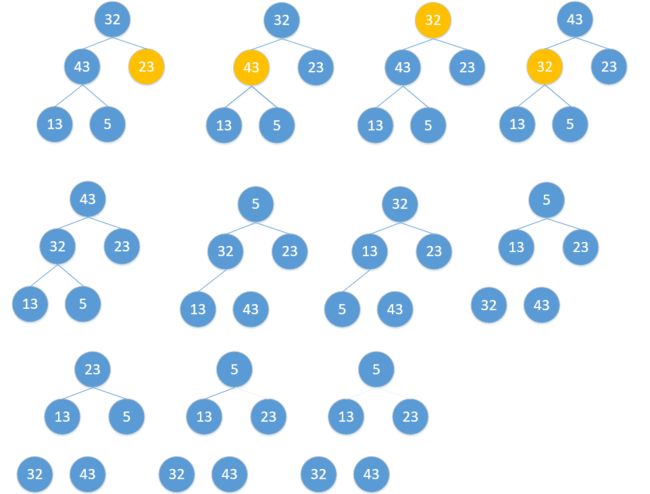
}4.堆排序
对简单选择排序的优化。
- 将序列构建成大顶堆。
- 将根节点与最后一个节点交换,然后断开最后一个节点。
-
重复第一、二步,直到所有节点断开。
代码实现如下:
public void heapSort(int[] a){
System.out.println("开始排序");
int arrayLength=a.length;
for(int i=0;i=0;i--){
//k保存正在判断的节点
//如果当前k节点的子节点存在
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
if(biggerIndex 5.冒泡排序
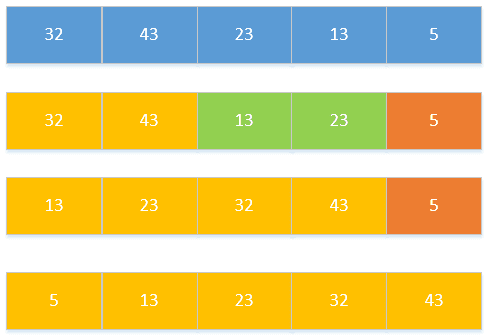
一般不用。
- 将序列中所有元素两两比较,将最大的放在最后面。
- 将剩余序列中所有元素两两比较,将最大的放在最后面。
-
重复第二步,直到只剩下一个数。
如何写成代码:
- 设置循环次数。
- 设置开始比较的位数,和结束的位数。
- 两两比较,将最小的放到前面去。
- 重复2、3步,直到循环次数完毕。
代码实现如下:
public void bubbleSort(int[] a){
int length=a.length;
for(int i=0;ia[j+1]){
for(int j=0;j 6.快速排序
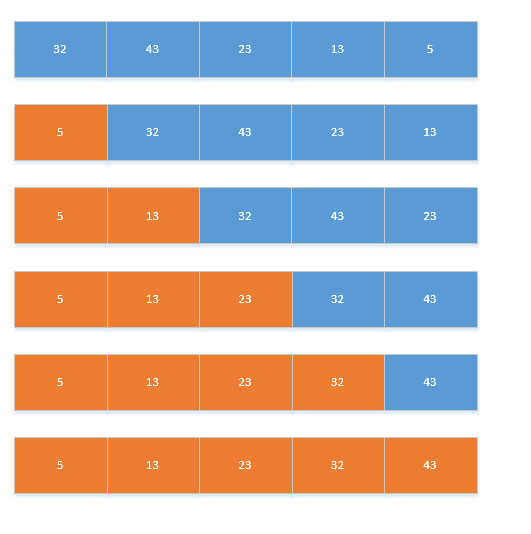
要求时间最快时。
- 选择第一个数为p,小于p的数放在左边,大于p的数放在右边。
-
递归的将p左边和右边的数都按照第一步进行,直到不能递归。
代码实现如下:
public static void quickSort(int[] numbers, int start, int end) {
if (start < end) {
int temp; // 记录临时中间值
int base = numbers[start]; // 选定的基准值(第一个数值作为基准值)
while ((numbers[i] < base) && (i < end))
int i = start, j = end;
do {
i++;
if (i <= j) {
while ((numbers[j] > base) && (j > start))
j--;
temp = numbers[i];
}
numbers[i] = numbers[j];
numbers[j] = temp;
i++;
j--;
} while (i <= j);
}
if (start < j)
quickSort(numbers, start, j);
if (end > i)
quickSort(numbers, i, end);
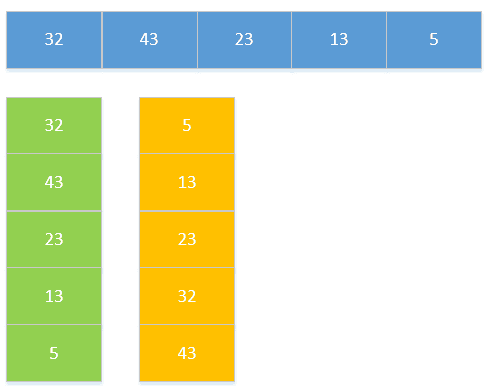
} 7.归并排序
速度仅次于快排,内存少的时候使用,可以进行并行计算的时候使用。
- 选择相邻两个数组成一个有序序列。
- 选择相邻的两个有序序列组成一个有序序列。
-
重复第二步,直到全部组成一个有序序列。
代码实现如下:
public class MergeSortTest {
public static void main(String[] args) {
int[] data = new int[] { 5, 3, 6, 2, 1, 9, 4, 8, 7 };
print(data);
mergeSort(data);
System.out.println("排序后的数组:");
print(data);
}
public static void mergeSort(int[] data) {
sort(data, 0, data.length - 1);
}
public static void sort(int[] data, int left, int right) {
if (left >= right)
return;
// 找出中间索引
int center = (left + right) / 2;
// 对左边数组进行递归
sort(data, left, center);
// 对右边数组进行递归
sort(data, center + 1, right);
// 合并
merge(data, left, center, right);
print(data);
}
/**
* 将两个数组进行归并,归并前面2个数组已有序,归并后依然有序
*
* @param data
* 数组对象
* @param left
* 左数组的第一个元素的索引
* @param center
* 左数组的最后一个元素的索引,center+1是右数组第一个元素的索引
* @param right
* 右数组最后一个元素的索引
*/
public static void merge(int[] data, int left, int center, int right) {
// 临时数组
int[] tmpArr = new int[data.length];
// 右数组第一个元素索引
int mid = center + 1;
// third 记录临时数组的索引
int third = left;
// 缓存左数组第一个元素的索引
int tmp = left;
while (left <= center && mid <= right) {
// 从两个数组中取出最小的放入临时数组
if (data[left] <= data[mid]) {
tmpArr[third++] = data[left++];
} else {
tmpArr[third++] = data[mid++];
}
}
// 剩余部分依次放入临时数组(实际上两个while只会执行其中一个)
while (mid <= right) {
tmpArr[third++] = data[mid++];
}
while (left <= center) {
tmpArr[third++] = data[left++];
}
// 将临时数组中的内容拷贝回原数组中
// (原left-right范围的内容被复制回原数组)
while (tmp <= right) {
data[tmp] = tmpArr[tmp++];
}
}
public static void print(int[] data) {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i] + "\t");
}
System.out.println();
}
} 8.基数排序
用于大量数,很长的数进行排序时。
- 将所有的数的个位数取出,按照个位数进行排序,构成一个序列。
-
将新构成的所有的数的十位数取出,按照十位数进行排序,构成一个序列。
代码实现如下:
public void sort(int[] array) {
//首先确定排序的趟数;
for (int i = 1; i < array.length; i++) {
int max = array[0];
max = array[i];
if (array[i] > max) {
}
}
while (max > 0) {
int time = 0;
//判断位数;
max /= 10;
List queue = new ArrayList();
time++;
}
//建立10个队列;
ArrayList queue1 = new ArrayList();
for (int i = 0; i < 10; i++) {
queue.add(queue1);
}
//分配数组元素;
//进行time次分配和收集;
for (int i = 0; i < time; i++) {
int x = array[j] % (int) Math.pow(10, i + 1) / (int) Math.pow(10, i);
for (int j = 0; j < array.length; j++) {
//得到数字的第time+1位数;
queue.set(x, queue2);
ArrayList queue2 = queue.get(x);
queue2.add(array[j]);
}
while (queue.get(k).size() > 0) {
int count = 0;//元素计数器;
//收集队列元素;
for (int k = 0; k < 10; k++) {
count++;
ArrayList queue3 = queue.get(k);
array[count] = queue3.get(0);
queue3.remove(0);
}
}
}
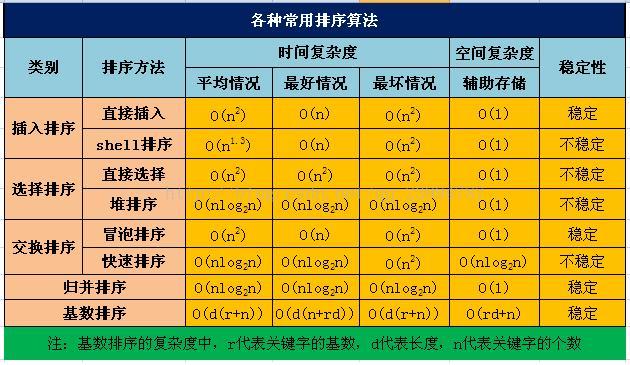
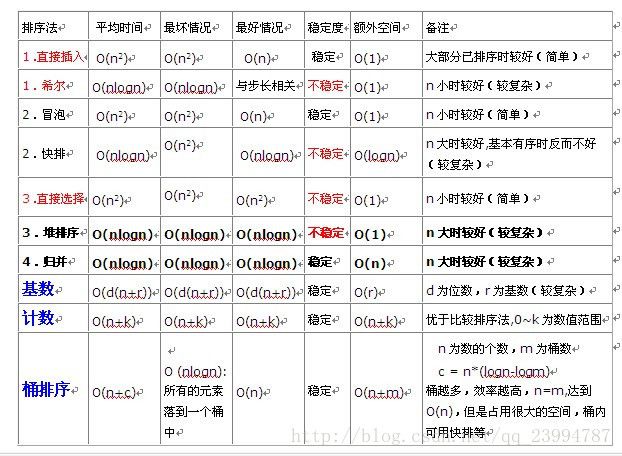
} 1.O(n^2)性能分析
平均性能为O(n^2)的有:直接插入排序,选择排序,冒泡排序
1.在数据规模较小时(9W内),直接插入排序,选择排序差不多。当数据较大时,冒泡排序算法的时间代价最高。
2.性能为O(n^2)的算法基本上是相邻元素进行比较,基本上都是稳定的。
2.O(nlogn)性能分析
平均性能为O(nlogn)的有:快速排序,归并排序,希尔排序,堆排序。其中,快排是最好的, 其次是归并和希尔,堆排序在数据量很大时效果明显。
这四种排序可看作为“先进算法”,其中,快排效率最高,但在待排序列基本有序的情况下,会变成冒泡排序,接近O(n^2).
希尔排序对增量的标准没有较为满意的答案,增量对性能会有影响。
归并排序效率非常不错,在数据规模较大的情况下,比希尔排序和堆排序要好。
多数先进的算法都是因为跳跃式的比较,降低了比较次数,但牺牲了排序的稳定性。
3. 插入排序,冒泡排序,二叉树排序,归并排序都是稳定的,选择排序,希尔排序,快速排序,堆排序是不稳定的。
如何选择排序算法?
1.数据规模较小
(1)待排序列基本序的情况下,可以选择直接插入排序;
(2)对稳定性不作要求宜用选择排序,对稳定性有要求宜用插入或冒泡
2.数据规模不是很大
(1)完全可以用内存空间,序列杂乱无序,对稳定性没有要求,快速排序,此时要付出log(N)的额外空间。
(2)序列本身可能有序,对稳定性有要求,空间允许下,宜用归并排序
3.海量级别的数据,必须按块放在外存上
(1)对稳定性有求,则可考虑归并排序。
(2)对稳定性没要求,宜用堆排序
4.序列初始基本有序(正序),宜用直接插入,冒泡,随机快排
各排序算法整体分析
冒泡排序、插入排序、希尔排序以及快速排序对数据的有序性比较敏感,尤其是冒泡排序和插入排序;
选择排序不关心表的初始次序,它的最坏情况的排序时间与其最佳情况没多少区别,其比较次数为 n(n-1)/2,但选择排序可以 非常有效的移动元素。因此对次序近乎正确的表,选择排序可能比插入排序慢很多。
冒泡排序在最优情况下只需要经过n-1次比较即可得出结果(即对于完全正序的表),最坏情况下也要进行n(n-1)/2 次比较,与选择排序的比较次数相同,但数据交换的次数要多余选择排序,因为选择排序的数据交换次数顶多为 n-1,而冒泡排序最坏情况下的数据交换n(n-1)/2 。冒泡排序不一定要进行 趟,但由于它的记录移动次数较多,所以它的平均时间性能比插入排序要差一些。
插入排序在最好的情况下有最少的比较次数 ,但是它在元素移动方面效率非常低下,因为它只与毗邻的元素进行比较,效率比较低。
希尔排序实际上是预处理阶段优化后的插入排序,一般而言,在 比较大时,希尔排序要明显优于插入排序。
快速排序采用的“大事化小,小事化了”的思想,用递归的方法,将原问题分解成若干规模较小但与原问题相似的子问题进行求解。快速算法的平均时间复杂度为O(nlogn) ,平均而言,快速排序是基于关键字比较的内部排序算法中速度最快者;但是由于快速排序采用的是递归的方法,因此当序列的长度比较大时,对系统栈占用会比较多。快速算法尤其适用于随机序列的排序。
因此,平均而言,对于一般的随机序列顺序表而言,上述几种排序算法性能从低到高的顺序大致为:冒泡排序、插入排序、选择排序、希尔排序、快速排序。但这个优劣顺序不是绝对的,在不同的情况下,甚至可能出现完全的性能逆转。
对于序列初始状态基本有正序,可选择对有序性较敏感的如插入排序、冒泡排序、选择排序等方法
对于序列长度 比较大的随机序列,应选择平均时间复杂度较小的快速排序方法。
各种排序算法都有各自的优缺点,适应于不同的应用环境,因此在选择一种排序算法解决实际问题之前,应当先分析实际问题的类型,再结合各算法的特点,选择一种合适的算法。