linux 系统物理页面的管理----如何记录哪个页框是空闲的
linux 系统中,用 binary buddy allocator (二进制伙伴分配算法)去管理物理页面。
1、 Managing Free Blocks
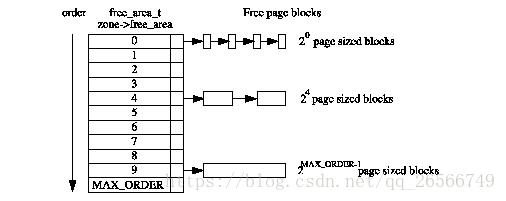
linux 系统中将所有的空闲页面分为11个空闲链表,分别管理着1,2,4,8,。。。1024个连续的空闲页框。如2^0=1,这个链表中装的是1个页框大小的内存,2^10 表示装着1024个连续页框的大小的内存。这些链表称为 freelist.每个块的第一个页框的物理地址是该块大小的整数倍。例如,大小为16个页框的块,其起始地址是16*2^12的倍数.
满足以下条件的两个块称为伙伴:
1)两个块大小相同;
2)两个块地址连续;
3)两个块必须是同一个大块中分离出来的
2)两个块地址连续;
3)两个块必须是同一个大块中分离出来的

Linux2.6为每个管理区使用不同的伙伴系统,内核空间分为三种区,DMA,NORMAL,HIGHMEM,对于每一种区,都有对于的伙伴算法.
每个区域都有一个名为free_area [MAX_ORDER]的free_area_t结构数组
typedef struct free_area_struct {
struct list_head free_list; //free_list A linked list of free page blocks;
unsigned long *map; //map A bitmap representing the state of a pair of buddies.使用1 bit来表示伙伴的状态,如果该对伙伴的页面都是空闲的或者两者都是满的则该位为零,如果仅使用一个伙伴则该位为1。
} free_area_t; #define MARK_USED(index,order,area) __change_bit((index) >> (1+(order)),(area)->map) //index是全局mem_map数组中页面的索引。 通过将其向右移动1+oder,代表该对伙伴的在map 中的w位。
Buddy算法的分配原理:
假如系统需要4(2*2)个页面大小的内存块,该算法就到free_area[2]中查找,如果链表中有空闲块,就直接从中摘下并分配出去。如果没有,算法将顺着数组向上查找free_area[3],如果free_area[3]中有空闲块,则将其从链表中摘下,分成等大小的两部分,前四个页面作为一个块插入free_area[2],后4个页面分配出去,free_area[3]中也没有,就再向上查找,如果free_area[4]中有,就将这16(2*2*2*2)个页面等分成两份,前一半挂如free_area[3]的链表头部,后一半的8个页等分成两等分,前一半挂free_area[2]
的链表中,后一半分配出去。假如free_area[4]也没有,则重复上面的过程,知道到达free_area数组的最后,如果还没有则放弃分配。
的链表中,后一半分配出去。假如free_area[4]也没有,则重复上面的过程,知道到达free_area数组的最后,如果还没有则放弃分配。
Buddy算法的释放原理:
内存的释放是分配的逆过程,也可以看作是伙伴的合并过程。当释放一个块时,先在其对应的链表中考查是否有伙伴存在,如果没有伙伴块,就直接把要释放的块挂入链表头;如果有,则从链表中摘下伙伴,合并成一个大块,然后继续考察合并后的块在更大一级链表中是否有伙伴存在,直到不能合并或者已经合并到了最大的块(2*2*2*2*2*2*2*2*2个页面)。整个过程中,位图扮演了重要的角色,位图的某一位对应两个互为伙伴的块,为1表示其中一块已经分配出去了,为0表示两块都空闲。伙伴中无论是分配还是释放都只是相对的位图进行异或操作。分配内存时对位图的操作是为释放过程服务,释放过程根据位图判断伙伴是否存在,如果对相应位的异或操作得1,则没有伙伴可以合并,如果异或操作得0,就进行合并,并且继续按这种方式合并伙伴,直到不能合并为止。
伙伴算法的优缺点
优点:
较好的解决外部碎片问题
当需要分配若干个内存页面时,用于DMA的内存页面必须连续,伙伴算法很好的满足了这个要求
只要请求的块不超过512个页面(2K),内核就尽量分配连续的页面。
针对大内存分配设计。
缺点:
1. 合并的要求太过严格,只能是满足伙伴关系的块才能合并,比如第1块和第2块就不能合并。
2. 碎片问题:一个连续的内存中仅仅一个页面被占用,导致整块内存区都不具备合并的条件
3. 浪费问题:伙伴算法只能分配2的幂次方内存区,当需要8K(2页)时,好说,当需要9K时,那就需要分配16K(4页)的内存空间,但是实际只用到9K空间,多余的7K空间就被浪费掉。
4. 算法的效率问题: 伙伴算法涉及了比较多的计算还有链表和位图的操作,开销还是比较大的,如果每次2^n大小的伙伴块就会合并到2^(n+1)的链表队列中,那么2^n大小链表中的块就会因为合并操作而减少,但系统随后立即有可能又有对该大小块的需求,为此必须再从2^(n+1)大小的链表中拆分,这样的合并又立即拆分的过程是无效率的。