数据结构与算法---二叉堆和二叉堆排序(python实现)

一、什么是二叉堆

1. 堆的定义：

堆（heap），这里指的堆是一种数据结构，不是内存模型中的堆。堆通常可以看作为一棵树，但这棵树得满足以下条件：

a.  堆中任意节点的值总是不大于（不小于）其子节点的值；

b.  堆总是一颗完全树。

将任意节点不大于其子节点的堆叫做最小堆或小根堆，而将任意节点不小于其子节点的堆叫做最大堆或者大根堆。常见的堆有二叉堆，左倾堆，斜堆，二项堆，斐波那契堆等等。

2. 二叉堆：

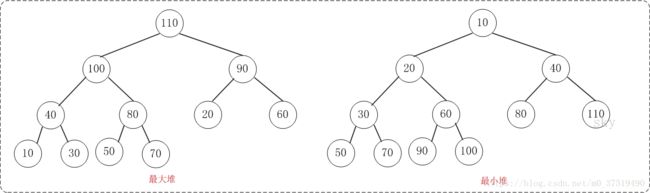
二叉堆是完全二叉树，它分为两种：最大堆和最小堆。

最大堆：父结点的键值总是大于或等于任何一个子节点的键值；最小堆：父结点的键值总是小于或等于任何一个子节点的键值。示意图如下：

二、二叉堆的存储

二叉堆是一颗二叉树，因此我们很容易想到使用链式存储，但是二叉堆是一颗完全二叉树，因此我们可以使用数组这种更简单高效的存储方式。

我们将二叉堆的第一个元素放在数组索引的0的位置，也可以放在索引为1的位置。当然，它们的本质是一样的。

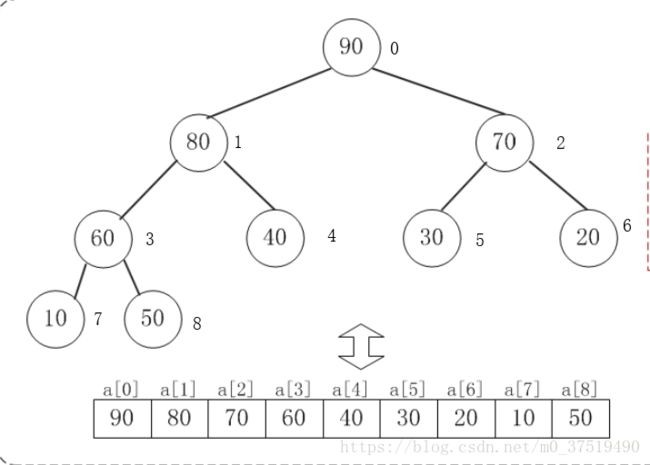
当第一个元素放在索引为0的位置上时：

1. 索引为 i 的左孩子的索引为（2*i + 1）

2. 索引为 i 的右孩子的索引为 （2*i + 2）

3. 索引为 i 的父节点的索引为 （i - 1）/ 2（计算机里取整）

二叉堆及其数组存储方式如下：

当第一个元素放在索引为1的位置上时：

1. 索引为 i 的左孩子的索引为（2*i ）

2. 索引为 i 的右孩子的索引为 （2*i + 1）

3. 索引为 i 的父节点的索引为 （i ）/ 2（计算机里取整）

二叉堆及其数组存储方式如下：

三、二叉堆的基本操作：shift_up与shift_down

我们以最大堆来演示二叉堆的插入与删除对应的shift_up与shift_down操作

1. 插入数据---shift_up:

例如，在最大堆[90,80,70,60,40,30,20,10,50]中添加85，需要执行的步骤如下：

插入数据基本过程如下：

a.  将数据加入到最大堆的末尾，即数组最后

b. 然后通过shift_up操作把数据尽可能的往上挪，直到挪不动为止

因此，插入的最关键步骤为shift_up,最大堆插入的代码如下：

class MaxHeap:
    heap = []

    @staticmethod
    def insert(num):
        MaxHeap.heap.append(num)
        MaxHeap.shift_up()

    @staticmethod
    def shift_up():
        current_id = len(MaxHeap.heap) - 1
        parent_id = (current_id - 1)//2
        while current_id > 0:
            if MaxHeap.heap[parent_id] >= MaxHeap.heap[current_id]:
                break
            else:
                MaxHeap.heap[parent_id], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[parent_id]
                current_id = parent_id
                parent_id = (current_id -1)//2

2. 删除数据---shift_down:

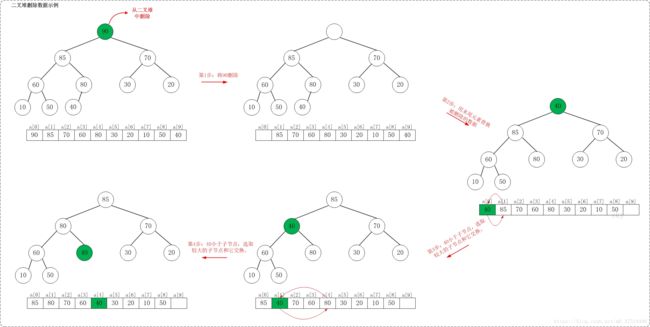
如例，从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90，需要执行的步骤如下：

删除数据的步骤如下：

a. 删除该数据m，但数组结构不变，即其他数据位置不发生移动

b. 将数组最后一个数据n移动到刚才删除的数据m的索引处

c. 通过shift_down操作，把数据n，尽量往下挪，直到生于的数组重新成为最大堆

因此，删除的最关键步骤为shift_down,最大堆删除的代码如下：

class MaxHeap:
    heap = [90,85,70,60,80,30,20,10,50,40]

    @staticmethod
    def insert(num):
        MaxHeap.heap.append(num)
        MaxHeap.shift_up()

    @staticmethod
    def shift_up():
        current_id = len(MaxHeap.heap) - 1
        parent_id = (current_id - 1)//2
        while current_id > 0:
            if MaxHeap.heap[parent_id] >= MaxHeap.heap[current_id]:
                break
            else:
                MaxHeap.heap[parent_id], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[parent_id]
                current_id = parent_id
                parent_id = (current_id -1)//2

    @staticmethod
    def delate(num):
        temp = MaxHeap.heap.pop()
        ind = MaxHeap.heap.index(num)
        MaxHeap.heap[ind] = temp
        MaxHeap.shift_down(ind)

    @staticmethod
    def shift_down(ind):
        current_id = ind
        child_id_left = current_id * 2 + 1
        child_id_right = current_id * 2 + 2
        while current_id < len(MaxHeap.heap) - 1:
            #如果当前节点为叶子节点，shift_down完成
            if current_id * 2 + 1 > len(MaxHeap.heap) - 1:
                break
            #如果当前节点只有左孩子没有右孩子
            if current_id * 2 + 1 == len(MaxHeap.heap) - 1:
                if MaxHeap.heap[current_id] > MaxHeap.heap[-1]:
                    break
                else:
                    MaxHeap.heap[current_id], MaxHeap.heap[-1] = MaxHeap.heap[-1], MaxHeap.heap[current_id]
                    break
            #如果当前节点既有左孩子又有右孩子
            if MaxHeap.heap[current_id] > max(MaxHeap.heap[child_id_left], MaxHeap.heap[child_id_right]):
                break
            else:
                if MaxHeap.heap[child_id_right] > MaxHeap.heap[child_id_left]:
                    MaxHeap.heap[child_id_right], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[child_id_right]
                    current_id = child_id_right
                    child_id_left = current_id * 2 + 1
                    child_id_right = current_id * 2 + 2
                else:
                    MaxHeap.heap[child_id_left], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[child_id_left]
                    current_id = child_id_left
                    child_id_left = current_id * 2 + 1
                    child_id_right = current_id * 2 + 2

四、基础堆排序和Heapify

1. 基础排序

有了堆的基本操作，实现堆的排序就比较简单了，用最大堆实现升序排序步骤如下：

a. 将待排序列表依次插入

b. 依次取出堆顶元素并放进原列表对应位置

代码实现如下：

class MaxHeap:
    heap = []

    @staticmethod
    def insert(num):
        MaxHeap.heap.append(num)
        MaxHeap.shift_up()

    @staticmethod
    def shift_up():
        current_id = len(MaxHeap.heap) - 1
        parent_id = (current_id - 1)//2
        while current_id > 0:
            if MaxHeap.heap[parent_id] >= MaxHeap.heap[current_id]:
                break
            else:
                MaxHeap.heap[parent_id], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[parent_id]
                current_id = parent_id
                parent_id = (current_id -1)//2

    @staticmethod
    def delate(num):
        temp = MaxHeap.heap.pop()

        ind = MaxHeap.heap.index(num)
        MaxHeap.heap[ind] = temp
        MaxHeap.shift_down(ind)



    @staticmethod
    def shift_down(ind):
        current_id = ind
        child_id_left = current_id * 2 + 1
        child_id_right = current_id * 2 + 2
        while current_id < len(MaxHeap.heap) - 1:
            #如果当前节点为叶子节点，shift_down完成
            if current_id * 2 + 1 > len(MaxHeap.heap) - 1:
                break
            #如果当前节点只有左孩子没有右孩子
            if current_id * 2 + 1 == len(MaxHeap.heap) - 1:
                if MaxHeap.heap[current_id] > MaxHeap.heap[-1]:
                    break
                else:
                    MaxHeap.heap[current_id], MaxHeap.heap[-1] = MaxHeap.heap[-1], MaxHeap.heap[current_id]
                    break
            #如果当前节点既有左孩子又有右孩子
            if MaxHeap.heap[current_id] > max(MaxHeap.heap[child_id_left], MaxHeap.heap[child_id_right]):
                break
            else:
                if MaxHeap.heap[child_id_right] > MaxHeap.heap[child_id_left]:
                    MaxHeap.heap[child_id_right], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[child_id_right]
                    current_id = child_id_right
                    child_id_left = current_id * 2 + 1
                    child_id_right = current_id * 2 + 2
                else:
                    MaxHeap.heap[child_id_left], MaxHeap.heap[current_id] = MaxHeap.heap[current_id], MaxHeap.heap[child_id_left]
                    current_id = child_id_left
                    child_id_left = current_id * 2 + 1
                    child_id_right = current_id * 2 + 2

    @staticmethod
    def extract_max():
        num = MaxHeap.heap[0]
        try:
            MaxHeap.delate(num)
            return num
        except:
            return num

    @staticmethod
    def heap_sort(arr):
        for n in arr:
            MaxHeap.insert(n)
        for i in range(len(arr)):
            arr[i] = MaxHeap.extract_max()

2. Heapify

基础堆排序中，将n个元素逐个插入到一个空堆中，算法复杂度是O(nlogn)

而下面介绍的Heapify，对n个元素的建堆，算法复杂度是O(n)

Heapify算法过程如下：

----堆的第一个元素从索引0开始，堆元素个数为n

a. 找到待建堆的二叉树最后一个非叶子节点，索引为 m =(n - 1)/2

b. 从索引m到0，依次执行shift_down 操作

二叉树的倒数第一层满足二叉堆性质，因此，从倒数第二层开始，通过shift_down 逐层的将其转换为二叉堆。

代码如下（附带通过heapify的排序算法）：

    @staticmethod
    def heapify(arr):
        MaxHeap.heap = arr
        n = (len(arr) - 1)//2
        while n >= 0:
            MaxHeap.shift_down(n)
            n -= 1

    @staticmethod
    def heap_sort2(arr):
        MaxHeap.heapify(arr)
        res = []
        for i in range(len(arr)):
            res.append(MaxHeap.extract_max())
        return res

五、原地堆排序

在上一节中，无论是堆的基础排序还是基于heapify的排序，都需要额外的开辟一片空间存放排序。空间复杂度为O(n),

接下来要讲的原地堆排序的空间复杂度为O(1), 算法过程分析如下：

a. 由heapify对n个元素的列表建堆

b. 将堆顶元素与堆尾元素互换，堆大小减一

c. 对堆顶元素执行shift_down操作

d. 依次循环b,c。当堆中元素个数为0时为止

代码如下：

    @staticmethod
    def heap_sort3(arr):
        MaxHeap.heapify(arr)
        for i in range(len(arr)-1, -1, -1):
            MaxHeap.heap[i], MaxHeap.heap[0] = MaxHeap.heap[0], MaxHeap.heap[i]  #将堆顶元素与堆尾元素互换
            MaxHeap.shift_down(0, i)

六、堆的优势

若使用堆做静态数组的排序，它的时间复杂度与快速排序相比并没有优势，实际上一般情况下要慢于快速排序。

那堆排序的优势在哪呢？

堆，在解决动态排序问题时，有较大优势。

问题1. 动态选择优先级最高的任务执行

很多情况下，我们需要使用优先队列来解决实际问题，如操作系统选择优先级最高的进程使用CPU，而进程随时都会有新进程产生，也会有老进程死亡，而且各进程的优先级也会动态变化。这种时候，如果每次都用排序算法对所有进程优先级进行排序，可以想象耗时是巨大的。而此时堆来解决优先队列就显示出巨大优势，插入新元素，重建最大堆，删除元素，这些操作的时间复杂度均为O(logn)。

问题2. 从N个元素中选出前M个（N巨大而M相对很小，如N=10000000，M=10）

用快速排序算法时间复杂度为NlogN, 而用堆排序时间复杂度为NlogM

当然对于问题2，对快排进行改进，也可提高效率，具体实现方法还没想太清楚。

综上：堆的最大优势就在使用堆实现优先队列。

参考博客：

https://www.cnblogs.com/skywang12345/p/3610187.html

https://coding.imooc.com/class/207.html