CRC32的FPGA并行实现原理及MATLAB仿真
其实crc已经反反复复看了好多遍了,每次总是看到一半就放弃了,觉得太简单,都有现成的东西,没必要搞懂,纯属浪费时间,但是又总是如鲠在喉,一如既往的纠结……这两天终于明白了它并行实现的原理,写个总结。
1 串行实现(单bit实现)
crc的实现原理很简单,做二进制除法得到余数就可以了,贴一个对我理解CRC很有帮助的一篇文章
我学习CRC32、CRC16、CRC原理和算法的总结(与WINRAR结果一致)
这里面的叫法是直接计算法和驱动表法,可能是因为软件实现和硬件实现不一样的原因吧,我这里叫串行实现和并行实现。
2 并行实现(8bit并行)
串行实现的效率是非常低的,特别是数据量很大的时候。
2.1 并行实现的思想
并行实现的原理主要利用的是异或(XOR)的交换律
A ⊕ B 1 ⊕ B 2 ⊕ B 3 = A ⊕ ( B 1 ⊕ B 2 ⊕ B 3 ) A⊕B_1⊕B_2⊕B_3 = A⊕(B_1⊕B_2⊕B_3) A⊕B1⊕B2⊕B3=A⊕(B1⊕B2⊕B3)
我们知道二进制除法其实就是不停的移位与被除数进行异或,像下面这样

可以看到经过3次移位异或得到了余数0010,我们把前面的零补上来看更直观

现在把交换律用上

(上面的图应该编号 B 1 、 B 2 、 B 3 B_1、B_2、B_3 B1、B2、B3的,不过算了)
所以一旦我们知道了进来的4个bit是1010,我们就知道接下来的除法是怎么移位的,4bit有16种可能,8bit则有256种可能,这样我们就可以通过查表的方式直接实现4bit 的二进制除法(将所有可能的 ( B 1 ⊕ B 2 ⊕ … … ) (B_1⊕B_2⊕……) (B1⊕B2⊕……)存起来)。但是FPGA实现则不是查表来实现的,因为8bit实现CRC32的话就需要32*256bit的存储,太浪费资源了,FPGA是直接算出 ( B 1 ⊕ B 2 ⊕ … … ) ⊕ A (B_1⊕B_2⊕……)⊕A (B1⊕B2⊕……)⊕A的结果。
2.2 公式推导
那 ( B ⊕ B ⊕ … … ) (B⊕B⊕……) (B⊕B⊕……)怎么算呢?我们通过公式来理解会比较好,这里有一篇论文
CRC查询表及其并行矩阵生成方法
下面的公式截图也来自这篇论文
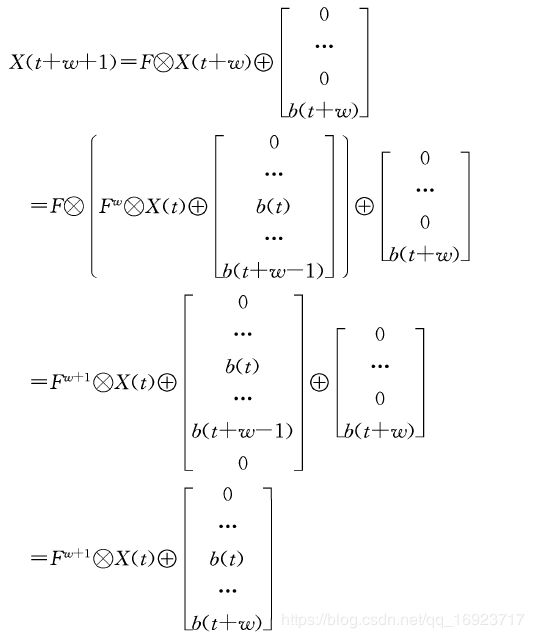
单bit实现,从 x ( t ) x(t) x(t)到 x ( t + 1 ) x(t+1) x(t+1), ( x 0 , x 1 , … , x m − 1 ) (x_0, x_1, …, x_{m-1}) (x0,x1,…,xm−1)是当前要与被除数 p o l y poly poly: ( p 0 , p 1 , … , p m − 1 , p m ) (p_0, p_1, …, p_{m-1}, p_m) (p0,p1,…,pm−1,pm)相异或的数据, b ( t ) b(t) b(t)是刚进入的新的bit。
既然写出了 x ( t ) x(t) x(t)到 x ( t + 1 ) x(t+1) x(t+1)的关系,那么 x ( t ) x(t) x(t)到 x ( t + w + 1 ) x(t+w+1) x(t+w+1)的关系也能写出来,这样我们就能一次实现 w + 1 w+1 w+1个bit的CRC计算。设 F F F等于中间带 p p p的那个矩阵
多bit实现,从 x ( t ) x(t) x(t)到 x ( t + w + 1 ) x(t+w+1) x(t+w+1)
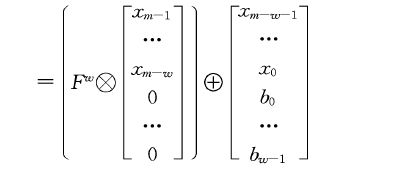
还可以变形成这样,从 x ( t ) x(t) x(t)到 x ( t + w ) x(t+w) x(t+w)
下面的仿真就是后面这种变形,具体推导请查看论文吧,注意这是二进制的矩阵运算。
2.3 并行矩阵生成
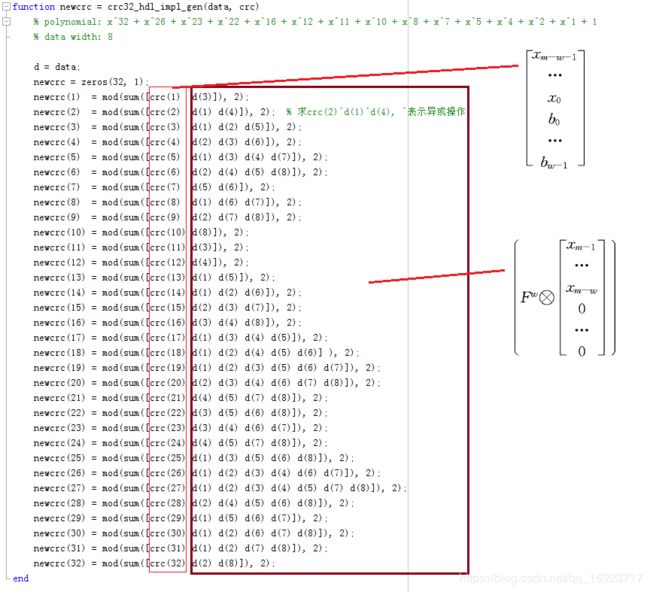
( p 0 , p 1 , … , p m − 1 , p m ) (p_0, p_1, …, p_{m-1}, p_m) (p0,p1,…,pm−1,pm)我们是知道的,这样就可以先算出 F w F^w Fw,然后根据输入的数据 ( b w − 1 , . . . , b 0 , x 0 , x m − w − 1 , x m − w , . . . , x m − 1 ) (b_{w-1}, ..., b_0, x_0, x_{m-w-1}, x_{m-w}, ..., x_{m-1}) (bw−1,...,b0,x0,xm−w−1,xm−w,...,xm−1)直接一次性完成 w w wbit位宽的CRC计算。
下面是用MATLAB算出的 F w F^w Fw,省略了后面的24列,因为公式中第一步要乘的矩阵后面24行全为0。
参数:
P O L Y N O M I A L = ′ 04 C 11 D B 7 ′ ; POLYNOMIAL = '04C11DB7'; POLYNOMIAL=′04C11DB7′;
W I D T H = 8 WIDTH = 8 WIDTH=8
2.4 MATLAB仿真及验证
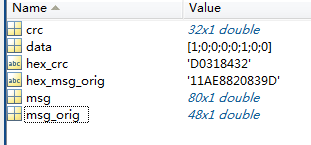
有了 F w F^w Fw就可以完成HDL的编写了,不过这里没有去写,只是用MATLAB模拟了下,如图所示
添加主程序进行仿真,将得到的数据与在线验证网站对比
http://www.ip33.com/crc.html
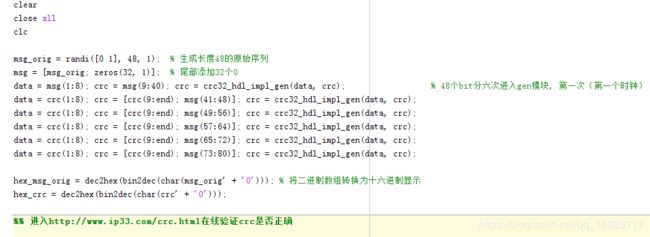
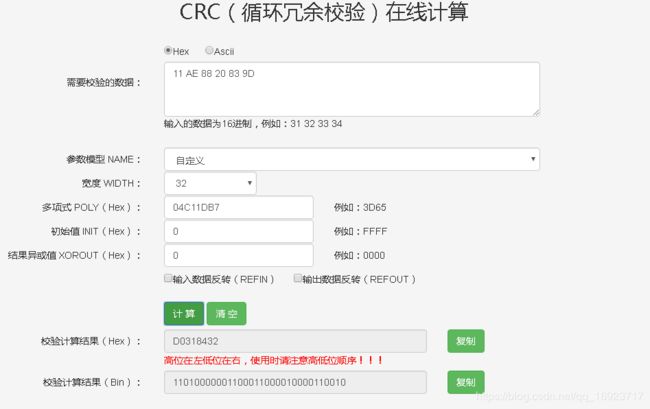
可以看到结果是对的
https://crccalc.com/也可以验证,但是因为不能自定义,所以不能得到本文仿真一样的结果。
4 总结
可以看到,其实CRC的实现方式是很固定的,所以就可以通过Python或者MATLAB的文本处理自动生成任意位宽,任意多项式的Verilog/VHDL代码,而且这样的在线网站也是有的
http://www.easics.com/webtools/crctool(这个好像失效了)
http://outputlogic.com/?page_id=321
MATLAB仿真代码在这里
没分的可以在评论里留下邮箱,记得先点赞^_^
20190812更新
上面的思路是 x ( t ) x(t) x(t)到 x ( t + w ) x(t+w) x(t+w)的公式推导,今天看到另一个思路:
单比特实现是线性移位寄存器每次移位一次实现,那么如果能一次移位8个,就能一次输出8bit的结果,但是移位寄存器是不可能在一个时钟周期内移8位的,所以这部分电路用组合逻辑完成。感觉这个思路理解和实现起来更简单些。
.
.
.
.
.