多项式题单

LOJ #556. 「Antileaf’s Round」咱们去烧菜吧

求混合背包（某一体积的物品可能有无限个也可能有有限个），得到体积和为$1...n$的方案数。

热身题。
如果一个体积为$v$的物品有无限个，那么其关于体积的普通生成函数为${\sum }_{i=0}{x}^{vi}=\frac{1}{1-x^v}$
如果一个体积为$v$的物品有$K$个，那么其关于体积的普通生成函数为${\sum }_{i=0}^K{x}^{vi}=\frac{1-x^{v(K+1)}}{1-x^v}$
将这些生成函数乘起来即可得到答案的生成函数。
发现总项数可能达到$n^2$不能直接上多项式乘法，可以考虑对每个式子取$\ln$求和后求$\exp$。
$\ln (1-x)$泰勒展开可以得到为${\sum }_{i=1}\frac{-x^i}{i}$
所以对于$\ln \frac{1}{1-x^v}=-\ln 1-x^v={\sum }_{i=1}\frac{x^{iv}}{i}$
$\ln \frac{1-x^{v(K+1)}}{1-x^v}={\sum }_{i=1}\frac{x^{iv}}{i}-{\sum }_{i=1}\frac{x^{iv(K+1)}}{i}$
求出$x^{iv}$中$v=v_0$的系数和后即可$O(n\ln n)$求和得到$\ln$后的式子求和的生成函数。
代码

LOJ #6055. 「from CommonAnts」一道数学题 加强版

社论
$$f_k(x)=\sum _{i=1}^{x-1}{f}_k(i)+x^k,f_k(1)=1$$
这个式子是一个 $n$阶递推，既不是齐次也不是线性。
我们可以化一下式子变成常系数非齐次线性递推。
$$\begin{gathered} f_k(x)=f_k(x-1)+(\sum _{i=1}^{x-2}{f}_k(i)+(x-1{)}^k)+x^k-(x-1{)}^k \\ =2f_k(x-1)+x^k-(x-1{)}^k \end{gathered}$$
这是个一阶常系数非齐次线性递推。
我们知道如果是齐次的话，因为这个递推式只有一阶，第$n$项可以用递推式的特征根的$n$次方之类用快速幂解决。
变成齐次的方法很简单，
构造递推式$g_k(x)=2g_k(x-1)-x^k+(x-1{)}^k$
所以$(f_k(x)+g_k(x))=2(f_k(x-1)+g_k(x-1))$。
我们求的$f_k(x)=2^{x-1}(f_k(1)+g_k(1))-g_k(n)$
考虑到我们需要的$g_k(x)$只需要满足一个递推式，发现有且仅有一个$k-1$次多项式$g_k(x)$满足这个方程。
也就是说$g_k(x)$可以是一个$k-1$次多项式。
那么我们只需要求出$g_k(0...k-1)$即可拉格朗日插值得到$g_k(n)$，从而算出$f_k(n)$。
分别求出 $0...k$的$k$次方后，可以通过假设$g_k(0)$递推得到$g_k(k)$，然后通过拉格朗日插值得到$g_k(k)$的另一个表达式，解出$g_k(0)$即可。

Code

LOJ #6391. 「THUPC2018」淘米神的树 / Tommy

社论
容易发现这个顺序其实类似于树的拓扑序反过来。
当两个初始点重合的时候就是求树的拓扑序计数。
经典结论：答案为$\frac{n!}{{\prod }_{iintree}s{z}_i}$，其中$s{z}_i$是以初始黑点为根时$i$的子树的大小。
当两个初始点不重合时，新建一个点$s$，将初始点和$s$连边。
那么我们将会得到一颗基环树，枚举环上的一条边割掉，我们就可以把问题看做以$s$为初始黑点求树的拓扑序计数。
考虑割掉的这条边，它左右两边的点中一定恰好有一个是环上最后一个被染成红色的点，所以对于一种情况有两种可能的割边（最后一个被染成红色的点左右有两条边），所以最后答案要$÷2$。

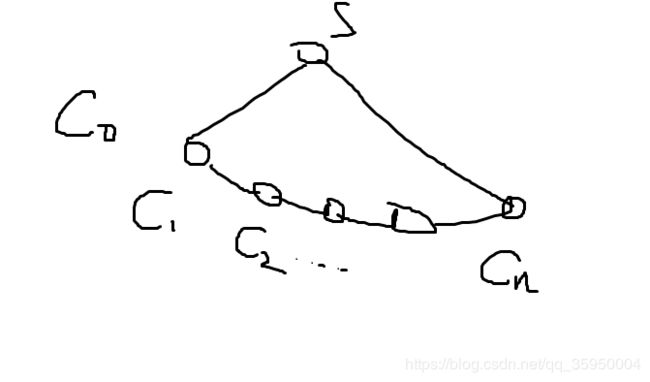
然后在两个初始黑点中选一个为根求出每个点的子树大小，其中两个初始黑点间的链的每个点的子树大小依次记为$c_1,c_2...c_n$，再在左边加一个$c_0=0$，注意这里$c_1...c_n$是递增的。
那么$|c_i-c_j|$在$i>j$时的意义就是在$j\to j+1$这条链断开时的$i$的子树大小。
在$i<j$时的意义就是在$j\to j+1$这条链断开时的$i+1$的子树大小。
所以在断开$j\to j+1$时的链上的$\prod sz={\prod }_{i!=j}|c_i-c_j|$，不在链上的预处理即可。
那么我们只需要求${\sum }_j\frac{1}{{\prod }_{i!=j}|c_i-c_j|}$，发现这个东西和多项式快速插值的第一部分一模一样。
具体的设$F(x)={\prod }_j|x-c_j|$，有${\prod }_{i!=j}|c_i-c_j|={\frac{F(x)}{x-c_i}|}_{x=c_i}$
因为$F(c_i)=(c_i-c_i)=0$用洛必达法则，有：
${\prod }_{i!=j}|c_i-c_j|=F(c_i{)}^{\prime }$
分治 $FFT$后求导套多点求值即可。

Code

LOJ #6609. 无意识的石子堆 加强版

社论

容斥做法：
枚举有具体$k$列放了两颗石子，具体的$2n-2k$列放了一颗石子的方案数为$S_k$。
$$ans=\sum _{k=0}^n\left(\genfrac{}{}{0ex}{}{m}{k}\right)\left(\genfrac{}{}{0ex}{}{m-k}{2n-2k}\right)S_k$$
求$S_k$，考虑容斥掉同一行的两颗石子不能在同一列这个限制。
$$S_k=\frac{1}{2^{n+k}}\sum _{i=0}^k\left(\genfrac{}{}{0ex}{}{n}{i}\right)\left(\genfrac{}{}{0ex}{}{k}{i}\right)(-1{)}^{i}i!2^i(2n-2i)!$$
这里枚举的$i$是同一行的两颗石子在同一列的次数。
统计时将同一行的两个石子看做不同，放在同一列的两个石子先后有顺序，这样统计$2n-2i$个石子放入剩下还空着的列时可以直接写$(2n-2i)!$，相对应的需要在外面$÷2^n÷2^k$（有$k$列可以放两个石子）。
$i!$表示这$i$行都分别有两个重合的石子，将他们分配给$i$列的方案，$2^i$是因为这两个石子之间有顺序。
$$S_k=\frac{n!k!}{2^{n+k}}\sum _{i=0}^k\frac{1}{(k-i)!}\frac{(-2{)}^i(2n-2i)!}{i!(n-i)!}$$
就可以卷积求出$S_k$，然后直接求得答案了。
还有一种多项式$exp$但是不写$exp$的推法，本质应该有点类似，具体可以看上面的博客。
Code

LOJ #6703. 小 Q 的序列

社论
$dp1:f_{i,j}=f_{i-1,j}+f_{i-1,j-1}(a_i+j)$，$f_{i,j}$表示前$i$个数选了$j$数的贡献和。
发现这个$dp$我不太会做。
换一下定义：$f_{i,j}$表示前$i$个数选了$i-j$个数的贡献和。
$dp2:f_{i,j}=f_{i-1,j-1}+f_{i-1,j}(a_i+i-j)=f_{i-1,j-1}-j{f}_{i-1,j}+f_{i-1,j}(a_i+i)$
考虑组合意义（和第二类斯特林数相似）：对于每个$i$我们有三种选择，
不选，代价$\times (a_i+i)$,
选，加入前面$j$个组中的一个，代价$\times (-j)$，
选，新建一个组，代价无变化。
不选$i$个的代价可以用分治$FFT$求${\prod }_{i=1}^n(x+a_i+i)$
选$i$个的代价，可以先考虑选一组的指数生成函数是$-(e^{-x}-1)$，$(e^x-1)$是非空集合带标号的指数生成函数，我们这里除了第一个数，别的数加入还需要$\times -1$，所以是$-(e^{-x}-1)$。
那么选 $i$个的代价的生成函数就是$\exp (1-e^{-x})$，注意是指数生成函数还需要除阶乘。
然后将选和不选的生成函数卷积一下求$x^n$项即可。
Code

LOJ #6247. 九个太阳

福利题快速幂模板题

单位根反演：$\frac{1}{k}{\sum }_{i=0}^{k-1}{w}_k^{ij}=[k|j]$
当$w_k^j=1$时，即$[k|j]$时，原式$=\frac{k}{k}=1$
否则原式$=\frac{1-w_k^{kj}}{k(1-w_k^j)}=0$

所以对于此题：${\sum }_{i=0}^n[k|i](\genfrac{}{}{0ex}{}{n}{i})=\frac{1}{k}{\sum }_{i=0}^n{\sum }_{j=0}^{k-1}{w}_k^{ij}(\genfrac{}{}{0ex}{}{n}{i})$
$=\frac{1}{k}{\sum }_{j=0}^{k-1}{\sum }_{i=0}^n{w}_k^{ij}\left(\genfrac{}{}{0ex}{}{n}{i}\right)=\frac{1}{k}{\sum }_{j=0}^{k-1}(1+w_k^j{)}^n$
此题模数很友好，求出单位根后快速幂即可。
Code

LOJ #6289. 花朵

设$f_{u,i,0/1}$表示$u$子树内选了$i$个点，其中$u$选没选为第三维的答案，
那么树链剖分后建出全局平衡二叉树，对于虚儿子到父亲的转移即为$f_u$的分治$FFT$。
对于重儿子到父亲，对重链分治，对于每一边求出$g_{i,0/1,0/1}$表示重链的某部分即下方的虚子树，头是否被选为第二维，尾是否被选为第三维。

对重链分治的时候可以按照下面子树的$sz$分治而非对半分治，可以优化常数。
$O(n{\log }^{3}n)$很好证明。

但是有人说这样写是$O(n{\log }^{2}n)$的
Code

LOJ #6363. 「地底蔷薇」

$F(x)={\sum }_{i=0}\frac{2^{\left(\genfrac{}{}{0ex}{}{i}{2}\right)}{x}^i}{i!}$有标号无向图数量。
$D(x)=\vartheta \ln F(x)=[\ln F(x{)}^{\prime }]x$即有根有标号联通无向图数量。
$B(x)={\sum }_{i=1}\frac{b_{i+1}{x}^i}{i!}$，$b_i$为$i$个点的无根有标号点双连通图数量。
那么一个有根有标号联通无向图的根节点周围可以挂若干个包含根的点双，挂一个大小为$i+1$的点双，那么除了根以外的$i$个点，每个点删去和该点双其他点的连边后的连通块是一个有根有标号联通无向图。
$D(x)=x\exp [{\sum }_{i=1}\frac{b_{i+1}D(x{)}^i}{i!}]=x\exp B[D(x)]$
假设$G[D(x)]=x$即他们互为复合逆。
那么$D(G(x))=G(x)\exp B[D(G(x))]$
也即：$x=G(x)\exp B(x)$
$B(x)=\ln \frac{x}{G(x)}$
令$\ln \frac{D(x)}{x}=C(x)$
则有$C(G(x))=\ln \frac{x}{G(x)}=B(x)$
又根据扩展拉格朗日反演可以得到：
$[x^n]B(x)=[x^n]C(G(x))=[x^{n-1}]\frac{C(x{)}^{\prime }{x}^n}{nD(x{)}^n}=[x^{n-1}]\frac{C(x{)}^{\prime }}{n}\times (\frac{x}{D(x)}{)}^n=[x^{n-1}]\frac{C(x{)}^{\prime }}{n}\exp (-n\ln \frac{D(x)}{x})=[x^{n-1}]\frac{C(x{)}^{\prime }\exp (-nC(x))}{n}$
首先可以看到

发现这个条件让你可以直接多次拉格朗日反演求出大小$\in S$的所有点双连通图的方案数，设他的生成函数为$C(x)$。
然后和点双联通图计数一样的方法设答案为$F(x)$。
那么考虑包含根的点双，把这些点双的边删掉之后，所有的点都可以挂一个我们正在求的图也即$F(x)$，然后自由组合。
所以可以得到方程：
$F(x)=x\exp C(F(x))$
发现有：
$\frac{F(x)}{\exp C(F(x))}=x$
所以$F(x)$和$\frac{x}{\exp C(x)}$互为复合逆。
$[x^n]F(x)=[x^{n-1}]\frac{x^n}{n\frac{x^n}{\exp C(x{)}^n}}=[x^{n-1}]\frac{\exp nC(x)}{n}$
Code

AtCoder - agc005_f Many Easy Problems

题意：对于$k=1...n$，求在树上选$k$个点的所有方案中，在这$k$个点中某两个点的最短路径上的点数。
发现对于选$k$个点，答案是一个连通块，所以边数$=$点数$-1$，所以我们计算总边数最后加上$\left(\genfrac{}{}{0ex}{}{n}{k}\right)$即可。
对于一条边$(a,b)$，它在这个连通块内即代表这$k$个点不在同一边，假设一边的大小为$sz$，则它在这个连通块内的方案数为$\left(\genfrac{}{}{0ex}{}{n}{k}\right)-\left(\genfrac{}{}{0ex}{}{sz}{k}\right)-\left(\genfrac{}{}{0ex}{}{n-sz}{k}\right)$
将组合数拆开$k!\times \left(\genfrac{}{}{0ex}{}{sz}{k}\right)=\frac{sz!}{(sz-k)!}$
做一下差卷积即可将$\left(\genfrac{}{}{0ex}{}{sz}{k}\right)$贡献到每个$k$。

Code

Codeforces 1096G Lucky Tickets

0~9种有k种可用数字，求前n/2个数字和与后n/2个数字和相等的方案数
对一个最高次数为$9$的多项式求它的$10^5$次幂即可。
可以直接做$1e6$的$NTT$然后把每个点值快速幂后再$NTT$回来即可。
也可以通过$g=f^k,g^{\prime }=k{f}^{k-1}{f}^{\prime }$得到$g^{\prime }f=kg{f}^{\prime }$
$n{g}_n{f}_0={\sum }_{i=1}^{9}ki{f}_i{g}_{n-i}-{\sum }_{i=1}^9(n-i)f_i{g}_{n-i}$,$f_0=0$可以通过平移多项式解决。
从而$O(81n)$得到$g=f^k$。