CoNEXT 2019 Network topology design at 27,000 km/hour 论文翻译与分析

引用：
Bhattacherjee D, Singla A. Network topology design at 27,000 km/hour[C]//Proceedings of the 15th International Conference on Emerging Networking Experiments And Technologies. 2019: 341-354.
通过本文得到的知识与数据：

学习到的知识与数据：

1. 截至2019年6月：
   Starlink（SpaceX）：计划部署超过一万二千颗卫星，其中在部署过程中的有4425颗，第一个平面包括24轨道每个轨道66颗卫星共1584颗卫星，轨道倾角53°海拔550km。LEO以外还计划部署7518颗VLEO（非常低轨），海拔在340km左右
   Kuiper（Amazon）：目标是建设3236颗LEO卫星，分为三个阶段。A为$34^2$星座，倾角51.9°，海拔630km；B为$36^2$星座，倾角42°，海拔610km，C为$28^2$星座，倾角33°，海拔590km
2. geodesic distance 测地距离，两点之间经过一个平面的最短距离，比如球体上两点的测地距离需要经过球表面
3. 即使十多年前，超过4900km的5.6Gbps的星间激光链路就已经实现了。最近在相距45000km的GEO和LEO之间高速传播数据也已经实现。因此本文使用的ISL容量为数十Gbps。对于ISL建立时间，可能是几秒到几十秒之间，取决于很复杂的原因。读者仿真的时候可以借鉴其相关文献。
4. 可见性限制的原因及具体数据:
   主要目的是防止星间链路经过热大气层。这是大气层中最低的一层，缺乏水汽，起于地表80km。因此，ISL间隙不能低于80km。可以计算对550km高度来说，最大的ISL长度是5014km。这个范围限制了ISL只能建立在相邻的或同一个轨道以内。但对于更密集的星座来说，则会有很多可能性。比如，对于550km的53°倾斜轨道的$40^2$星座来说，一颗在赤道的卫星的可能建连的候选集可达到190颗
5. LEO相较于地面提供低时延网络的优势：更短的路径、相较于光纤更接近于光速
6. 文中模拟了当今因特网城市间的RTT以及使用LEO以后的RTT，发现大部分RTT提升可达到70%左右
7. 对更少的跳数就能实现更低的拥塞进行了论证和实验验证。直觉上，端点间跳数越少，意味着一个连接会占用的整体容量越少。而本文的验证中也通过数据验证了这一点
8. 对不同拓扑优势比方案：本文对比的参数可以是对网络的端对端的距离拉伸程度、跳数变化以及二者的结合

本文方案的简介：

• LEO拓扑设计相对于基础图论问题的不同：
  1. ISL受限于空间距离，而图论的抽象中往往不加入位置条件
  2. 星间和星地的相对运动使得候选连接集处于不停的变化之中
• 将静态LEO网络的拓扑规划可以简化为一个数学问题：
  已知一个星座的卫星位置以及每个卫星有限的星间连接装置，并给出地面目标端点之间的流量矩阵，在可见性限制条件下，如何建立卫星间连接来实现最小延迟路径。
  文中给出三种传统方案
  1. 整数规划。由于问题规模庞大，有限的计算能力仅能计算得到25个城市的结果，对于一个1000城市的运行中的系统，需要$10^{29}$天。且此规划完全不考虑动态性，导致不同时间算出来的结果相似性很差，动态变化剧烈
  2. 随机图。动态性问题依然明显，且无法根据当前流量变化进行适应性变化
  3. 蚁群优化。同样有计算复杂度过高的问题
• 本文方案设计与优化：
  1. 基础方案是将原有的全局拓扑设计问题简化为单点设计，即每个卫星的本地视图作为一个模型，使所有的卫星重复这个模型。（一个motif就是一个3颗卫星、2条ISL连接的模式，在整个星座中重复）
  2. 基于纬度不同星间距离不同候选集也不同的前提下，为不同纬度卫星设计不同主题
  3. 方案能保持较长时间的星间链路不变性，防止了频繁、昂贵的网络变化
  4. 方案结果：最优motif相对于网格对M1，M5和M10的提升中值(95%值)分别是44.5%(54%)、26.2%(37%)和16.8%(22.3%)
• 文章认为，想要获得一个低延迟的LEO网络，星间建立链路是必然的，否则对于长距离的网络而言，这个连接必然会因为没有星间链路需要在星地之间来回跳动造成高延迟，并间接造成网络容量的降低
• 如何根据全球的人口分布设计一个合理的流量模型
  本文方案是对两个城市之间的流量，使用两个城市的人口乘积作为流量映射在[0,1]区间的权重
• 文中一直提到的网络效益究竟是如何评估的，是否具有可借鉴性
  本文的收益评估方案比较简单，仅考虑在相应的拓扑下的任意两个端之间的拉伸和跳数来评判这个拓扑的优劣，同时还讨论了跳数与链路利用率的关系，间接展示了拓扑的拥塞性。对影响拓扑方案结果的各个参数，如卫星规模、倾角、度量比例进行了讨论

如果以上内容有比较感兴趣的，可以继续下面的详细阅读。
翻译+个人理解

摘要

大量空间公司积极制造各种低轨卫星星座来提供全球互联网服务。我们发现了低延迟高容量的卫星间网络设计的问题。假定这种高密度高速星座让传统网络设计方案失效，因此需要为这个新的问题集寻找新的方案。

我们提出一种方案，直接面向处理低轨卫星的高时间动态问题。我们利用网络拓扑中重复的模式来防止随着时间变化带来的昂贵的链路变化，并保证提供相对于以前标准方案的接近最小的时延和接近2倍的吞吐。除此之外，我们发现，如果允许一小部分的链路动态变化，那么卫星星座的拓扑将会允许更多更有效的设计。对于Starlink，我们的方案能够提升54%的效用

1 引入

网络基础设施可能处于一场根本改变的风口浪尖。SpaceX提出接近一万二颗卫星的Starlink星座当第一次发射成功60个测试卫星后，吸引了公众的想象力，但它只是新的一场建设基于卫星的网络服务的太空竞赛。大量的处于不同成熟阶段的竞争项目使得它看起来下个年代将要提供消费者服务

面向消费者的卫星网络已经存在了数十年，而新出现的这些与以前的那些在目标、规模以及技术上都有不同。大规模的“新空间”星座目标是便宜的、世界范围低时延的网络，覆盖了上千个低轨卫星。Starlink宣称的目标甚至是承载大部分的互联网长途流量。相反的，最近部署的星座如HughesNet使用数十颗GEO为农村地区提供利基服务，最多只能接入几千万用户，且造成了几百ms的大延迟。铱星和铱星NEXT瞄准的是更狭窄的卫星电话市场。很多新提出的大型星座更宏大的目标是提供一些看似合理的先进技术，包括使用可重复使用的火箭廉价进入轨道，使卫星小型化，以及使卫星之间能够相互快速移动的卫星与地面站之间能够连接的链路跟踪技术。

既然LEO卫星提供互联网是必然的，让我们来研究它们的网络设计。最近的工作表示，即使适当的考虑了端到端系统中的瓶颈部分，比如星地连接，提升星间网络的容量依旧能充分提升地面站之间的吞吐。然而，这个工作重点在于使用高耗费的星间连接作为载体提升星间连接，忽略了通过更好的网络设计来代替。这个方法接受了现在的一种暗示，它们认为星间连接必须要与相邻的卫星形成格状的连接，即：每个方向连接最近的一颗卫星，和以前更小型的卫星星座一样。现有的专利、可视化和分析都符合这个假设。但这个假设是没必要的且有限制的：很多时候，连接更远的卫星是可能的，更长的连接能提升网络的吞吐效率，因为这样会让端到端的连接使用更少的、更长的星间跳数。

允许更长的连接能极大提升设计空间，也会让拓扑设计成为一个高难度的问题：已知一个卫星允许一个小数量的星间连接，它们如何连接能最大化网络带宽并最小化延迟？据我们所知，这个问题，不要说解法了，它在最优化领域中就没有被提出过，至少在大型星座的背景下。

这个问题看似是个传统的网络优化问题，非常像是类似于数据中心提出的问题，在那里有很长基于图论的的交换机间连接的研究历史。然而，相对于其完善的学习集，这里有两个不同的设计条件：

• ①星间链路（ISL）受限于范围，只有附近的卫星可以相互连接
• ②星间及星地在相对移动。

前者提出的挑战是图论的抽象通常不加入位置条件，而后者需要加入额外的考虑，即随着与地面节点距离变化，可行连接集也会发生变化。即使在简单、静态条件下网络设计也是NP难的，那我们该如何处理临时性变化带来的复杂性呢？

我们提出了一个具体的例子，直观展示了网络设计方法从传统的设置经验是不适合这种新的，非传统的问题背景的。我们的研究表明，即使有大量的特定问题自定义，整数线性规划、随机图和蚁群优化等方法仍然不能满足要求。

作为尝试定位问题的第一步，我们提出了一个创新的方法，这个方法利用了重复的模式：如果拓扑受到限制使得每个卫星的本地视图和任意其他卫星相同，那么可以将拓扑设计限制在一颗卫星上所有可能的局部视图空间。我们把每个这样的本地视图叫做一个motif。这个motif在所有卫星之间重复，通过相同的方式与邻居连接。motif设计的尽管也不简单，但已经足够小能够穷尽列举并为目标motif流量矩阵找到最优了。

使用上述简单方法就已经能提供一个相对于邻网格基线的2倍效益的提升了，我们又发现卫星在高纬度时星间距离会更近，因此可能的连接集也会更大。因此，在不同纬度的motif可以又不同的规范，这样能进一步提升网络容量。即使我们对功率有限的ISLs的范围做了最坏的假设，这种方案也能提高效率——对starlink，使用我们的方案，即使在最坏的情况下，使用我们的方法也能相对于邻网格提升37%。

我们同样展示了我们的方法有效的处理了LEO固有的随时间变化的问题：基于motif的ISL会保持长时间阶段，因此防止了频繁、昂贵的网络连接变化。

我们在最后指出了一些初期研究空间中的不确定性。因此，通过考虑可能产生影响的技术选择的几个潜在结果，我们对问题设置采取了一个广泛的视角。我们认为，这种方法比放弃影响尚未开发的卫星星座设计的机会更好，如果我们等待更大的清晰度，狭窄的设计窗口可能会关闭。

我们有下面的这些贡献：

1. 我们为LEO星间拓扑设计问题给出了一个框架，展示了为什么一些直觉上的方案不适合解决这个问题，那些方案包括：整数规划、随机图、蚁群优化等
2. 我们提出了一种新的设计这类网络的方案，使用了规律性的重复模式，即：motif
3. 我们展示了LEO星座空间几何如何让定制的motif应用到拓扑的不同地方
4. 我们研究了允许的ISL的范围的影响及设置时间的有效性对我们方法的影响
5. 我们在目前提出的两个最大的星座starlink和kuiper上进行了模拟，展示了我们的方法相对于邻网格化的连接分别有了54%和45%的优化，模拟中的数据使基于一个自然的、人口加权的流量模型
6. 对starlink，我们发现即使使用ISL的范围的消极假设，网络性能也能提升40%
7. 文中的数据和代码都是公开的

期望在阅读完本文后可以学习到的东西：
1. 如何根据全球的人口分布设计一个合理的流量模型
2. 分别使用整数规划、随机图、蚁群优化等方案是如何应用到拓扑设计中的
3. 文中一直提到的网络效益究竟是如何评估的，是否具有可借鉴性
4. 是否有比较通用的网络拓扑设计复杂性评估的材料可以借鉴
希望在阅读完成本文以后能有以上收获

除了我们具体的方法和结果，我们希望我们在这个特定的问题和约束条件上的讨论，以及我们对它们战胜传统方法的分析，能帮助在这个领域的研究建设出行，就行一些数据中心网络设计的初期工作一样。

2 背景

考虑到非典型的问题设置，我们提供了关键方面的背景知识，这可能有助于我们的网络受众。

2.1 卫星轨道和星座

完全描述轨道信息需要7个参数，但所有的星座都提供了较少的参数，因此我们下面只进行简单的介绍：

1. 倾角（inclination）：轨道与赤道之间的夹角。极地轨道的倾角是90°，更小倾角的轨道不经过几点，在低纬度花更长时间。无论极地轨道还是非极地轨道，卫星密度在远离赤道的方向上增加
2. 高度（altitude）：测量的是海平面高度，并决定了轨道速度。GEO卫星必须在24小时完成一圈，其轨道高度为35786km。LEO卫星低于2000km。低于600km高度的轨道能在100min内完成绕地球一周
3. 相移（phase shifts）：表示卫星间的相对位置。连续的轨道经过赤道的不同点。如果相移是均一的，30个轨道时轨间相对位置是12°；同理，如果每个轨道平面有20颗卫星，同一平面连续卫星之间的相移为18°。所有已经提出的卫星星座都是均匀分布的，所以，简单起见，会使用轨道数p和轨道内卫星数n来代替，称p=n的星座为n^2星座

现已有很多新的卫星星座被提出用于提供全球性的网络宽带服务，包括starlink、Kuiper、OneWeb、Telsat、LeoSat和Hongyan。本文只讨论其中最大的两个。

1. Starlink（SpaceX）：计划部署超过一万二千颗卫星，其中在部署过程中的有4425颗，第一个平面包括24轨道每个轨道66颗卫星共1584颗卫星，轨道倾角53°海拔550km。LEO以外还计划部署7518颗VLEO（非常低轨），海拔在340km左右
2. Kuiper（Amazon）：目标是建设3236颗LEO卫星，分为三个阶段。A为$34^2$星座，倾角51.9°，海拔630km；B为$36^2$星座，倾角42°，海拔610km，C为$28^2$星座，倾角33°，海拔590km

这些都是配合着不断发展的部署策略在不断变化的状态中。我们基于它们截止到2019年6月的已发表的信息文件

2.2 系统动态性

从GEO到LEO降低了延迟，但让星座处于高度动态中。550km的海拔让星座的运动速度在27306kmph，在一分钟内覆盖的距离大约是慕尼黑-柏林，德里-拉合尔，或者圣约瑟-洛杉矶之间。在赤道周围时，同一轨道高度及倾角的相邻或附近的卫星的相对速度很小，但在高纬度的相对位移很大。因此，哪些卫星之间互联以及连接到地站都是随时间变化的。卫星间距离、相对速度，以及我们使用的技术，决定了哪种连接时合适的以及这种连接的建立需要多久

2.3 连接

星间、星地都会进行互联。我们讨论的重点是星间连接，并限制对星地的连接的要求是必须在可见范围内。基于卫星的位置，地站只有在卫星所处的圆锥形下时才能接入到卫星，且随着卫星高度提升，卫星的覆盖变大

LEO网络对低延迟高容量的需求使得星间链路成为必然，否则长距离的连接必将造成星地之间来回的传播，造成大时延，且降低网络容量

ISL受限于可见性和功率，在较小程度上，还会受限于无线电或激光对准快速移动的卫星，并补偿多普勒偏移和前方点角度，快速建立卫星之间的联系的能力。然而，即使十多年前，超过4900km的5.6Gbps的星间激光链路就已经实现了。最近在相距45000km的GEO和LEO之间高速传播数据也已经实现。因此，推测ISL容量可达到数十Gbps是可行的。ISL的链接建立时间在几秒到几十秒间，取决于相对位移和建立方式

已有的非GEO星座如铱星使用网状方案设计他们的星间链路，并论证了工程可行性和科学性：每颗卫星有四个方向的ISL，连接到最近的4个邻居，2个是同轨道的，2个是邻居轨道的。这样的链接可以保持很长时间，且相连的卫星有很低的相对速度（高纬度以外）。这种连接方式的微小变化变种也是可行的，比如，相邻轨道是同向或反向的。简单起见，我们称这种连接模式是网状的

通用的假设是新的星座也会使用同样的方法，这反映在可视化和一些星座的设计上。但我们使用一个简单的计算来张明这种观点并不是需要严格遵守的

可见性限制的主要目的是防止星间链路经过热大气层。这是大气层中最低的一层，缺乏水汽，起于地表80km。因此，ISL间隙不能低于80km。可以计算对550km高度来说，最大的ISL长度是5014km。

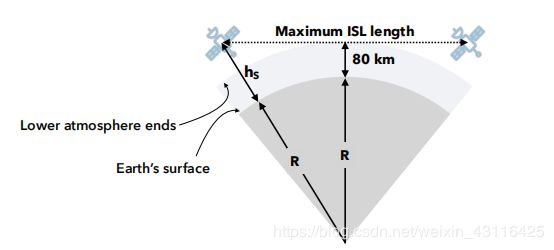
对有数十颗卫星的小型星座来说，这个范围限制了ISL只能建立在相邻的或同一个轨道以内。但对于更密集的星座来说，则会有很多可能性。比如，对于550km的53°倾斜轨道的$40^2$星座来说，一颗在赤道的卫星的可能建连的候选集可达到190颗

当然，除此之外，功率、相关设备的大小和质量也是限制因素。为了固定所需的链路特性，较长的距离需要更多的传输功率，以及更大更重的设备，这将会让卫星系统更加贵重。因此，除了可见性限制外，我们也分析了受限于其他原因的限制范围

2.4 基于卫星的网络的目标

已提出的星座的目标是扩展覆盖区域到边远地区，以及提供比地面时延更低的网络。对于长距离链接能提供更低时延的可能性体现在：

• ①相对于地面与会的光纤路线，能够提供接近最短路径（在增加了上下链路的开销后）
• ②以光速c而不是光纤内的速度2c/3传播。

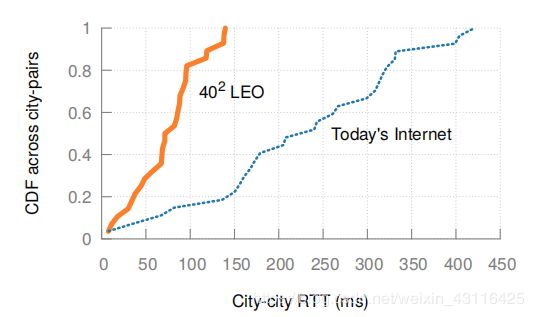
我们对比了人口最密集的城市的当前的通信和基于$40^2$的类Starlink LEO星座通信的RTT，使用WonderNetwork ping statistics进行了当前8个最密集城市之间的时延统计，并模拟了卫星网络，使用networkx提供的网格配置，通过ISL最短路径路由算法计算。可以发现，大部分RTT提升都达到70%。这个比较对卫星网络来说似乎过于有利：次优路由、拥塞排队和前向纠错在这里都没有被计入，而WonderNetwork的数据都已经计入了。然而，这些开销相较于数百ms的RTT不同而言好像变得微不足道，尤其星座设计就是面向低时延的。

将这种延迟优势提供给大量的全球通信量，还需要对每个卫星有限的ISL数量和容量进行使用，以便星座实现高吞吐量。我们使用卫星跳数作为卫星吞吐的简单代理，借鉴以前的网络设计工作：一个端对端连接通过多个ISL使用每个ISL的容量，减少其他连接的容量。因此，对于固定的ISL数量、容量，为端对端连接减少跳数能节省带宽，就能让网络为更多流量服务。

更精确的方法可以解决各种可能的路由方案，但会使本来就复杂的问题变得更加困难。除了这种基于可跟踪性的实用理由之外，简化跳转计数在此上下文中产生能力方面也是合理的：考虑到低延迟目标，无论如何，路由都被限制为在端端延迟方面最短或接近最短的路径。为支持这种想法，我们后续会展示，相较于网格连接的多跳路径，我们的拓扑可以在最短路径路由中实现大幅度低的拥塞，大约有90%能达到5倍。

同样，我们对延迟的计算只使用传播延迟而忽略排队和每一跳的计算。当然，计算后两者只会让我们的结果更提升，因为我们比+Grid方案有更少的跳数

总之，ISL必须被选择这样端到端连接才能最小化ISL跳数和延迟。这就产生了我们要解决的网络设计问题

3 典型的网络设计？

已知：

• a 一个星座卫星轨迹
• b 每颗卫星上有少量卫星连接装置
• c 一个地面端点之间的目标流量矩阵

我们的目标是决定怎样建立卫星间连接来建立一个最小延迟的跃点计数的端到端路径

同样网络设计问题中的静态变种（忽略卫星移动和地球自转）是一个NP难问题，但大家会想到一些方法用来有效解决这些问题，方法包括整数规划、线性规划、蚁群优化、随机图等，也有人觉得ISL设计问题成本高昂但是个一次性工作，可以使用超级计算资源来解决。

因此我们探索定制了三种直观上的方法来定位卫星拓扑设计。我们讨论为什么这个技术面对问题复杂度和时间动态为什么注定会失败。我们利用这次讨论来更具体地制定限制和目标

3.1 一个静态快照的ILP（整数规划）

想要通过蛮干解决临时状态的问题，可以将问题简化为一系列短期的静态快照，然后使用整数规划解决。

• 输入：
  L：每颗卫星允许接入的最大ISL
  $v_{ab}$：在当前范围卫星a和b是否互相可见
  $d_{a}b$：卫星a和b之间的直线距离
  H：地面节点之间的流量矩阵

虽然这个方法可以使用随机输入，但为了构建一个合理具体的实例，我们

• 假定：
  a. 根据Starlink的规范性文件，L=4，
  b. $v_{ab}$仅由可见性决定，后续我们会给出其他设定
  c. H以1000个人口最多的城市为节点，城市之间的流量与城市对的人口乘积成正比（后续我们也会使用经济活跃度而非人口来测试一个不同的流量）

我们对星地之间的连接使用一个简单的方案：假定只要地站在卫星的可见范围内，就可以连接到卫星。在我们高人口实例中，我们将这些城市中可能存在的地站数量减少到每个城市只有一个，并使用任意带宽和卫星连接，仅受范围限制。
将地站放置与星地连接共同优化放到未来的工作是考虑到以下原因：
a. 如果用户可以购买并部署地站的话，我们无法确定这些部署方案有多少受控于运营商；
b. 即使ISL地带宽比上下行连接的高得多，瓶颈在星间和星地连接中都有出现；
c. 在研究初期分解这个复杂问题是应当的，分解有先例，比如路由和拓扑设计

• 输出：
  $y_{ab}$：在卫星a和b之间的ISL是否是活跃的
  $x_{ab}^{st}$：端点st之间的路径是否会经过ISLab

• 目标函数：
  最终的输出必须是最小化端点间时延和ISL跳数的组合。对于每对端点，使用stretch(S)衡量时延：经过设计的网络的最短路径的距离/测地距离。使用随机线性组合来聚合S与跳数(B)。$M_{\alpha }=\alpha S+B$，一般取α=1，但后面会改变α值来检测影响
  目标函数：${\Phi }_{\alpha }$取所有端点之间的Mα的和，权值为流量矩阵H。最小化${\Phi }_{\alpha }$意味着最小化每单位流量的系统范围的伸展和跳跃数。

• 约束：
  ISL是复式地
  每颗卫星最多有4个活跃ISL
  ISL只有在可见性满足情况下建立
  只有活跃ISL可以传送流量
  卫星流量守恒
  端点应正确地表示源流或接收流

• 定制ILP：
  主要提升ILP的可扩展性。为降低问题复杂度，使用启发式算法，认为与端点距离过远的卫星不应该承担这两个端点之间的流量。获取两个点S和T之间的通讯路径包括：卫星A和B之间的ISL路径、S和A的最低点之间的距离加T和B的最低点之间的距离。如果这个假定的路径超过了S-T之间的距离的1.5倍，就不再考虑这条路径。后续时延会证明这不会影响优化

• 结果：
  使用$40^2$的LEO卫星星座（53°，550km），限制最大ISL距离为5014km。生成的线性规划算法分别计算不同规模的城市。对小规模城市的计算时间尚能接受，几分钟到几天，然后给出最优解。对20个城市，生成的一个网络比网格化网络优化54%

问题1：规模限制。25个城市需要在一个64核500GB的机器上计算超过两天，那么对于一个1000城市的运行中的系统，需要$10^{29}$天

问题2：时间动态性。LEO几分钟内能运行几百千米，因此需要生成非常不同的ISL选择结果。如，对20个城市，一分钟ISL变化仅有9%的ISL共用，即使计算仅需要几秒，这个问题也不具有可扩展性

3.2 随机图

受Jellyfish启发，我们也想探索一种通用的结果，让整个网络能在各种负载下正常工作，而不仅仅是对特定的流量，使用随机正则图（RRG），这些图是从目标节点数（卫星）和度数（每颗卫星4个链接）的所有规则图（即所有节点具有相同连接数）的空间中均匀随机抽样的图

• 定制的RRG：
  不同于已经比较完备的标准集，我们并没有一致的RRG样本，即，在一个严格的空间中没有相对于位置信息规律的图。但直觉上这么严格没有必要，我们设计了一个启发式的过程，来采样允许的边界（但不保证均匀抽样）
  算法首先基于可见性列出所有允许的ISL，并随机从这个列表中抽取。只有两颗卫星都有空余连接才能加入ISL，重复直到无法加入新的ISL。此时，如果仅有少量卫星缺连接，停止，否则，移走所有未满的卫星的ISL然后再重新抽样增加

• 结果及挑战：
  随机选择了5000城市对与网格拓扑进行了对比，计算了拉伸、跳数以及M1。在牺牲了11%的拉伸情况下，随机图减少了53%的跳数，M1降低了43%，Φ1降低42%
  

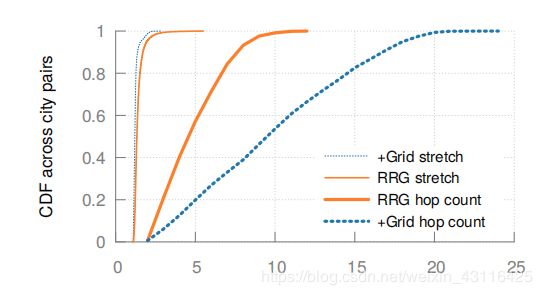
问题1：时间动态性。尽管克服了规模性问题，随机图依旧无法解决时间动态性问题，在2(5)分钟内超过8%(19%)的ISL都不适用。简单的每几分钟就整个改变几乎所有ISL会造成大量的中断。增量改变也不简单，因为一个ISL连接的两个卫星的接口不一定处于同样状态。

问题2：不灵活。不同于线性规划，随机图不会根据一个目标流量矩阵进行特性的优化，也无法像线性规划一样通过α调整两个优化目标的比重，权衡的时候只有一个固定的目标

我们也使用蚁群优化来进行ISL的优化，对数十对城市的小规模问题表现较好，但无法覆盖更大的实例。同样，也会带来高动态扰动。

3.3 挑战总结

对大型星座，必须要考虑进行数千ISL的配置来满足时延和容量目标，同时需要考虑高动态设置。既是对一个静态快照已经很困难了，加上时间动态更加困难。一个理想的解决方案不仅能在静态快照相对于网格设计有较大的提升，还需要降低链路变化的扰动来避免由于链路更改而导致的几秒到几十秒的开销。

4 motifs：简单且有效

前面的工作展示了传统方案的不足，并提出对解法的要求：防止整体的复杂优化和链路扰动。我们需要如同网格一样简单的结构并能获取其他方案一样得收益。我们提出的方案是一个广义的网格。

4.1 使用motif概化网格

对稠密星座，卫星可以与最近的邻居以外的卫星连接。如图所示，A从可连接集中选择了B和C，那么可以在整个网络中重复这种连接模式来获取ISL拓扑。注意，A除了B和C以外的连接都是由其他卫星选择的。因此，所有卫星的本地视图都是完全相同的。这种A选择的模式就是我们所讲的motif。概括来说，一个motif就是一个3颗卫星、2条ISL连接的模式，在整个星座中重复。我们用motif来表示连接模式以及此模式的结果拓扑

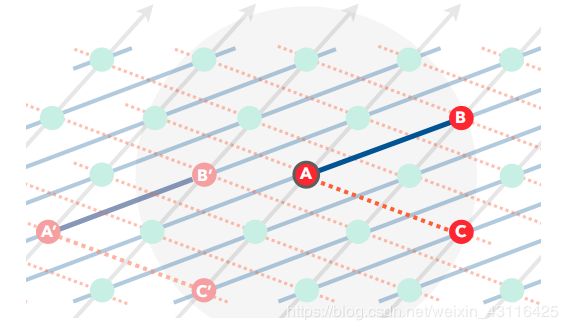
不同motif描述一个拓扑家族，这个家族包括网格。我们方法的最简单的版本就是穷举所有可能motif并选择性能最好的。对任意卫星，穷举包括找到该卫星附近符合所有距离限制的可直接点对点相连的所有卫星。值得注意的是，这个列表在赤道和在高纬度地区相去甚远，赤道处最少。因此，使用赤道处的枚举来保证这个列表对其他所有卫星都是可行的

找到卫星可达的所有卫星的集合后，枚举可行motif就可以直接从可达集中抽取两个。由于对称性，一些可行motif是等价的。基于此对称性，又能将motif的数量降低。

基于所有枚举的motif，可以简单的用任意流量矩阵进行评估，Φα值最小的将会被选中。

• 过程概述：
  选择赤道上一颗卫星e
  Se是e可达范围内所有卫星
  将从Se中抽取两个的所有组合组成motif集M
  将M中的等价motif剔除
  计算M中所有motif的Φα，值最小的就是最好的

4.2 无连接更换扰动

motif只覆盖了少量可能拓扑，但描述了所有稳定连接集，也就是，不会产生连接变化。如上面的例子中，A-B和A-C同步运动，因此他们在赤道的相对运动较小，只会在高轨变得稍大。这种变化与网格的特点一样是精准的。因此，卫星能够持续的连接到相同的卫星上，即使在高轨改变方向也能保持同样的连接。所以说motif提供了一个长期、稳定的连接

4.3 在任意一个快照中的性能

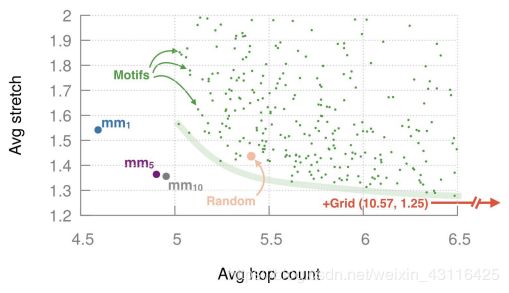
在与前面提到的相同的$40^2$卫星星座中，我们找到了1029个motif，对这些motif，下图给出了它们在某个随机快照中的拉伸及跳数分布。为清晰起见，修建了一些过度拉伸和过度多跳数的motif，同时在图中加入了随机图，该随机图是进行了100此尝试获得的平均值，其中网格的拉伸和跳数均值为1.25和10.57。透过结果可以发现：

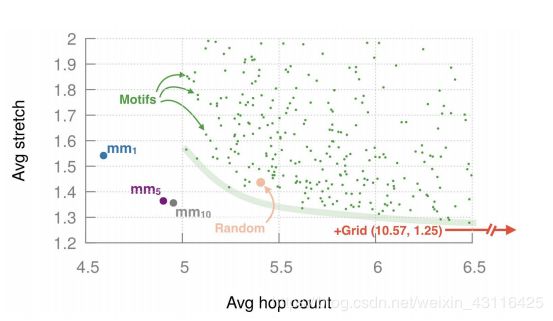
1. 不同motif的表现会非常不同
2. motif在拉伸和跳数之间进行均衡，一些motif到达了帕累托边界。随机图只在设计空间中提供了一个点
3. 在帕累托边界上的点的变现超过了随机图，这能允许我们优化更加看重的属性
4. 网格几乎有最低的拉伸，但跳数过多。有的motif相对于网格牺牲2%(10%)的拉伸量，可获得跳数32%(47%)的提升

系统范围的平均值外，也进行了城市对的分别对比。最好的motif相对于网格对M1，M5和M10的提升中值(95%值)分别是44.5%(54%)、26.2%(37%)和16.8%(22.3%)
可惜的是我们无法运行线性规划的结果作为对比。对可支持的最大规模的线性规划，它相对于网格的Φ1优化54%。Φ1motif相对于网格优化45%，比线性规划差18%。但由于线性规划太复杂不可使用

4.4 随时间变化的性能

虽卫星网络相对于地面运动，motif是否能应对这种变化的流量？使用与上面相同的Φ1中最优motif运行了2小时，每隔1分钟进行更新，这个时长已经超过了轨道周期

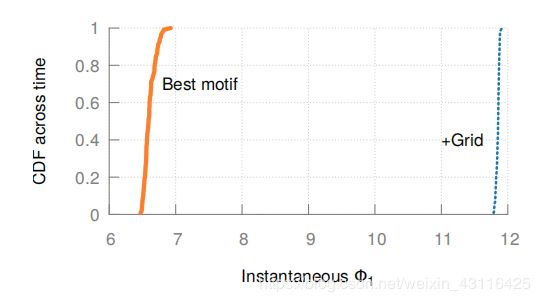
如图可以看到，最优motif的中值比网格中值优44%（对95%值优化43%）。Φ1随时间变化量在10%以内。因此，motif能提供更优的结果，而不进行任何的动态配置。

这个描述太秀了！很多设计都是牺牲了原有的静态性来提升整体的吞吐，可是这里纯粹的进行了一个静态拓扑的设计然后就能不增加任何动态改变的提升网络能力，完全不是trade off，是improvement啊！

4.5 星座配置的影响

• 星座大小：
  对统一配置（53°，550km）的星座设定不同大小：$16^2，24^2，32^2，40^2$。对小型星座，网格和最优motif都会让许多城市对没有连接，且没有连接的城市对数相同，这是由于这些都源自于地站的可见性而非ISL设定。所以我们的仿真都只针对于可连接的城市对。
  
  如图可见，随着规模扩张，motif方法将会有更好的收益。这与随着密度增加，可选motif数量增加有关。网格随着规模增加收益降低看起来比较奇怪，这是因为尽管拉伸减少，但跳数剧增。
  结果也表现了星座从以前那种更小型星座转向未来预计中更大型的星座时，性质的改变。对小型星座，更多的时寻找最低的高度来尽可能清除中间层
• 倾角：
  设定了550km的$40^2$的对照试验来对比。极地轨道的中数提升是46%，53°倾角的提升则为44.5%。53°倾角轨道相较于极地有14%的降低，因为倾斜轨道在人口稠密区花费时间较长，更适合我们的模型
  

4.6 加入功率限制

上面的实验中仅考虑了可见性，只要在5014km内的ISL都视为可连的。但我们需要加入功率考虑。

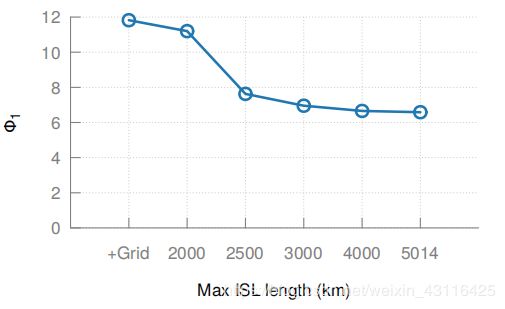
对$40^2$的卫星星座，最长的网格连接时1467km，在这个长度与5014km之间作为motif允许的最长长度进行计算，发现在允许最长长度是3000km的时候就已经接近于允许可见连接的最优了。因为卫星设计的最初目的是网络连接，所以可以预见它们的设计不会严格限定在1467km而是会更长，而且前面也讨论过，现在的技术已经可以实现非常长的通信范围。实际上，像Telesat这样的卫星会需要更高的连接距离（6000km）。而且，在操作上也会因为需要分布发射部署，所以需要更长的ISL范围。

4.7 不同的流量矩阵

网格拓扑是完全与流量无关的，motif则在某种程度上受流量影响，对motif的选择有非常大的空间。当然，这个选择空间相对于整数规划非常有限。
流量最终将取决于市场、监管以及地理变化，我们很难仿真正确的流量矩阵。因此，我们选择了一种基于人口的矩阵生成方式。这里我们提出另一种直觉上的流量矩阵，即基于经济行为的方式。
我们将GDP代替流量进行计算，选用100个已知城市GDP，城市间的流量按照城市对的GDP乘积大小映射到[0,1]区间内。对一个$40^2$的倾斜星座，最好的motif比网格好34%，虽然比使用人口的要差，但也是一个大的提升。
考虑到随时间变化的流量，我们可以模拟一个快照的流量选定最佳的motif，然后隔一段时间进行改变。

问题：相对于不同的流量矩阵选用的motif不同，那地面不同时间的流量差距很大该怎么办？实际的提升根本不会达到预期这么大，甚至基本没什么提升，因为流量矩阵是变化的，而motif选择是根据流量决定的， 因此根据某个流量选定的motif可能在其他时候的提升没那么大。使用快照，那你原来说的那个不用改变的优势全都没了！！！

5 更丰富的使用motif

简单使用一个motif就已经能相对于网格有一个很大的提升了，接下来，如果我们允许一个小型的可配置、可控制，就能有一个更高的提升。

5.1 不均匀的卫星距离

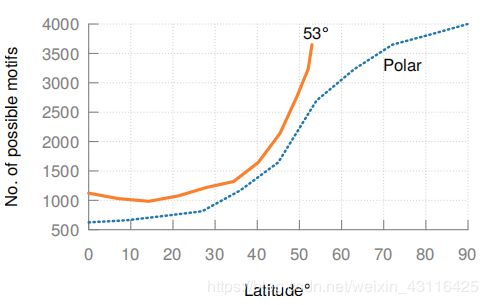
无论极地还是非极地轨道，卫星密度都是不均匀的，因此在高纬度，对于一个固定的最大ISL范围，卫星可建立ISL的范围会更大。如图是对不同纬度的可选motif的数量（可建ISL距离设定为5014km）。可以看到可建立ISL随着纬度增高逐渐增加。对53°倾斜轨道，在赤道可选motif约1100个，到53°则达到约3600个。而且这种密度变化不仅仅是临时出现在一个快照中的，而是一个持久的特性。如果仅仅使用一种motif而忽略了这种随纬度变化的特性并非一个好的办法

5.2 穷尽的多motif搜索？

在前面我们通过穷尽尝试所有motif搜索到了最适用的motif，这让我们考虑是否能使用同样的方案来寻找最好的面向不同纬度的motif组合

逻辑上可以把卫星轨道分进四个象限，利用对称性，仅在一个象限内穷尽搜索。对$40^2$的星座，一个象限中至少有10个卫星。从上图中可以看出，每个卫星都有$10^3$数量级的motif可选项，那么对于十个卫星，就有$10^{30}$个多motif组合。评价一个组合需要计算大规模城市对之间的最短路径以及跳数，需要在networkx 中计算数十秒，即使并行计算，这个计算也未免过于复杂，百万核的计算机大约计算$10^{20}$天。所以这样的穷举是不可取的，需要进行优化

5.3 一个粗糙、迭代的搜索

为克服穷举的复杂性，我们使用迭代启发式方案。我们考虑W为一个域囊括W°的纬度。对53°的星座，若W=18，那就分为三个域0-18，18-36，36-53。

将每个域分别考虑。从纬度最低的域开始。在一个域内，纬度最低的决定可行的motif（因为那里卫星间距最大），然后将这个motif填充整个星座并计算Φ1获得最佳。

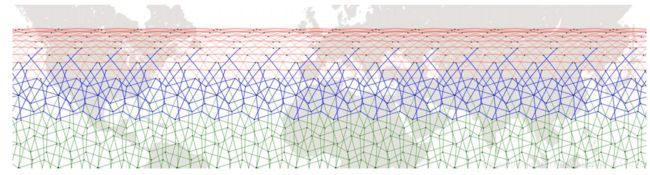
到下一个域时，除掉除了已经定下来的区域的所有ISL，然后对所有没有填充motif的域再来一次motif的选择，直到所有的域都被填充好。下图是进行迭代填充后三个域选的motif，设定W=18°，最大ISL长度是2000km

5.4 性能和链路变化

不同于单种motif的拓扑设计，多域设计中卫星需要跨域的时候ISL需要进行改变。上面的卫星ISL每12min改变一次，这对于几秒到几十秒的改变耗费是可行的。更小的W可能对一个静态的快照性能有所改善但会增加链路变化。而且我们发现在三个分区以后性能的提升将会饱和。对3或多个分区，相较于单motif的提升是7%；2个分区的提升是5.6%。对$40^2$的极地轨道，18°多分区将会比单motif提升9.5%。多motif还相对于单motif降低了多变性，如下图所示

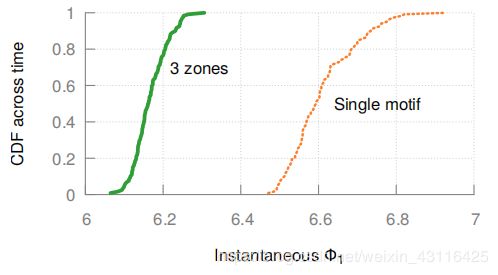
对不同度量的性能

不同的度量对拉伸（S）和跳数（B）的比例要求不同，因此我们还评估了我们的方案在Mα=Sα+B时，对M1，M5及M10的提升。
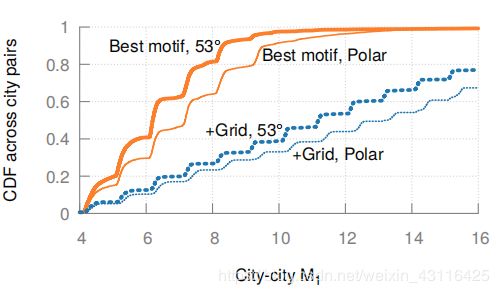
下图除了单motif还加入了3motif的评测结果，它们都优于帕累托边界。相对于网格的Φ1，Φ5和Φ10的优化分别是48%，30%和20%。

• 基础度量：
  在前面的讨论中为简单起见粗暴的将S和B加起来并未S赋α权值。但实际上这个α没有任何含义。而且过高的α会使得实际的改进被低估。因为拉伸相对于跳数在拓扑设计中并没有那么高的地位。比如，对Φ10的相对于网格的20%的提升中，包括了跳数的53%的提升以及9%的拉伸的增加。而前面提到，即使少量的拉伸的牺牲能换取很大的跳数的减少。

//这里作者比较诡辩。不同于地面网络，卫星网络主要的延迟在传播时延上，所以拉伸很重要。尽管前面提到的跳数与拥塞有一定的关系，但只是直观上的。没有将实际上拥塞的改进进行一个量化达到说服读者的目的是本文的一个缺憾，因为如果能有相关的验证来证明跳数降低能减少拥塞，这个地方的说法就不会那么生硬

牛逼！我刚在上面说到这厮缺憾，下一节立马出来评估！让我来看看这厮如何证明的！

5.6 跳数和拥塞

跳数直觉上与网络容量有关。端点之间跳数越少，也就意味着一个连接会占用的整体容量就越少。我们使用最短路径路由算法来进行跳数与拥塞之间的关系的分析

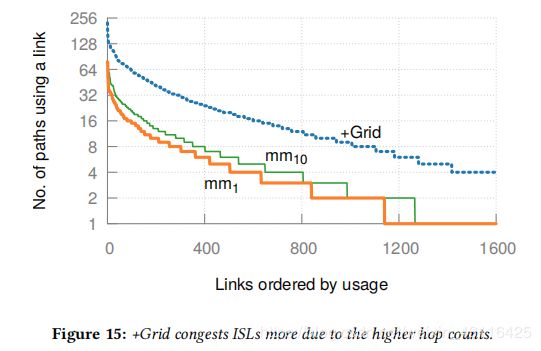
对上述3motif实例，使用最低时延路由算法。对任意选择的5000个城市对，计算最低时延路径并记录每一个ISL在路径中出现的频率。下图将所有被用过的ISL按照使用频率进行排序得到分布。相较于多motif方案，网格选择的很多ISL都4倍甚至5倍的频繁使用超过mm1。而对于多motif方案，拉伸权重更高的mm10的拥塞程度超过了mm1，可证5.5的说法。

作者牛皮！

6 优化starlink和kuiper

我们的方案是一个足够概化的方案，能优化任意星座，我们通过Starlink和Kuiper来验证它的有效性

• SpaceX Starlink
  使用最大ISL范围5014km和最小ISL范围2006km作为最好和最差情况下的限制条件进行24轨道共1584颗卫星（53°，550km）的优化。
• Amazon Kuiper：
  它最初的方案是34^2（51.9°，630km）星座，最优和最差条件分别是5440km和1761km
• 结果：
  
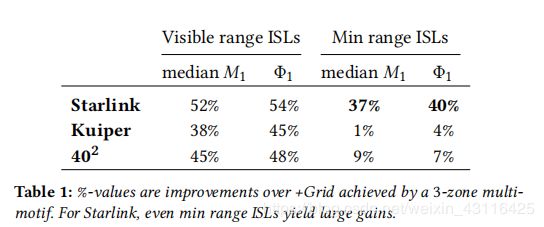
  Starlink即使最差也能提升37%，这是由于它的轨道比较少，使得轨道间距要求更高，所以可设计性提升

7 限制和未来工作

由于公司对一些技术的保密性，造成了一些挑战：

1. 卫星的ISL建立范围和时间受一系列复杂的非网络原因影响，比如卫星重量、发射成本，因此在拓扑设计时不能近似为0
2. 市场条件、监督监管以及地面连接会影响卫星网络的负载，因此流量矩阵无法进行实际的模拟
3. 国际空间管理经常会改变，所以我们研究的条件是一直变化的。比如，在我们研究过程中，SpaceX更新了对Starlink的设定，所以我们只用了到2019年6月的数据

但这些不确定性并不会成为我们无法攻克难关的原因。因此，我们试图通过考虑一组广泛的可能的输入来解决不确定性，例如，ISL的最佳情况到最差情况范围，较慢或较快的链接设置，以及两个直观的流量模型。即使最保守假设我们的工作也表现出了很好的提升。

我们后续工作将会在这些方面开展：考虑流量变化，考虑大型星座之间与地面的连接，联合设计卫星轨道和路由等。

8 相关工作

在HotNets 2018 workshop中，三个意见书出现在研讨会上。两份关注路由，一份描绘了LEO网络的承诺和挑战，其中就列出了拓扑设计问题，但并没有确切的框架，其重点是轨道设计，没有提到ISL互联。最近的一篇文章介绍了Starlink、Telesat和OneWeb，讨论地站数量如何影响整体。这个分析使用了网格的连接。这篇文章可以当作我们工作的一个例子：作者展示了如果ISL连接容量随技术进步而增加，这将大大推动系统吞吐。同样的收益可以通过有效的的使用ISL（我们提出的方案这样）被实现。另一项研究解决了一对小的、资源有限的立方体卫星之间的连通性。这是一个不同的问题，只解决成对的立方体卫星-立方体卫星的连接，而不是通过卫星的互联网连接。

在90年代有一股卫星网络热潮，产生了大量学术工作，这些之中我们只讨论最相关的。Wood讨论了轨道设计和网格连接，这是我们对比的对象。Gavish和 Kalvenes讨论四种手工设计极地轨道的Π卫星设计变种，这里存在一个缝的问题。相反，在现在星座中我们普遍使用2Π设计解决了缝的问题。另外，新星座的设计密度展现了很多的设计选择。像我们所提出的，随着密度增加整个问题的特性都改变了，可选择的连接将会爆发，手动设计变得不现实。

有些工作也会影响或被ISL拓扑设计所影响：轨道优化、路由设计。虽然相互依存，这些问题的复杂性似乎需要分解和单独处理，至少在这一领域的研究成熟的时候是这样

动态链接在其他领域被研究，包括高铁、无人机、飞机。但它们中没有同时考虑我们问题的特性：移动可预测、大规模、高速、相互多连接、为固定端点提供连接。这个问题从根本上与以前的工作不同，并且需要不同的解决方案

在图论上，motif和graphlets都已经被很好的研究了，但本文从一个不同的角度，识别一个给定图中重复连接模式模式。当然，即使在设计的角度，重复模式的使用也已经被长期使用，比如，在视觉和图形设计。据我们所知，我们是第一个系统的将这个想法放入卫星设计的。

9 结论

我们为大型卫星星座进行了网络设计，网络需要在一部分星间连接的情况下为大型流量提供低时延的交流。这个问题表面上像是个已经被研究过的网络设计问题。但是，我们从这些问题的经验中对直觉方法的系统分析暴露了它们在这方面的局限性，并希望将推动这一领域的未来工作向新的、专门的技术发展。我们使用重复模式来消解系统的时间动态问题，实现了比最新技术2倍的提升。我们还发现如果将问题在几何上进行分解，允许小部分的控制和动态链路变化，将会获得更优的结果。对目前最成熟的最大的系统Starlink，我们的方法能保证54%性能的提升，即使在最差的情况也能有40%的提升。通过分析一个不确定的限制，我们努力达到一个鲁棒的结果，希望我们的设计能改变以后正在计划中的卫星星座，并激励后续在相关方向的研究

个人评价

1. 这种拓扑的设定是根据固定的流量设计的，所以对不同的流量，最优motif可能相差很大。表面上这种设计变化性低，实际上，每天不同时间段的流量变化很大，选定什么流量进行motif设计？平均流量吗？
2. 不同区域的需求量差距也比较大，但这个设计本质还是一个均匀拓扑。

附

本文相关引用、数据：

（1） 相关可用引用：

1. HughesNet. 2018. HughesNet: America’s #1 Choice for Satellite Internet. https://www.hughesnet.com/. (2018). 使用数十颗GEO为农村地区提供有限的几千万的接入
2. Inigo del Portillo, Bruce G Cameron, and Edward F Crawley. 2019. A technical comparison of three low earth orbit satellite constellation systems to provide global broadband. Acta Astronautica (2019). 通过提升星间链路的容量颗有效提升整体吞吐
3. David S Johnson, Jan Karel Lenstra, and AHG Rinnooy Kan. 1978. The complexityof the network design problem. Networks 8, 4 (1978), 279–285. 网络设计问题的复杂性
4. SatNet authors. 2019. Polar and inclined orbits with +Grid connectivity. https://satnet-authors.github.io/cesium_orbit_grid_demo.html. (2019). 极地卫星和倾斜卫星
5. Debopam Bhattacherjee and Ankit Singla. 2019. Network topology design at 27,000 km/hour. https://satnetwork.github.io. (2019). 本文的核心数据和代码
6. marine.rutgers.edu. 2001. Keplerian Elements. https://marine.rutgers.edu/cool/education/class/paul/orbits.html. (2001). 完全描述轨道需要7个参数
7. Zoran Sodnik, Bernhard Furch, and Hanspeter Lutz. 2010. Optical intersatellite communication. IEEE journal of selected topics in quantum electronics 16, 5 (2010),1051–1057. 星间激光链路通信能达到4900km5.6Gbps的程度
8. ESA. 2013. Alphasat Optical Communication. https://tinyurl.com/y23vthrs. (2013). GEO和LEO高速通信
9. Mark Handley. 2018. Delay is Not an Option: Low Latency Routing in Space. In ACM HotNets. 推测ISL容量可达到数十Gbps
10. Berry Smutny, Hartmut Kaempfner, Gerd Muehlnikel, Uwe Sterr, Bernhard Wandernoth, Frank Heine, Ulrich Hildebrand, Daniel Dallmann, Martin Reinhardt, Axel Freier, et al. 2009. 5.6 Gbps optical intersatellite communication link. In Free-Space Laser Communication Technologies XXI, Vol. 7199. International Society for Optics and Photonics, 719906. ISL的建立时间在s到数十秒间取决于建立的技术和相对速度
11. Lloyd Wood. 2001. Internetworking with satellite constellations. Ph.D. Dissertation.University of Surrey. 网状设计的科学性和工程可行性
12. Ankit Singla, Chi-Yao Hong, Lucian Popa, and P Brighten Godfrey. 2012. Jellyfish:Networking data centers randomly. In USENIX NSDI. 数据中心网络中使用随机图
13. Oliver Montenbruck and Eberhard Gill. 2012. Satellite orbits: models, methods and applications. Springer Science & Business Media. 对卫星轨道的总结，可看！
14. Debopam Bhattacherjee, Waqar Aqeel, Ilker Nadi Bozkurt, Anthony Aguirre, Balakrishnan Chandrasekaran, P Godfrey, Gregory Laughlin, Bruce Maggs, and Ankit Singla. 2018. Gearing up for the 21st century space race. In ACM HotNets. LEO网络设计的挑战
15. Mark Handley. 2018. Delay is Not an Option: Low Latency Routing in Space. In ACM HotNets. LEO星座路由设计，下同
16. Tobias Klenze, Giacomo Giuliari, Christos Pappas, Adrian Perrig, and David Basin. 2018. Networking in Heaven as on Earth. In ACM HotNets.
17. Inigo del Portillo, Bruce G Cameron, and Edward F Crawley. 2019. A technical comparison of three low earth orbit satellite constellation systems to provideglobal broadband. Acta Astronautica (2019). 对Starlink，TeleSat和OneWeb的介绍
18. Lloyd Wood. 2001. Internetworking with satellite constellations. Ph.D. Dissertation. University of Surrey. 轨道设计和网格连接
19. Bezalel Gavish and Joakim Kalvenes. 1997. The impact of intersatellite communication links on LEOS performance. Telecommunication Systems 8, 2-4 (1997), 159–190. 四种手动设计的Π星座

（2）数据：

1. WonderNetwork. 2019. Global Ping Statistics. https://wondernetwork.com/pings. (2019). 模拟世界范围内两点之间通信的时延
2. NetworkX developers. 2019. NetworkX. https://networkx.github.io/. (2019). 在2002年5月产生，是一个用Python语言开发的图论与复杂网络建模工具，内置了常用的图与复杂网络分析算法，可以方便的进行复杂网络数据分析、仿真建模等工作。
3. Greater London Authority (GLA). 2018. Global City Population Estimates. https://data.london.gov.uk/dataset/global-city-population-estimates. (2018). 人口预测
4. Wikipedia. 2014. “2014 est. PPP-adjusted GDP ($BN)” by Brookings Institution.https://en.wikipedia.org/wiki/List_of_cities_by_GDP. (2014). 城市GDP数据

（3）卫星星座：

1. Starlink：
   ①SpaceX Starlink. 2017. https://www.spacex.com/webcast. (2017).
   ②SpaceX FCC filing. 2017. SpaceX V-BAND NON-GEOSTATIONARY SATELLITE SYSTEM. https://tinyurl.com/kkskns4. (2017).
   ③SpaceX FCC update. 2018. SPACEX NON-GEOSTATIONARY SATELLITE SYSTEM. https://licensing.fcc.gov/myibfs/download.do?attachment_key=1569860. (2018).
2. Kuiper：
   ①Alan Boyle. 2019. Amazon to offer broadband access from orbit with 3,236-satellite ‘Project Kuiper’ constellation. https://www.geekwire.com/2019/amazon-project-kuiper-broadband-satellite/. (2019).
   ②Kuiper USASAT-NGSO-8A ITU filing. 2018. https://www.itu.int/ITU-R/space/asreceived/Publication/DisplayPublication/8716. (2018).
   ③ Kuiper USASAT-NGSO-8B ITU filing. 2018. https://www.itu.int/ITU-R/space/asreceived/Publication/DisplayPublication/8774. (2018).
   ④Kuiper USASAT-NGSO-8C ITU filing. 2018. https://www.itu.int/ITU-R/space/asreceived/Publication/DisplayPublication/8718. (2018).
3. OneWeb：OneWeb. 2018. How OneWeb is changing global communications. http://www.oneweb.world/. (2018).
4. Telesat：
   ①Telesat. 2018. Telesat’s responses - Federal Communications Commission. http://licensing.fcc.gov/myibfs/download.do?attachment_key=1205775. (2018).
   ②Telesat. 2019. Satellite Services for Broadcast-Telecom-Corporate-Government-Satellite Services in North America-South America-Asia-Europe-Ka. https://www.telesat.com/. (2019).
5. LeoSat：LeoSat. 2018. A New Satellite Paradigm and Unique Data Network Solution.http://leosat.com/. (2018).
6. Hongyan：Andrew Jones. 2018. China to launch first Hongyan LEO communications constellation satellite soon. https://tinyurl.com/y4anchw7. (2018).
7. Iridium：Iridium Communications Inc. 2018. Iridium Satellite Communications. https://www.iridium.com/. (2018).