FFT快速傅里叶变换(HDU1402)
第一次写博客,可能很烂,多多指教
快速傅里叶变换FFT及HDU1402编程实现
说起快速傅里叶变换,首先要了解一下什么是傅里叶变换。对于傅里叶变换,简单来说就是任何连续周期信号可以由一组适当的正弦曲线组合而成,例如:
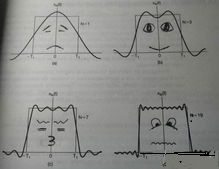
(图片来源:百度百科)
第一幅图是一个余弦波 cos(x)
第二幅图是 2 个余弦波的叠加 cos (x) +a.cos (3x)
第三幅图是 4 个余弦波的叠加
第四幅图是 10 个余弦波的叠加
由于数学能力不强,就不再进行更深入的解释,我是通过观看傅里叶变换形象展示来对此概念进行初步了解的。根据视频里面所述,傅里叶变换表示为
g ^ ( f ) = ∫ ∞ ∞ g ( t ) e − 2 π i f t d t . \hat{g}(f) = \int_\infty^\infty {g}(t)e^{-2\pi ift}dt\,. g^(f)=∫∞∞g(t)e−2πiftdt.
由于 f = 1 / T f = 1/T f=1/T, w = 2 π / T w = 2\pi /T w=2π/T,则
g ^ ( f ) = ∫ ∞ ∞ g ( t ) e − i w t d t . \hat{g}(f) = \int_\infty^\infty {g}(t)e^{-iwt}dt\,. g^(f)=∫∞∞g(t)e−iwtdt.
FFT为离散傅里叶变换 DFT 的一种快速算法。上式中计算出来的是信号的连续频谱,在实际中用连续信号的离散采样值来计算信号的频谱。则对于N点有限长序列x(n)的DFT 为
X ( k ) = ∑ n = 0 N − 1 x ( n ) W N n k , W N n k = e − i n k 2 π / N {X}(k) = \displaystyle\sum_{n=0}^{N-1}{x}(n)W_{N}^{nk }, W_{N}^{nk} = e^{-ink 2\pi /N} X(k)=n=0∑N−1x(n)WNnk,WNnk=e−ink2π/N
其逆变换IDFT为
x ( n ) = 1 / N ∑ n = 0 N − 1 X ( k ) W N − n k , W N − n k = e i n k 2 π / N {x}(n) = 1/N\displaystyle\sum_{n=0}^{N-1}{X}(k)W_{N}^{-nk }, W_{N}^{-nk} = e^{ink 2\pi /N} x(n)=1/Nn=0∑N−1X(k)WN−nk,WN−nk=eink2π/N
对此,我们发现DFT和IDFT中没计算一次X(k),需要N次乘法和N-1次加法,X(k)有N个点,因此运算量为N * N次乘法和N * (N-1)次加法,因此复杂度为O(n^2)。
运用FFT可使复杂度从O(n^2)变为 O(NlogN),基本原理就是通过分治把长的DFT分解为多个短的DFT,最终将N点DFT分解为N/2个两点DFT,然后通过 W N n k W_{N}^{nk} WNnk的周期性和对称性来减少运算次数。
下面直接做题HDU1402(使用kuangbin模板)
import java.util.Scanner;
public class Main{
static final double PI = Math.acos(-1.0);
static complex[] x1;
static complex[] x2;
static int[] sum;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while(in.hasNext()) {
String str1 = in.next();
String str2 = in.next();
int len1 = str1.length();
int len2 = str2.length();
int len = 1;
while(len < len1*2 || len < len2*2) len <<= 1;
x1 = new complex[len];
x2 = new complex[len];
sum = new int[len+1];
for(int i = 0;i < len1;i++)
x1[i] = new complex(str1.charAt(len1-1-i)-'0',0);
for(int i = len1;i < len;i++)
x1[i] = new complex(0,0);
for(int i = 0;i < len2;i++)
x2[i] = new complex(str2.charAt(len2-1-i)-'0',0);
for(int i = len2;i < len;i++)
x2[i] = new complex(0,0);
fft(x1,len,1);
fft(x2,len,1);
for(int i = 0;i < len;i++)
x1[i] = x1[i].mul(x2[i]);
fft(x1,len,-1);
for(int i = 0;i < len;i++)
sum[i] = (int)(x1[i].r+0.5);
for(int i = 0;i < len;i++)
{
sum[i+1] += sum[i]/10;
sum[i] %= 10;
}
len = len1+len2-1;
while(sum[len] <= 0 && len > 0)len--;
for(int i = len;i >= 0;i--) {
System.out.print(sum[i]);
}
System.out.println();
}
}
public static void change(complex y[],int len) {
int i,j,k;
for(i = 1, j = len/2;i < len-1; i++)
{
if(i < j)y[i].swap(y[j]);
k = len/2;
while(j >= k)
{
j -= k;
k /= 2;
}
if(j < k) j += k;
}
}
public static void fft(complex y[],int len,int on)
{
change(y,len);
for(int h = 2; h <= len; h <<= 1)
{
complex wn = new complex(Math.cos(-on*2*PI/h),Math.sin(-on*2*PI/h));
for(int j = 0;j < len;j+=h)
{
complex w = new complex(1,0);
for(int k = j;k < j+h/2;k++)
{
complex u = y[k];
complex t = w.mul(y[k+h/2]);
y[k] = u.add(t);
y[k+h/2] = u.sub(t);
w = w.mul(wn);
}
}
}
if(on == -1)
for(int i = 0;i < len;i++)
y[i].r /= len;
}
}
class complex{
double r,i;
public complex(double _r,double _i){
r = _r;
i = _i;
}
public complex add(complex b) {
return new complex(r+b.r,i+b.i);
}
public complex sub(complex b) {
return new complex(r-b.r,i-b.i);
}
public complex mul(complex b) {
return new complex(r*b.r-i*b.i,r*b.i+i*b.r);
}
public void swap(complex b) {
double t1 = r;
double t2 = i;
r = b.r;
i = b.i;
b.r = t1;
b.i = t2;
}
}
于此同时,该题可直接使用Java的大数乘法求解
import java.math.BigInteger;
import java.util.Scanner;
public class Main{
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while(in.hasNextBigInteger()) {
BigInteger x = in.nextBigInteger();
BigInteger y = in.nextBigInteger();
System.out.println(x.multiply(y));
}
}
}
关于傅里叶变换以及FFT的一些细节还没有很好掌握,需要进一步学习和练习