利用线性筛算法框架求解因数个数以及因数和问题
利用线性筛算法框架求解因数个数以及因数和问题
一 前言
关于线性筛算法,在前一篇文章 利用线性筛以及素数筛求某一范围内的所有素数中已经介绍过,若读者对线性筛算法不太了解或有所遗忘,可以点击链接查看。此处我们将直接利用线性筛算法的框架,求解某个数字所有因数的个数,以及所有因数的和。
二 问题阐述
As we all know, 任意数字都可以写成其因数乘积的形式,我们要做的就是找出该数字对应因数的个数以及所有因数的和,详细问题描述如下:
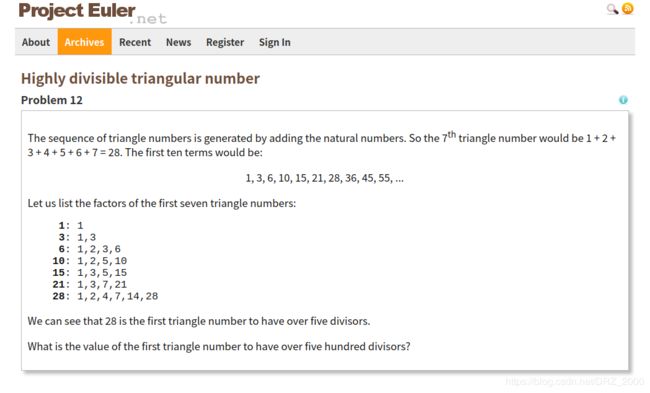
欧拉计划12题——求解第一个因数个数超过500的三角形数字
 欧拉计划21题——求所有小于10000的亲和数的和
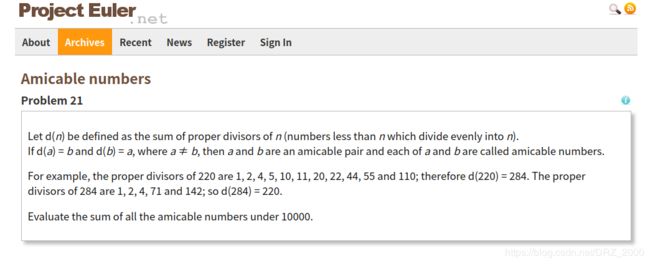
欧拉计划21题——求所有小于10000的亲和数的和
三 问题分析
- 对于第一个问题,首先弄明白什么是三角形数字?
1, 3, 6, 10, 15…
观察序列可知,其对应的表达式为:n(n + 1) / 2,即三角形数字的生成公式为:n(n + 1) / 2
所以现在我们要做的就是判断当前数字因数的个数,怎么判断? 暴力枚举吗?还是别的? - 对于第二个问题,我们先再捋一遍题意
令d(n)表示数字的所有真因数的和(所谓真因数就是 除自己以外的其他所有因数)
若d(m) = n 并且 d(n) = m,那么我们称n, m是一组亲和数
例如:d(220) = 1 + 2 + 4 + 5 +10 + 11+ 20 + 22 + 44 + 55 + 110 = 284,并且 d(284) = 220,那么我们称220和284两个都是亲和数,现在我们要做的就是找出所有小于10000的亲和数,计算他们的和。 - 不难看出,上面两道题都涉及到因数这个概念,只不过第一题问的是因数的个数,第二题与因数的和有关。
四 解题思路及关键代码展示
我们将数字(此处仅指正整数)划分为两类:质数与合数。
若数字d为质数,那我们可以把它写成d = 1 * d 的形式,它所具有的因数也只有 1 和 d 本身;
若数字 d 是合数,更可以写成若干数相乘的形式,我们以24为例,24的因数有:1, 2, 3, 4, 6, 8, 12, 24 共 8 个,所以可以写成: 24 = 1 ∗ 24 24=1*24 24=1∗24, 24 = 2 ∗ 12 24=2*12 24=2∗12, 24 = 3 ∗ 8 24=3*8 24=3∗8, 24 = 4 ∗ 6 24=4*6 24=4∗6的形式,但这又如何?细心观察不难发现24的因数中有些因数可以写成其他因数的幂次的形式,例如 8 = 2 3 8 = 2 ^ 3 8=23,因此我们可以换一种写法: 24 = 2 3 ∗ 3 1 24 = 2 ^ 3 * 3 ^ 1 24=23∗31, 其实这是一个定理,我们可以将其一般化。
任何一个整数,都可以转换为其质因数幂次乘积的形式
n = p 1 a 1 ∗ p 2 a 2 ∗ p 3 a 3 ∗ . . . ∗ p n a n n = {p_1} ^ {a_1} * {p_2} ^ {a_2} * {p_3} ^ {a_3} * ... * {p_n} ^ {a_n} n=p1a1∗p2a2∗p3a3∗...∗pnan , 其中 p i p_i pi表示数字n的质因数, a i a_i ai表示对应的幂次
这时小编可以很快的得出24拥有因数的个数为8, 为何??
现在我们定义两个集合 A = { 2 0 2 ^ 0 20, 2 1 2 ^ 1 21, 2 2 2 ^ 2 22, 2 3 2 ^ 3 23},B = { 3 0 3 ^ 0 30, 3 1 3 ^ 1 31} , 我们从集合A和集合B中各选一个数,将它们相乘,乘得的结果就是24的因数,并且不会出现重复。因此因数个数为: C 4 1 ∗ C 2 1 C_4^1 * C_2^1 C41∗C21, 将结果一般化,若 n = ∏ i = 1 n p i a i n = \prod_{i = 1}^{n} {p_i} ^ {a_i} n=i=1∏npiai则数字n因数的个数为: C a 1 + 1 1 ∗ C a 2 + 1 1 ∗ . . . ∗ C a n + 1 1 C_{a_1 + 1}^1 * C_{a_2 + 1}^1 * ... * C_{a_n + 1}^1 Ca1+11∗Ca2+11∗...∗Can+11
此时第一题的关键就在于找到数字n的质因数以及质因数对应的幂次!!!,为便于描述,我们将结合代码进行阐述。
之前采用线性筛挑选素数的关键代码如下:
#define max_n 1000000
int prime[max_n + 5] = {0};
void init() {
for (int i = 2; i <= max_n; i++) {
if (!prime[i]) prime[++prime[0]] = i;
for (int j = 1; j <= prime[0]; j++) {
if (i * prime[j] > max_n) break;
prime[i * prime[j]] = 1;
if (i % prime[j] == 0) break;
}
}
}
代码解释:
-
首先从2开始到max_n进行遍历
-
若当前prime[i] == 0,也就是 i 为素数,此时我们为便于操作,从prime数组的1号位开始向后依次存放找到的素数。
-
若当前prime[i] != 0,即数字 i 为合数,此时我们利用数字 i 将某些数字标记为合数 (标记为1),应该是哪些数字??? 我们利用已经找到的素数 (之前不是从prime数组1号位置开始向后存储了吗!),若该素数 (假设为prime[j] ) 比数字 i 的最小素因子还要小,那我们可以标记prime[i * prime[j]] = 1; 因为prime数组中从 1 号位向后的素数是逐渐增大的,因此一定会到某一个素数prime[j],此时prime[j]不小于数字 i 的最小质因数,也就不满足我们线性筛的基本要求,此时break跳出。
第一题关键代码展示如下:
#define max_n 100000000
int prime[max_n + 5] = {0}; //素数表,存储找到的素数
int f[max_n + 5] = {0}; //f[i]表示数字i的因数的个数
int cnt[max_n + 5] = {0}; //cnt[i]表示数字i 最小质因数的幂次
void init() {
for (int i = 2; i <= max_n; i++) {
if (!prime[i]) { //若数字i是素数
prime[++prime[0]] = i; //存放在prime数组中
f[i] = 2; //素数的因数只有1和本身,所以f[i] = 2
cnt[i] = 1; //i = 1 * i,所以最小质因数的幂次为1
}
//遍历之前找到的素数,若prime[j] 小于数字i的最小质因数,则我们标记prime[i * prime[j]] = 1
for (int j = 1; j <= prime[0]; j++) {
if (i * prime[j] > max_n) break; //我们只要在2到max_n范围内的素数,若超过max_n,此时直接跳出
prime[i * prime[j]] = 1;
if (i % prime[j] == 0) {
//这部分解释见下文
f[i * prime[j]] = f[i] / (cnt[i] + 1) * (cnt[i] + 2);
cnt[i * prime[j]] = cnt[i] + 1;
break;
} else { //prime[j]是素数,因此i和prime[j]的因数最多是1和prime[j],又i % prime[j] != 0,所以i和prime[j]互素
f[i * prime[j]] = f[i] * f[prime[j]];
//两元素互素,因此他们的因数除1外没有交集,所以i * prime[j]的因数个数 = i的因数个数 * prime[j]的因数个数
cnt[i * prime[j]] = 1;
//因为从prime数组1号位开始向后遍历素数并且i % prime[j] != 0,所以prime[j]始终小于i的最小质因数,
//所以i * prime[j]最小质因数的幂次为prime[j]的幂次,即为1
}
}
}
return ;
}
代码解释:
- 这里我们只解释内层for循环中 if (i % prime[j] == 0) 的情况,剩余解释看代码注释
- 当i % prime[j] == 0 时,素数prime[j]恰为数字 i 的最小质因数,我们来看
若数字 i = p 1 a 1 ∗ p 2 a 2 ∗ p 3 a 3 ∗ . . . ∗ p n a n i = {p_1} ^ {a_1} * {p_2} ^ {a_2} * {p_3} ^ {a_3} * ... * {p_n} ^ {a_n} i=p1a1∗p2a2∗p3a3∗...∗pnan , 则 f [ i ] = C a 1 + 1 1 ∗ C a 2 + 1 1 ∗ . . . ∗ C a n + 1 1 f[i] = C_{a_1 + 1}^1 * C_{a_2 + 1}^1 * ... * C_{a_n + 1}^1 f[i]=Ca1+11∗Ca2+11∗...∗Can+11
此时数字 p 1 p_1 p1是 i 的最小质因数,那么prime[j] 就等于 p 1 p_1 p1
而 i ∗ p r i m e [ j ] i * prime[j] i∗prime[j]可以转换为: i ∗ p r i m e [ j ] = p 1 a 1 + 1 ∗ p 2 a 2 ∗ p 3 a 3 ∗ . . . ∗ p n a n i * prime[j] = {p_1} ^ {{a_1} + 1} * {p_2} ^ {a_2} * {p_3} ^ {a_3} * ... * {p_n} ^ {a_n} i∗prime[j]=p1a1+1∗p2a2∗p3a3∗...∗pnan
所以 f [ i ∗ p r i m e [ j ] ] = C a 1 + 2 1 ∗ C a 2 + 1 1 ∗ . . . ∗ C a n + 1 1 f[i * prime[j]] = C_{a_1 + 2}^1 * C_{a_2 + 1}^1 * ... * C_{a_n + 1}^1 f[i∗prime[j]]=Ca1+21∗Ca2+11∗...∗Can+11, 现在我们可以根据f[i]表示f[i * prime[j]]
即 f [ i ∗ p r i m e [ j ] ] = f[i *prime[j]] = f[i∗prime[j]]= f [ i ] / C a 1 + 1 1 f[i] / C_{a_1 + 1}^1 f[i]/Ca1+11 ∗ C a 1 + 2 1 * C_{a_1 + 2}^1 ∗Ca1+21
其中的 a 1 a_1 a1,就是最小质因数对应的幂次,这也是为什么我们在程序中引入cnt[max_n + 5]数组的原因,我们可以用cnt数组记录数字最小质因数对应的幂次
解释完第一题后我们再来看看第二题
第二题关键代码展示如下:
#define max_n 100000
int prime[max_n + 5] = {0}; //存储求得的素数
int f[max_n + 5] = {0, 1}; //f[i]表示数字i 所有因数的和
int cnt[max_n + 5] = {0}; //cnt[i]表示数字i 最小质因数的幂次
void init() {
for (int i = 2; i <= max_n; i++) {
if (!prime[i]) {
prime[++prime[0]] = i; //为质数,因此从prime数组1号位向后依次存储
f[i] = 1 + i; //因数只有i 和 1,所以f[i] = i + 1
cnt[i] = 1; //最小质因数为本身,所以cnt[i] = 1
}
for (int j = 1; j <= prime[0]; j++) {
//详细解释见下文
if (i * prime[j] > max_n) break;
prime[i * prime[j]] = 1;
if (i % prime[j] == 0) {
f[i * prime[j]] = f[i] / (pow(prime[j], cnt[i] + 1) - 1) * (pow(prime[j], cnt[i] + 2) - 1);
cnt[i * prime[j]] = cnt[i] + 1;
break;
} else {
f[i * prime[j]] = f[i] * f[prime[j]];
cnt[i * prime[j]] = 1;
}
}
}
return ;
}
代码解释:
与第一题类似,我们以24为例,其因数有:1, 2, 3, 4, 6, 8, 12, 24 共 8 个,并且根据定义两个集合 A = { 2 0 2 ^ 0 20, 2 1 2 ^ 1 21, 2 2 2 ^ 2 22, 2 3 2 ^ 3 23},B = { 3 0 3 ^ 0 30, 3 1 3 ^ 1 31} , 我们从集合A和集合B中各选一个数,将它们相乘,乘得的结果就是24的因数,并且不会出现重复(上文已说明)
那么 f [ 24 ] = f[24] = f[24]= 2 0 2 ^ 0 20 ∗ 3 0 *3 ^ 0 ∗30 + 2 0 2 ^ 0 20 ∗ 3 1 *3 ^ 1 ∗31 + 2 1 2 ^ 1 21 ∗ 3 0 *3 ^ 0 ∗30 + 2 1 2 ^ 1 21 ∗ 3 1 *3 ^ 1 ∗31 + 2 2 2 ^ 2 22 ∗ 3 0 *3 ^ 0 ∗30 + 2 2 2 ^ 2 22 ∗ 3 1 *3 ^ 1 ∗31 + 2 3 2 ^ 3 23 ∗ 3 0 *3 ^ 0 ∗30 + 2 3 2 ^ 3 23 ∗ 3 1 *3 ^ 1 ∗31,其中 f [ i ] f[i] f[i]表示 i 的因数和
整理之后不难发现: f [ i ] = ( 2 0 + 2 1 + 2 2 + 2 3 ) ∗ ( 3 0 + 3 1 ) f[i] = (2 ^ 0 + 2 ^ 1 + 2 ^ 2 + 2 ^ 3) * (3 ^ 0 + 3 ^ 1) f[i]=(20+21+22+23)∗(30+31), 细心观察我们可以看到每一项乘积不就是等比数列求和吗!!!
因此我们可以使用等比求和公式 S ( n ) = a 1 ∗ ( 1 − q n ) 1 − q S(n) = \frac{a_1 * (1 - q^n)}{1 - q} S(n)=1−qa1∗(1−qn), 此处 a 1 a_1 a1等于 1;q为公比;n为项数 ,所以我们化减 S ( n ) = p i a i + 1 − 1 p i − 1 S(n) = \frac{p_i^{a_i + 1} - 1}{p_i - 1} S(n)=pi−1piai+1−1, 即 f [ i ] = p i a i + 1 − 1 p i − 1 f[i] = \frac{p_i^{a_i + 1} - 1}{p_i - 1} f[i]=pi−1piai+1−1
现在我们将结果一般化:
若 n = p 1 a 1 ∗ p 2 a 2 ∗ p 3 a 3 ∗ . . . ∗ p n a n n = {p_1} ^ {a_1} * {p_2} ^ {a_2} * {p_3} ^ {a_3} * ... * {p_n} ^ {a_n} n=p1a1∗p2a2∗p3a3∗...∗pnan , 其中 p i p_i pi表示数字n的质因数, a i a_i ai表示对应的幂次
则: f [ n ] = f[n] = f[n]= p 1 a 1 + 1 − 1 p 1 − 1 \frac{p_1^{a_1 + 1} - 1}{p_1 - 1} p1−1p1a1+1−1 * p 2 a 2 + 1 − 1 p 2 − 1 \frac{p_2^{a_2 + 1} - 1}{p_2 - 1} p2−1p2a2+1−1 * … * p n a n + 1 − 1 p n − 1 \frac{p_n^{a_n + 1} - 1}{p_n - 1} pn−1pnan+1−1
内层循环中,若i % prime[j] != 0,此时i和prime[j]互素,易得 f [ i ∗ p r i m e [ j ] ] = f [ i ] ∗ f [ p r i m e [ j ] f[i * prime[j]] = f[i] * f[prime[j] f[i∗prime[j]]=f[i]∗f[prime[j]
而若i % prime[j] == 0,此时:
f [ i ] = f[i] = f[i]= p 1 a 1 + 1 − 1 p 1 − 1 \frac{p_1^{a_1 + 1} - 1}{p_1 - 1} p1−1p1a1+1−1 * p 2 a 2 + 1 − 1 p 2 − 1 \frac{p_2^{a_2 + 1} - 1}{p_2 - 1} p2−1p2a2+1−1 * … * p n a n + 1 − 1 p n − 1 \frac{p_n^{a_n + 1} - 1}{p_n - 1} pn−1pnan+1−1
f [ i ∗ p r i m e [ j ] ] = f[i * prime[j]] = f[i∗prime[j]]= p 1 a 1 + 2 − 1 p 1 − 1 \frac{p_1^{a_1 + 2} - 1}{p_1 - 1} p1−1p1a1+2−1 * p 2 a 2 + 1 − 1 p 2 − 1 \frac{p_2^{a_2 + 1} - 1}{p_2 - 1} p2−1p2a2+1−1 * … * p n a n + 1 − 1 p n − 1 \frac{p_n^{a_n + 1} - 1}{p_n - 1} pn−1pnan+1−1
我们可以很容易发现 f [ i ] f[i] f[i]与 f [ i ∗ p r i m e [ j ] ] f[i * prime[j]] f[i∗prime[j]]之间的区别:
f [ i ∗ p r i m e [ j ] ] = f[i * prime[j]] = f[i∗prime[j]]= f [ i ] / f[i] / f[i]/ p 1 a 1 + 1 − 1 p 1 − 1 \frac{p_1^{a_1 + 1} - 1}{p_1 - 1} p1−1p1a1+1−1 * p 1 − 1 p 1 a 1 + 1 − 1 \frac{p_1 - 1}{p_1^{a_1 + 1} - 1} p1a1+1−1p1−1 ,约分,再进行整理得到:
f[i * prime[j]] = f[i] / (pow(prime[j], cnt[i] + 1) - 1) * (pow(prime[j], cnt[i] + 2) - 1);
至此,代码就讲完了(LeTex写数学公式,累死了Wuu~)
五 完整代码
第1题 求因数个数
#include 第2题 求因数总和
#include 第二题中,需要注意的是:我们要求亲和数的和,所以在得到每个数字的真因数和之后,我们要判断f[f[i]] == i是否成立,这里要注意有一个数组非法访问的Bug,比如:f[9990] = 17370,这是我们若判断f[17370] = 9990, 此时访问数组大小只有10000的情况下,一定会非法访问,出现段错误,因此,我们在程序中稳妥起见,将数组开到了100000,这样就不会出错
至此,整个文章到这里也就结束了
六 题外话
- 话说,写Blog真是消耗时间,小编写这篇博客,写了一晚上加一上午才写完,我太南了。。。。。
- 鼓励自己,加油,你是最胖的!!!!!!与君共勉!!!