NOIP2012 提高组复赛解题报告

NOIP2012 提高组复赛

---

day1

1002. game

• 状态压缩dp
• 贪心（+高精度）

因为意识到本题做法必然是定义一个玄学的比较顺序，然后整个序列sort一波即可，所以我没敢直接写。毕竟自己遇到这种题目就出现问题，而且在思考的半小时中也没有搜刮到合理的贪心方法和证明（实际上只是因为我忘记以前写过的这类贪心该如何证明，估计是被上次ACM镜像赛上的有一题恶心到了）。最后没办法只好在敲好随机化之后，去敲第三题了（事实证明这个策略是对的，第三题异常水）。

最后的时候我尴尬地发现随机化部分不需要高精。而且由于第一次敲高精除感觉出了点问题。所以最后只水了40分。

这一题出的问题感觉比较难避免吧。既然知道自己已经想不到暴力就应该稳住部分分，结果好高骛远敲了高精。不应该啊。

对于 n≤10 的数据，我们采用全排列暴力，时间复杂度 O(n⋅n!) 。

【探索本条线路获得物品：随机化】通过利用上述暴力程序进行对拍，我们会发现对于当前的数据，构成最优解的序列非常多。这点是随机化60分的基础。

对于 n≤20 的数据，我们采用状态压缩dp，时间复杂度为 O(n⋅2n) 。具体实现是用二进制表示第i个大臣是否在目前序列中，得到转移方程式：

dp[S∣2i]=min(dp[S∣2i],max(dp[S],sum[S]r[i]))

/* 40分 状压dp写法 */
static const int S=20;
long long sum[1<1<#define fi first
#define se second
pair<int,int> s[S+5];
int main(){
    int n;
    scanf("%d",&n);
    if(n>20)exit(0);
    for(int i=0;i<=n;i++)
        scanf("%d %d",&s[i].fi,&s[i].se);
    for(int k=0;k<(1<0].fi;
        for(int i=0;iif(k>>i&1)sum[k]*=s[i+1].fi;
    }
    clear(dp,0x3f);
    int Allset=(1<1;
    dp[0]=0;
    for(int k=0;k<(1<1;k++)
        for(int i=0;iif(!(k>>i&1))dp[k|1<1<1].se));
    cout<

接下来还会发现一个显而易见的性质：

• 对于元素i的前面 [0,i−1] ， ∏i−1j=0l[j] 不会因为 [1,i−1] 的排序和元素i的选择产生影响。

说的深入点，就是对于两个相近元素的交换，只会对小范围内的最优解产生影响。根据这点有两种思路方向：

• 思路1：这种性质和冒泡排序类似，小范围的改变会逐渐地使答案靠近最优，并且与前面所做的选择无关。于是我们采用冒泡排序对序列进行不断交换。时间复杂度为 O(n2) ，预计得分60分。
• 思路2：由于序列满足“前无向性”，因此基于前面的最优解，我们需要让当前相邻两个元素也达到最优。于是开始推论相邻两个元素的关系。

正解的思路基于相邻交叉排序策略：

• 对于前面已经不会发生改变的最优解，解出后续相邻元素 {a,b} 接到该最优解后，仍然使得序列最优的条件式。通过该条件式可以对序列进行排序。

本题的结论是为了 {a,b} 顺序更优，有 l[a]⋅r[a]<l[b]⋅r[b] 。下面有两种均不严谨（均没有考虑向下取整这一条件——虽然即使不考虑也不会有问题。当然跪求大神严谨证明）的证法：

• 证法1（相邻交叉排序策略）：设在中间序列中取出 a,b ，此时前面序列 T=∏posi=1l[i] 。为了使得 {a,b} 的顺序比 {b,a} 优，有：

  {a,b}{b,a}:max{⌊Tr[a]⌋,⌊T⋅l[a]r[b]⌋}→max{T×r[b],T×(l[a]×r[a])}:max{⌊Tr[b]⌋,⌊T⋅l[b]r[a]⌋}→max{T×r[a],T×(l[b]×r[b])}

  由于保证 l[i],r[i](i∈[1,n])>0 ，所以上述式子就化简为比较 T×(l[a]⋅r[a]) 与 T×(l[b]⋅r[b]) 的大小。易知为了满足最优，必须有 l[a]⋅r[a]<l[b]⋅r[b] 。命题得证。

• 证法2（意识流证法）：显然，所有人的左手权值积是固定的，我们考虑最后一个元素的情况。为了使它为最优解，必然有 ⌊∏ni=0l[i]l[n]⋅r[n]⌋ 最小。同理对于 [1,i] 中的第i位，我们也类比如上证法。于是我们就按照 l[i]⋅r[i] 排序即可。

  好像两者乘积最大并不一定放在最后，但是我们根据上述打表内容，可以说将乘积最大的放在最后一定是最优解中的一种情况。于是命题得证。

之后根据数据大小以及60分处的提示，我们意识到要进行高精计算。对于高精除部分，如果是高精之间转化，则可以考虑采用二分答案实现；但是注意到数据大小为 ai≤104 ，如果是用万进制实现的高精度，我们可以实现高精与低精之间的运算。

最后时间复杂度为 O(nlogn→n2) 。

Code：

#include 
#include 
#include 
#include 
using namespace std;
char str[1005];
struct BigInt{
    static const int M=1005,P=10000;
    #define clear(x,val) memset(x,val,sizeof(x))
    int num[M],len;
    BigInt(){clear(num,0),len=1;}
    void print(){
        printf("%d",num[len-1]);
        for(int i=len-2;i>=0;i--)printf("%04d",num[i]);
        putchar('\n');
    }
    bool operator < (const BigInt &cmp)const{
        if(len!=cmp.len)return lenfor(int i=len-1;i>=0;i--)
            if(num[i]!=cmp.num[i])return num[i]return false;
    }
    BigInt operator + (const int &p){
        BigInt B;B=*this;
        B.num[0]+=p;
        int step=0;
        while(B.num[step]>=P){
            B.num[step+1]++;
            B.num[step]-=P;
            ++step;
        }
        while(B.num[B.len])++B.len;
        return B;
    }
    BigInt operator * (const int &p){
        BigInt B;
        B.len=len;
        for(int i=0;iif(B.num[i]>=P){
                B.num[i+1]+=B.num[i]/P;
                B.num[i]%=P;
            }
        }
        while(B.num[B.len])++B.len;
        return B;
    }
    BigInt operator / (const int &p){
        BigInt B=*this;
        for(int i=B.len-1;i>=0;i--){
            if(i)B.num[i-1]+=B.num[i]%p*P;
            B.num[i]/=p;
        }
        while(B.len>1&&!B.num[B.len-1])--B.len;
        return B;
    }
};
struct node{
    int a,b;
    bool operator < (const node &cmp)const{
        return a*b1005];
int main(){
    int n;
    scanf("%d",&n);
    for(int i=0;i<=n;i++)
        scanf("%d %d",&s[i].a,&s[i].b);
    sort(s+1,s+n+1);
    BigInt ans,pre,val;
    pre=pre+s[0].a;
    for(int i=1;i<=n;i++){
        val=pre/s[i].b;
        if(ans

1003. drive

• 倍增法

题目的复杂程度是和第三题相配的，但是难度就对不上了……或许只是因为做过比它更难的问题我才会这么想吧。其实两部分的优化我都想到了。但是我就是想A第二题。

现在想想我当时确实挺智障的。

本题题面比较杂，先整理一下题目大意：

【目标】对于给定的起点和最大长度，求出A，B分别行驶的路径长度。

【行驶方法】A，B为交替行驶，且小A先开车。其中A将会行驶到以该点作为出发点，向右第二近的城市，而B则为向右最近的城市。

【终止条件】当经过总路程长度 > 限制路径长度，或者接下来城市不存在第一/二近城市时，他们终止旅行。

城市远近的比较规则：

• 第一维按照 dis<st,gt>=|hst−hgt| 从小到大选择。
• 第二维按照海拔高度 hi 从小到大选择。

本题中比值定义：只要 distA=0 ， ans=∞ ，否则 ans=distBdistA 。

本题与POI2010_Frog非常相像。本题只需要完成两个操作：快速判断下个到达的城市和模拟两人的行驶。

如何在低复杂度判断下个到达的城市？

有这样一个性质：

• 每个城市接下来第一近和第二近的城市都是唯一确定的，与到达该城市前的城市无关。而且只有以下两个城市不存在解：第n-1号城市不存在第二近城市，第n号城市不存在第一/二近城市。

于是这个东西我们可以预处理出来。对于70分的数据，我们可以直接 O(n2) 暴力扫出来，更深入一点的话就需要处理下标问题常见的set，或者正解链表 O(n) （不考虑排序）（用法在NOIP2016提高组初赛中有出现过）。

然后就是顺便维护次值，这个问题也是POI2015_Trzy_wieże的弱化版。

如何低复杂度模拟两人的行驶？

对于每一个询问，我们都可以进行暴力 O(n) 跳跃，这个实现比较简单。由于上述每个城市的下一个抵达城市是确定的，所以我们可以处理出行驶 2k 次后到达的城市，以及A，B两人行驶的路程。于是我们采用倍增法进行跳跃。

当然这里处理倍增法比较麻烦，因为A，B是交错跳跃的。我的方法是特别处理跳一步的情况，因为之后就会换人跳，但是对于跳 2k(k≠1) 步的情况，下一个重新开始的人都是相同的。

综上，本题时间复杂度为 O(nlogn) 。

Code：

#include 
#include 
#include 
#include 
#include 
#define clear(x,val) memset(x,val,sizeof(x))
using namespace std;
template <class temp>
inline void Rd(temp &res){
    res=0;char c;int f=1;
    while(c=getchar(),c<48&&c!='-');
    do if(c=='-')f=-1;
    else res=(res<<3)+(res<<1)+(c^48);
    while(c=getchar(),c>47);
    res*=f;
}
template <class temp>
inline void Pn(temp res){
    if(!res)return;
    Pn(res/10);
    putchar(res%10^48);
}
template <class temp>
inline void Pf(temp res){
    if(!res)putchar('0');
    else Pn(res);
}
template <class temp>
inline temp _abs(temp a){
    return a<0?-a:a;
}

static const int S=17,N=100005,inf=0x3f3f3f3f;
int n,near[2][N];
long long h[N];
bool compy(long long h1,long long h2,long long h){//h1优于h2 
    if(_abs(h1-h)!=_abs(h2-h))return _abs(h1-h)<_abs(h2-h);
    return h1void up(int pos,int move){
    if(!~near[0][pos]){near[0][pos]=move;return;}

    if(compy(h[move],h[near[0][pos]],h[pos])){
        near[1][pos]=near[0][pos];
        near[0][pos]=move;
    }else if(!~near[1][pos]||compy(h[move],h[near[1][pos]],h[pos]))
        near[1][pos]=move;
}

typedef pair<long long,long long> pll;
pll dp[S][N];
#define fi first
#define se second
int nxt[S][N];
void init(){
    for(int i=1;i<=n;i++)
        if(~near[1][i]){
            nxt[1][i]=near[0][near[1][i]];
            if(~nxt[1][i]){
                dp[1][i].se=_abs(h[i]-h[near[1][i]]);
                dp[1][i].fi=_abs(h[near[1][i]]-h[nxt[1][i]]);
            }
        }else nxt[1][i]=-1;
    for(int k=1;k+1for(int i=1;i<=n;i++)
            if(~nxt[k][i]){
                nxt[k+1][i]=nxt[k][nxt[k][i]];
                if(~nxt[k+1][i]){
                    dp[k+1][i].fi=dp[k][i].fi+dp[k][nxt[k][i]].fi;
                    dp[k+1][i].se=dp[k][i].se+dp[k][nxt[k][i]].se;
                }
            }else nxt[k+1][i]=-1;
}
//小B cur=0  小A cur=1
long long val[2];
void calc(int st,long long xmax){
    clear(val,0);
    for(int k=S-1;k>0;k--)
        if(~nxt[k][st]&&val[1]+val[0]+dp[k][st].fi+dp[k][st].se<=xmax){
            val[0]+=dp[k][st].fi;
            val[1]+=dp[k][st].se;
            st=nxt[k][st];
        }
    if(~near[1][st]&&_abs(h[st]-h[near[1][st]])+val[1]+val[0]<=xmax)
        val[1]+=_abs(h[st]-h[near[1][st]]);
}

typedef pair<int,int> pii;
settable;
int main(){
    Rd(n);
    for(int i=1;i<=n;i++){
        Rd(h[i]);
        table.insert(make_pair(h[i],i));
    }

    clear(near,-1);
    set::iterator it,ite,ita;
    for(int i=1,cnt;i2;
        while(cnt--&&ite!=table.begin()){--ite;up(i,ite->second);}
        cnt=2;
        while(cnt--&&ita!=--table.end()){++ita;up(i,ita->second);}
        table.erase(it);
    }

    init();

    long long x0;Rd(x0);
    int pos=0;
    double bizhi=inf;
    for(int i=1;i<=n;i++){
        calc(i,x0);
        if(val[0]==0)continue;
        if(bizhi>1.0*val[1]/val[0]){
            bizhi=1.0*val[1]/val[0];
            pos=i;
        }else if(bizhi==1.0*val[1]/val[0]&&h[pos]printf("%d\n",pos);

    int m;Rd(m);
    for(int i=1;i<=m;i++){
        int st;
        long long xmax;
        Rd(st),Rd(xmax);
        calc(st,xmax);
        Pf(val[1]);putchar(' ');
        Pf(val[0]);putchar('\n');
    }
}

---

day2

1004. mod

• 扩展欧几里得算法

详见我前面两篇有关同余方程和扩展欧几里得的文章。

#include 
void exgcd(int a,int b,int &x,int &y){
    if(!b){x=1,y=0;return;}
    exgcd(b,a%b,y,x);
    y-=(a/b)*x;
}
int main(){// ll 文件 内存 变量 取模
    int a,b,x,y;
    scanf("%d %d",&a,&b);
    exgcd(a,b,x,y);
    x=(1ll*x%b+b)%b;
    printf("%d\n",x);
}

1005. classroom

• 数据结构
• 二分答案（单调性）

惨遭线段树卡常。以后应该尽可能避免线段树的使用，还有对于数据范围一定要更敏感，简单题也不能松懈，在保证正确性下能够进行的优化一定要进行。

说实在没有意识到线段树常数这么大，能硬生生被卡掉。

本题要%这位大犇。

根据题意，我们立刻会想到这样一个算法：

• 判断当前区间的最小值是否不小于给定的值，并且还要区间删除这个给定的值。

于是能够进行区间更新和区间查询的数据结构就只有线段树了。但是标准的线段树模板是会被卡掉一个点的，原因在于相同的query和update导致常数翻倍。于是这题应当合并update与query，即查询的时候同时删除即可。

线段树的时间复杂度为 O(mlogn) （常数大）。

（有点为线段树这种数据结构感到悲哀了）

本题的单调性也非常明显：“到第i组订单能否分配教室”这个命题是符合单调性的。即对于每一次二分，我们都需要处理出分配到第i组订单后，目前教室的使用情况。由于上述的这个处理是离线的，我们借鉴最开始做区间问题的方法：“刷漆”——差分前缀和来完成。这个思路还基于重构（或者说推翻重来）的思想。单次差分前缀和的复杂度是 O(i+n) ，所以时间复杂度为 O(nlogm) （常数小）。

/* 100分 二分答案做法*/ 
#include 
#include 
#include 
#define M 1000005
#define clear(x,val) memset(x,val,sizeof(x))
using namespace std;
template 
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48); 
    while(c=getchar(),c>47);
}
int a[M];
long long sum[M];
struct query{
    long long dis;
    int st,gt;
}q[M];
int n,m;
bool check(int p){
    clear(sum,0);
    for(int i=1;i<=p;i++)
        sum[q[i].st]-=q[i].dis,sum[q[i].gt+1]+=q[i].dis;
    for(int i=1;i<=n;i++){
        sum[i]+=sum[i-1];
        if(a[i]+sum[i]<0)return true;
    }
    return false;
}
int bisection(int L,int R){
    int res=-1;
    while(L<=R){
        int mid=L+R>>1;
        if(check(mid)){
            res=mid;
            R=mid-1;
        }else L=mid+1;
    }
    return res;
}
int main(){
    Rd(n),Rd(m);
    for(int i=1;i<=n;i++)Rd(a[i]);
    for(int i=1;i<=m;i++)Rd(q[i].dis),Rd(q[i].st),Rd(q[i].gt);
    int ans=bisection(1,m);
    if(!~ans)puts("0");
    else printf("-1\n%d\n",ans);
}

接下来我们需要以下发现：

• 对于每次的判断，我们都是累加 [1,i] 的所有情况，那么前面的元素就被多次重复累加了（加速算法的原因）。

• 对于 [1,k] 区间内的教室，如果检查到第j个订单，没有出现不够借出的情况，那么说明在检查第 [1,j−1] 个订单的时候，这段区间一定不会不够借出；同理如果出现不够借出的情况，那么对于接下来 [j+1,m] 的订单也一定不能满足。总结上述的话，就是：原序列的前缀序列也满足单调性。

• 对于同一个序列上的 a<b ，设 ti 为当前 [1,i] 区间能坚持到第 ti 个订单，则一定有 ta≥tb 。

那么于是把所有状态先丢进差分前缀和中，如果 [1,i] 不能坚持目前的状态，就不断回撤之前做过的抉择——将状态 ≥ta 的订单撤销掉。这样我们就可以不断递推得到这个 tn ，而不必进行二分答案求这个 tm 了。

上面%的那位大神说的有句话似乎点明主旨：

将离线的二分答案改为在线做法，就是将二分答案转化为线性复杂度的方法之一。

Code：

#include 
#include 
#include 
#define M 1000005
using namespace std;
template 
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48); 
    while(c=getchar(),c>47);
}
int a[M];
long long sum[M];
struct query{
    long long dis;
    int st,gt;
}q[M];
int n,m;
int main(){
    Rd(n),Rd(m);
    for(int i=1;i<=n;i++)Rd(a[i]);
    for(int i=1;i<=m;i++){
        Rd(q[i].dis),Rd(q[i].st),Rd(q[i].gt);
        sum[q[i].st]-=q[i].dis,sum[q[i].gt+1]+=q[i].dis;
    }
    int tot=m;
    for(int i=1;i<=n;i++){
        sum[i]+=sum[i-1];
        while(tot&&a[i]+sum[i]<0){
            if(i<=q[tot].gt){
                sum[max(i,q[tot].st)]+=q[tot].dis;
                sum[q[tot].gt+1]-=q[tot].dis;
            }
            --tot;
        }
    }
    if(tot==m)puts("0");
    else printf("-1\n%d\n",tot+1);
}

1006. blockade

• 二分答案+堆贪心

感觉本题的锅是我没有理顺堆贪心那一块部分。尤其是没有理清楚哪些点可以去更新而哪些不能，所以导致有一些情况没有考虑到。

啊，堆贪心真难。

本题的目标是求出最小的时间，使得所有军队在这个时间限制下，可以将所有叶子节点覆盖掉，即要求行走最远的军队所花时间最小。所以按照题目描述几乎可以确定，本题的思路是二分答案。

本题有以下贪心思路：

如果当前军队个数少于根节点儿子个数，说明无法控制疫情。（这一条可以直接判掉无解的情况）

对于一棵树，如果占据它的根节点，则这棵子树下的所有叶子节点都可以被覆盖。

那么哪些军队该去支援其他子树呢？我的贪心是：在保证当前子树被完全覆盖的前提下（其实甚至不一定要保证当前子树被完全覆盖），至少留下一人在根（神TM知道我怎么想的），其他贡献更多的军队去支援。于是只有70分。

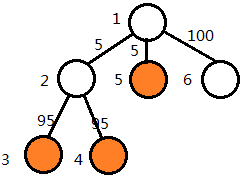
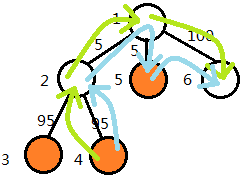
譬如说有这样一组数据（官方数据blockade2.in）：

→

答案为105，此时要求4号点补到5号点位置，5号点补到6号点位置，即蓝色线路。

这个图就是上述贪心的反例之一了。

感谢Kyle大犇帮我总结思路！

我们将点分成两组：能够跳出子树的点和不能跳出子树的点。

显然对于不能跳出的点，我们就把它最后跳到的位置mark一下，表示这个点以下的子树有军队覆盖。而能够跳出的点，就只需要记录那个跳到根上后，剩余时间最少的点。其他点扔进可以接下来贪心的堆中。

此时有两种特殊情况，仍然可以让这个最小贡献点不必放在子树的根上：

• 除了这个最小贡献点之外，剩下的点（亦包括那些能跳到子树根节点但是不能跳到根节点的军队）能完全覆盖这棵子树的叶节点。
• 这个最小贡献点可以跳出又跳入（也就是说这个点还是可以回来的，此时这个最小贡献点可能由其他点进来更优。这个贪心是均摊的思想，显然让一个点全走不如让多个点共同分担）

剩下的点就只能放在子树根节点了。

根据上述的贪心，我们只需要将没有完全匹配的点和多余的军队匹配一下就好了。显然按照花费时间从大到小匹配，当遇到无法匹配的时候，说明无解。

时间复杂度为 O(nlog2n) ，正好适合这个数据范围。

Code：

#include 
#include 
#include 
#include 
#include 
#include 
#define clear(x,val) memset(x,val,sizeof(x))
using namespace std;
template <class temp>
inline void Rd(temp &res){
    res=0;char c;
    while(c=getchar(),c<48);
    do res=(res<<3)+(res<<1)+(c^48);
    while(c=getchar(),c>47);
}
typedef long long LL;
static const int M=50005,inf=0x3f3f3f;
//-----------------------------
int n,m,head[M],etop=0;
#define root 1
struct node{int v,w,nxt;}Edges[M<<1];
void add_edge(int u,int v,int w){
    Edges[++etop]=(node){v,w,head[u]};head[u]=etop;
    Edges[++etop]=(node){u,w,head[v]};head[v]=etop;
}
LL dis[M];
int fa[M],army[M];
//-----------------------------
void dfs(int u,int pre,LL d){
    dis[u]=d;
    fa[u]=pre;
    for(int j=head[u];~j;j=Edges[j].nxt){
        node now=Edges[j];
        if(now.v!=pre)dfs(now.v,u,d+now.w);
    }
}
bool used[M];
struct cmp{
    bool operator()(int &a,int &b)const{return dis[a]int rest[M];
bool dfs_check(int u,int pre,bool flag){//当前有flag或者下面所有子树内有flag 
    if(flag)return true;
    bool f=false;
    for(int j=head[u];~j;j=Edges[j].nxt){
        int v=Edges[j].v;
        if(v==pre)continue;
        f=true;
        if(!dfs_check(v,u,flag|used[v]))return false;
    }
    return f;
}
bool check(int _time){
    clear(used,0);
    clear(rest,-1);
    priority_queue<int>q1;
    priority_queue<int,vector<int>,cmp>q2;
    for(int i=1;i<=m;i++){
        int u=army[i];
        while(fa[u]&&fa[u]!=root&&dis[army[i]]-dis[fa[u]]<=_time)u=fa[u];

        if(fa[u]!=root||_timetrue;
        else{
            int val=_time-dis[army[i]];
            if(!~rest[u])rest[u]=val;
            else{
                if(rest[u]>val)swap(rest[u],val);
                q1.push(val);
            }
        }
    }

    for(int j=head[root];~j;j=Edges[j].nxt){
        int v=Edges[j].v;
        bool flag=(~rest[v])&&(dfs_check(v,root,used[v])||rest[v]>=dis[v]);
        if(flag)q1.push(rest[v]);
        else if(~rest[v])used[v]=true;
    }

    for(int j=head[root];~j;j=Edges[j].nxt){
        int v=Edges[j].v;
        if(!dfs_check(v,root,used[v]))q2.push(v);
    }

    while(!q1.empty()&&!q2.empty()){
        int v=q2.top();
        if(q1.top()>=dis[v]){
            used[v]=true;
            q1.pop(),q2.pop();
        }else q1.pop();
    }

    return dfs_check(root,0,false);
}
int bisection(){
    int L=0,R=inf,res=-1;
    while(L<=R){
        int mid=L+R>>1;
        if(check(mid)){
            res=mid;
            R=mid-1;
        }else L=mid+1;
    }
    return res;
}
int main(){// LL 文件 内存 变量 取模
    Rd(n);
    int cnt=0;
    clear(head,-1);
    for(int i=1,u,v,w;iif(cnt>m){puts("-1");return 0;}
    for(int i=1;i<=m;i++)Rd(army[i]);
    dfs(root,0,0);
    printf("%d\n",bisection());
}