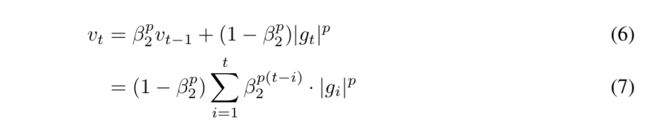ADAM : A METHOD FOR STOCHASTIC OPTIMIZATION
文章目录
- 概
- 主要内容
- 算法
- 选择合适的参数
- 一些别的优化算法
- AdaMax
- 理论
- 代码
Kingma D P, Ba J. Adam: A Method for Stochastic Optimization[J]. arXiv: Learning, 2014.
@article{kingma2014adam:,
title={Adam: A Method for Stochastic Optimization},
author={Kingma, Diederik P and Ba, Jimmy},
journal={arXiv: Learning},
year={2014}}
概
鼎鼎大名.
主要内容
用 f ( θ ) f(\theta) f(θ)表示目标函数, 随机最优通常需要最小化 E ( f ( θ ) ) \mathbb{E}(f(\theta)) E(f(θ)), 但是因为每一次我们都取的是一个小批次, 故实际上我们处理的是 f 1 ( θ ) , … , f T ( θ ) f_1(\theta),\ldots, f_T(\theta) f1(θ),…,fT(θ). 用 g t = ∇ θ f t ( θ ) g_t=\nabla_{\theta}f_t(\theta) gt=∇θft(θ)表示第 t t t步对应的梯度.
Adam 方法分别估计梯度 E ( g t ) \mathbb{E}(g_t) E(gt)的一阶矩和二阶矩(Adam: adaptive moment estimation 名字的由来).
算法
注意: 下面的算法中关于向量的运算都是逐项(element-wise)的运算.

选择合适的参数
首先, 分析为什么会有
m ^ t ← m t / ( 1 − β 2 t ) , v ^ t ← v t / ( 1 − β 2 t ) . (A.1) \tag{A.1} \hat{m}_t \leftarrow m_t / (1-\beta_2^t), \\ \hat{v}_t \leftarrow v_t / (1-\beta_2^t). m^t←mt/(1−β2t),v^t←vt/(1−β2t).(A.1)
可以用归纳法证明
m t = ( 1 − β 1 ) ∑ i = 1 t β 1 t − i ⋅ g i v t = ( 1 − β 2 ) ∑ i = 1 t β 2 t − i ⋅ g i 2 . (A.2) \tag{A.2} m_t = (1-\beta_1) \sum_{i=1}^t \beta_1^{t-i} \cdot g_i \\ v_t = (1-\beta_2) \sum_{i=1}^t \beta_2^{t-i} \cdot g_i^2. mt=(1−β1)i=1∑tβ1t−i⋅givt=(1−β2)i=1∑tβ2t−i⋅gi2.(A.2)
倘若分布稳定: E [ g t ] = E [ g ] , E [ g t 2 ] = E [ g 2 ] \mathbb{E}[g_t]=\mathbb{E}[g],\mathbb{E}[g_t^2]=\mathbb{E}[g^2] E[gt]=E[g],E[gt2]=E[g2], 则
E [ m t ] = E [ g ] ⋅ ( 1 − β 1 t ) E [ v t ] = E [ g 2 ] ⋅ ( 1 − β 2 t ) . (A.3) \tag{A.3} \mathbb{E}[m_t]=\mathbb{E}[g] \cdot(1-\beta_1^t) \\ \mathbb{E}[v_t]= \mathbb{E}[g^2] \cdot (1- \beta_2^t). E[mt]=E[g]⋅(1−β1t)E[vt]=E[g2]⋅(1−β2t).(A.3)
这就是为什么会有(A.1)这一步.
Adam提出时的一个很大的应用场景就是dropout(正对梯度是稀疏的情况), 这是往往需要我们取较大的 β 2 \beta_2 β2(可理解为抵消随机因素).
既然 E [ g ] / E [ g 2 ] ≤ 1 \mathbb{E}[g]/\sqrt{\mathbb{E}[g^2]}\le 1 E[g]/E[g2]≤1, 我们可以把步长 α \alpha α理解为一个信赖域(既然 ∣ Δ t ∣ < ≈ a |\Delta_t| \frac{<}{\approx} a ∣Δt∣≈<a).
另外一个很重要的性质是, 比如函数扩大(或缩小) c c c倍 c f cf cf, 此时梯度相应为 c g cg cg, 我们所对应的
c ⋅ m ^ t c 2 ⋅ v ^ t = m ^ t v ^ t , \frac{c \cdot \hat{m}_t}{\sqrt{c^2 \cdot \hat{v}_t}}= \frac{\hat{m}_t}{\sqrt{\hat{v}_t}}, c2⋅v^tc⋅m^t=v^tm^t,
并无变化.
一些别的优化算法
AdaGrad:
θ t + 1 = θ t − α ⋅ 1 ∑ i = 1 t g t 2 + ϵ g t . \theta_{t+1} = \theta_t -\alpha \cdot \frac{1}{\sqrt{\sum_{i=1}^tg_t^2}+\epsilon} g_t. θt+1=θt−α⋅∑i=1tgt2+ϵ1gt.
RMSprop:
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 θ t + 1 = θ t − α ⋅ 1 v t + ϵ g t . v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\ \theta_{t+1} = \theta_t -\alpha \cdot \frac{1}{\sqrt{v_t+\epsilon}}g_t. vt=β2vt−1+(1−β2)gt2θt+1=θt−α⋅vt+ϵ1gt.
AdaDelta:
v t = β 2 v t − 1 + ( 1 − β 2 ) g t 2 θ t + 1 = θ t − α ⋅ m t − 1 + ϵ v t + ϵ g t m t = β 1 m t − 1 + ( 1 − β 1 ) [ θ t + 1 − θ t ] 2 . v_t = \beta_2 v_{t-1} + (1-\beta_2) g_t^2 \\ \theta_{t+1} = \theta_t -\alpha \cdot \frac{\sqrt{m_{t-1}+\epsilon}}{\sqrt{v_t+\epsilon}}g_t \\ m_t = \beta_1 m_{t-1}+(1-\beta_1)[\theta_{t+1}-\theta_t]^2. vt=β2vt−1+(1−β2)gt2θt+1=θt−α⋅vt+ϵmt−1+ϵgtmt=β1mt−1+(1−β1)[θt+1−θt]2.
注: 均为逐项
AdaMax
本文还提出了另外一种算法
理论
不想谈了, 感觉证明有好多错误.
代码
import numpy as np
class Adam:
def __init__(self, instance, alpha=0.001, beta1=0.9, beta2=0.999,
epsilon=1e-8, beta_decay=1., alpha_decay=False):
""" the Adam using numpy
:param instance: the theta in paper, should have the grad method to call the grads
and the zero_grad method for clearing the grads
:param alpha: the same as the paper default:0.001
:param beta1: the same as the paper default:0.9
:param beta2: the same as the paper default:0.999
:param epsilon: the same as the paper default:1e-8
:param beta_decay:
:param alpha_decay: default False, if True, we will set alpha = alpha / sqrt(t)
"""
self.instance = instance
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
self.epsilon = epsilon
self.beta_decay = beta_decay
self.alpha_decay = alpha_decay
self.initialize_paras()
def initialize_paras(self):
self.m = 0.
self.v = 0.
self.timestep = 0
def update_paras(self):
grads = self.instance.grad
self.beta1 *= self.beta_decay
self.beta2 *= self.beta_decay
self.m = self.beta1 * self.m + (1 - self.beta1) * grads
self.v = self.beta2 * self.v + (1 - self.beta2) * grads ** 2
self.timestep += 1
if self.alpha_decay:
return self.alpha / np.sqrt(self.timestep)
return self.alpha
def zero_grad(self):
self.instance.zero_grad()
def step(self):
alpha = self.update_paras()
betat1 = 1 - self.beta1 ** self.timestep
betat2 = 1 - self.beta2 ** self.timestep
temp = alpha * np.sqrt(betat2) / betat1
self.instance.parameters -= temp * self.m / (np.sqrt(self.v) + self.epsilon)
class PPP:
def __init__(self, parameters, grad_func):
self.parameters = parameters
self.zero_grad()
self.grad_func = grad_func
def zero_grad(self):
self.grad = np.zeros_like(self.parameters)
def calc_grad(self):
self.grad += self.grad_func(self.parameters)
def f(x):
return x[0] ** 2 + 5 * x[1] ** 2
def grad(x):
return np.array([2 * x[0], 100 * x[1]])
if __name__ == "__main__":
x = np.array([10., 10.])
x = PPP(x, grad)
xs = []
ys = []
optim = Adam(x, alpha=0.4)
for i in range(100):
xs.append(x.parameters.copy())
y = f(x.parameters)
ys.append(y)
optim.zero_grad()
x.calc_grad()
optim.step()
xs = np.array(xs)
ys = np.array(ys)
import matplotlib.pyplot as plt
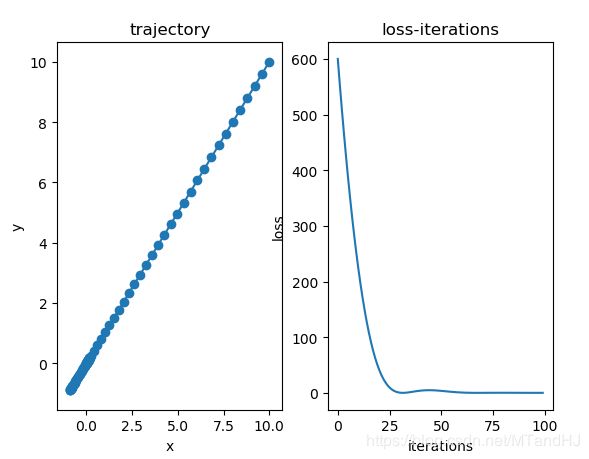
fig, (ax0, ax1)= plt.subplots(1, 2)
ax0.plot(xs[:, 0], xs[:, 1])
ax0.scatter(xs[:, 0], xs[:, 1])
ax0.set(title="trajectory", xlabel="x", ylabel="y")
ax1.plot(np.arange(len(ys)), ys)
ax1.set(title="loss-iterations", xlabel="iterations", ylabel="loss")
plt.show()