图的邻接矩阵存储结构基本操作的实现

主要代码：

/****************************************************
  @Title: 数据结构实验
  @Name: <实验7-1> 图的遍历
  @Object:
      [实验目的]
          实现图的存储结构；
          实现图的深度优先和广度优先遍历
      [实验提示]
          1. 在 graph.h 中实现图的基本操作
          2. 在 graph.h 中实现图的深度优先遍历和广度
             优先遍历           
  @Include:
      ds.h
          类C通用模块
      graph.h [*]
          图的实现
  @Usage:
      请查看"TO-DO列表",根据要求完成代码
  @Copyright: BTC 2004, Zhuang Bo
  @Author: Zhuang Bo
  @Date: 2004
  @Description:
*****************************************************/

#include 
#include  //for system()
#include "ds.h"
#include "graph.h"

Status printvex(VexType val); //访问顶点的函数 
void main()
{
    MGraph g;

    //建立图
    CreateGraph(g);
    //printf("\n邻接矩阵:\n"); 
    PrintAdjMatrix(g); //打印邻接矩阵 

    //深度优先和广度优先遍历图
    printf("\n深度优先遍历:\n"); 
    DFSTraverse(g,0,printvex); //从顶点0开始
    printf("\n广度优先遍历:\n"); 
    BFSTraverse(g,0,printvex);

    //销毁图
    DestroyGraph(g);    

    system("pause"); //暂停
}

//打印顶点 
Status printvex(VexType val)
{
    write(val);
    return OK;
}

/*
  Name: 图的邻接矩阵存储结构 
  Copyright: BTC 2004
  Author: Zhuang Bo
  Date: 2004
  Description: 
*/

#ifndef GRAPH_H_INCLUDED
#define GRAPH_H_INCLUDED
#define MAXQSIZE 64 
#include 
#include "ds.h"

///////////////////////////////////////////////////////////
//图的邻接矩阵表示
#define MAX_VERTEX_NUM 20 //最大顶点数
#define VexType char //顶点类型
#define ArcType int
#define INFINITY INT_MAX  //无穷大 
#define ElemType int
typedef struct {
    VexType  vexs[MAX_VERTEX_NUM]; //顶点向量 
    ArcType  arcs[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; //邻接矩阵 
    int      vexnum,arcnum;   //顶点,边个数
} MGraph;
typedef struct Sq{
    /* TODO (#1#): 这里完成循环队列的类型定义 */
    ElemType *base;
    int front;
    int rear;
    //....................................
} SqQueue;
int   visited[100];
/* 循环队列的最大容量 */

///////////////////////////////////////////////////////////
//图的基本操作声明 

//输入顶点和弧的信息，建立图
Status CreateGraph(MGraph &G); 
//销毁图的结构
Status DestroyGraph(MGraph &G);

//取顶点
VexType GetVex(MGraph G, int v);
//更新顶点信息 
Status PutVex(MGraph &G, int v, VexType val);
//插入弧(v,w)
Status InsertArc(MGraph &G, int v, int w, ArcType arc);
//删除弧(v,w)
Status DeleteArc(MGraph &G, int v, int w);
//插入顶点v
Status InsertVex(MGraph &G, VexType val);
//删除顶点v
Status DeleteVex(MGraph &G, int v);

//图G中顶点v的第一个邻接点
int FirstAdjVex(MGraph G, int v);
//图G中顶点v在w之后的下一个邻接点
int NextAdjVex(MGraph G, int v, int w);

//深度优先遍历图
void  DFSTraverse(MGraph G, int v, Status(*Visit)(VexType));
//广度优先遍历图 
Status BFSTraverse(MGraph G, int v, Status(*Visit)(VexType));

//打印邻接矩阵(调试用)
void PrintAdjMatrix(MGraph G);
int locateVex(MGraph G, VexType v);
void PrintAdjMatrix(MGraph G) ;
void DFS (MGraph G, int v);
Status InitQueue(SqQueue &Q);
EnQueue(SqQueue &Q, ElemType e);
Status QueueEmpty(SqQueue Q);
Status DeQueue(SqQueue &Q, ElemType &e);
///////////////////////////////////////////////////////////
//基本操作的实现
//删除队列Q的队头元素，并用e返回 
//  前提：队列Q存在且非空 
Status DeQueue(SqQueue &Q, ElemType &e)
{
    /* TODO (#9#): 出队列存入e */
    if(Q.front==Q.rear){
        return ERROR;
    }
    e=Q.base[Q.front];
    Q.front=(Q.front+1)%MAXQSIZE;
    return OK ;//返回操作状态(成功:OK,失败:ERROR)
    //....................................
}
//若队列Q为空，则返回TRUE，否则FALSE 
//  前提：队列Q已存在
Status QueueEmpty(SqQueue Q)
{
    /* TODO (#5#): 判断队列是否为空 */
    if(Q.rear==Q.front){
        return TRUE; 
    }
    return FALSE;
    //....................................
}

//构造一个空队列Q
Status InitQueue(SqQueue &Q)
{
    /* TODO (#2#): 构造空队列 */
    Q.base=(ElemType*)malloc(MAXQSIZE*sizeof(ElemType));
    if(!Q.base){
        exit(0);
    }
    Q.front=Q.rear=0;
    return OK; //TODO: 替换这行代码,以下同
    //....................................
}
//入队列
Status EnQueue(SqQueue &Q, ElemType e)
{
    /* TODO (#8#): 元素e入队列 */
    if((Q.rear+1)%MAXQSIZE==Q.front){
        return ERROR;
    }
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXQSIZE;
    return OK;//返回操作状态(成功:OK,失败:ERROR)
    //....................................
}
int locateVex(MGraph G, VexType v){
    for(int i = 0; i < G.vexnum; i++){
        if(G.vexs[i] == v)
            return i;
    }
    return -1;//图中没有该顶点
}

//输入顶点和弧的信息，建立图
Status CreateGraph(MGraph &G)
{
    //-------------------------------------
    // TODO (#1#): 先输入顶点个数和顶点数据,然后输入弧，建立图 
    printf("输入顶点数和弧数如:(5,3):");
    scanf("%d,%d", &G.vexnum, &G.arcnum);

    printf("输入%d个顶点（以空格隔开如：v1 v2 v3）:", G.vexnum);
    getchar();//吃掉换行符
    for(int m = 0; m < G.vexnum; m++){
        scanf("%c", &G.vexs[m]);
        getchar();//吃掉空格符
    }
    for( m = 0; m < G.vexnum; m++){
        printf("%c", G.vexs[m]);
        printf("\n");
    //  getchar();//吃掉空格符
    }
//初始化邻接矩阵
    int i=0, j=0;
    for(i = 0; i < G.vexnum; i++){
        for(j = 0; j < G.vexnum; j++)
            G.arcs[i][j] = 0;
    }
//打印初始化的邻接矩阵

/*  for(i = 0; i < G.vexnum; i++){
        for(j = 0; j < G.vexnum; j++)
        printf( "%5d\n",G.arcs[i][j]);
    }*/
    VexType v1, v2;//分别是一条弧的弧尾和弧头（起点和终点）
    int w;//对于无权图或网，用0或1表示相邻否；对于带权图或网，则为相应权值    
    printf("\n每行输入一条弧依附的顶点（先弧尾后弧头）和权值（如：v1 v2 3）:\n");
    fflush(stdin);//清除残余后，后面再读入时不会出错
   for(int k = 0; k < G.arcnum; k++){
        scanf("%c %c %d",&v1, &v2, &w);
        fflush(stdin);//清除残余后，后面再读入时不会出错
        i = locateVex(G, v1);
        j = locateVex(G, v2);
        G.arcs[i][j] = w;
    }

    return OK;
    //-------------------------------------
}

//销毁图的结构
Status DestroyGraph(MGraph &G)
{
    return OK;//什么也不做
} 

//取顶点
Status GetVex(MGraph G, int v, VexType &val)
{
    if(v<0||v>=G.vexnum) return ERROR;
    val = G.vexs[v];
    return OK;
}

//更新顶点信息 
Status PutVex(MGraph &G, int v, VexType val)
{
    if(v<0||v>=G.vexnum) return ERROR;
    G.vexs[v] = val;
    return OK;
}

//插入弧(v,w)
Status InsertArc(MGraph &G, int v, int w, ArcType arc)
{
    if(v<0||v>=G.vexnum||w<0||w>=G.vexnum) return ERROR;
    G.arcs[v][w] = arc;
    return OK;
}

//删除弧(v,w)
Status DeleteArc(MGraph &G, int v, int w)
{
    if(v<0||v>=G.vexnum||w<0||w>=G.vexnum) return ERROR;
    G.arcs[v][w] = 0; //删除弧 
    return OK;
}

//插入顶点v
Status InsertVex(MGraph &G, VexType val)
{
    //-------------------------------------
    // TODO (#1#): 插入顶点v,注意对邻接矩阵的影响

    return ERROR;
    //-------------------------------------
}

//删除顶点v
Status DeleteVex(MGraph &G, int v)
{
    //-------------------------------------
    // TODO (#1#): 删除顶点v,注意对邻接矩阵的修改

    return ERROR;
    //-------------------------------------
}

//图G中顶点v的第一个邻接点，不存在时返回 -1 
int FirstAdjVex(MGraph G, int v)
{
    //-------------------------------------
    // TODO (#1#): 返回顶点v的第一个邻接点
    int i;
    for(i=0;iif(G.arcs[v][i]){
            return i;
        }
    }
    return -1;
    //-------------------------------------
}

//图G中顶点v在w之后的下一个邻接点，不存在时返回 -1
int NextAdjVex(MGraph G, int v, int w)
{
    //-------------------------------------
    // TODO (#1#): 返回顶点v在w之后的下一个邻接点
    int i;
    for(i=w+1;iif(G.arcs[v][i]){
            return i;
        }
    }
    return -1;
    //-------------------------------------
}
//深度优先遍历图
void DFSTraverse(MGraph G, int v, Status(*Visit)(VexType))
{

    //-------------------------------------
    // TODO (#1#): 从v出发，深度优先遍历图
    for(v=0;vfor(v=0;vif(!visited[v]){
           DFS (G, v);
        }
    }
    //-------------------------------------
}
void DFS (MGraph G, int v){
        visited[v]= TRUE;
        write (v);
           for(int w=FirstAdjVex(G, v);w>0;w=NextAdjVex(G, v, w)){
               if(!visited[w])
                    DFS (G, w);
           }
}
//广度优先遍历图 
Status BFSTraverse(MGraph G, int v, Status(*Visit)(VexType))
{
    //-------------------------------------
    // TODO (#1#): 从v出发，广度优先遍历图
    int u;
    SqQueue Q;
    for(v=0;vfor(v=0;vif(!visited[v]){
            visited[v]=TRUE;
            write (v);
            EnQueue(Q, v);
            while(!QueueEmpty(Q)){
                DeQueue(Q, u);
                for(int w=FirstAdjVex(G, u);w>=0;w=NextAdjVex(G, u, w))
                    if(!visited[w]){
                        visited[w]=TRUE;
                        write (w);
                        EnQueue(Q, w);
                    }

                }


    }
    //-------------------------------------
    return 1;
}

//打印邻接矩阵
void PrintAdjMatrix(MGraph G) 
{
    int i,j;
    for(i=0; ifor(j=0; j"%5d", G.arcs[i][j]);
        printf("\n");
    }
}

#endif //GRAPH_H_INCLUDED

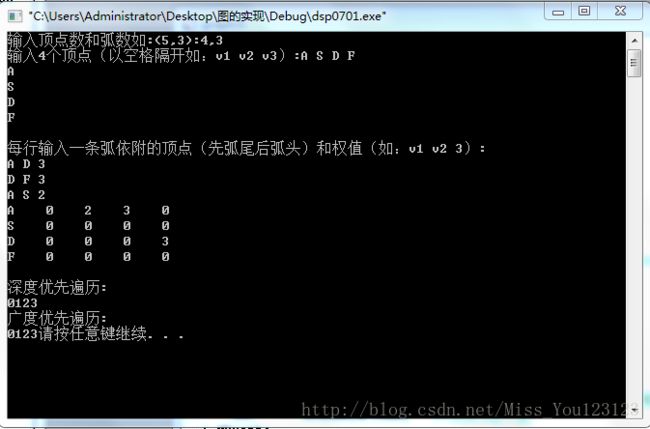
演示效果图：