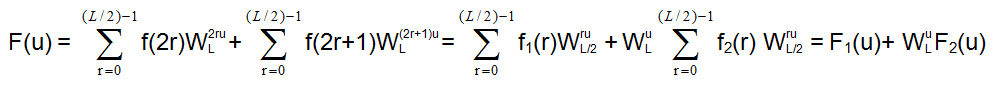C++实现一维快速傅里叶变换(FFT)

一维离散傅里叶变换的公式为：

如果直接基于该定义进行编程实现，则算法时间复杂度为O(N²)。具体的编程实现我们已经在《C++实现一维离散傅里叶变换》中介绍过了。

当一维信号长度达到几十万个信号时，当前主流4G主频CPU完成一次傅里叶变换需要约几十到几百秒的时间，这样的效率显然是让人无法接受的。

为了解决傅里叶变换的计算效率问题，行业专家们提出了蝶形算法，极大地提升了傅里叶变换的运算效率。

在蝶形算法中，较为流行的是基于时间抽取的基-2快速傅里叶变换算法（以下简称为基-2FFT算法）。

基-2FFT算法要求原始信号长度L=2^N，N为正整数。也就是说，信号长度必须为2的整数次方，如4、8、16、32、64、512、1024。这是由蝶形算法的二进分解性质决定的。

设原始信号序列为f(x)，长度为L（L=2 ^N，为2的整数次方），x=0,1,2,3,…,L-1，则傅里叶变换可表达为：

将f(x)按x的奇偶性分成两组：

则式1-1变为：

其中，F₁(u)和F₂(u)分别为f₁(x)和f₂(x)的(L/2)点的一维离散傅里叶变换。

例如，对于8个点的信号序列，可先分解两个长度为4的离散傅里叶变换，再将两个长度为4的离散傅里叶变换，各自分解为两个长度为2的离散傅里叶变换。故只需要计算4个长度为2的离散傅里叶变换，就可以递归算出原序列共8个点的dft。更为广泛地，对于长度为L=2^N个点的信号序列，只需要计算2^N-1个长度为2的离散傅里叶变换，就可以递归算出原序列共2^N个点的dft。

现在我们研究信号输入端的输入顺序和变换结果输出端的输出顺序的关系。

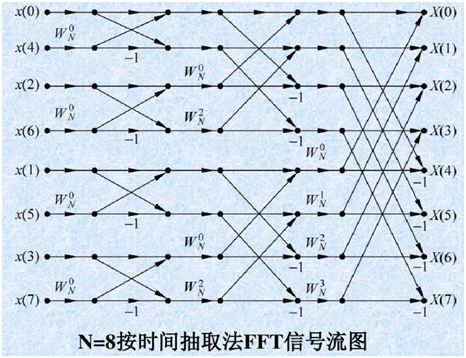
8点序列的蝶形运算流程图如下：

(图片来源自百度文库《05-第五章快速傅里叶变换(蝶形运算)》)

观察上图(最左边可视为f(x)，最右边视为F(x))，右边输出端的输出顺序为自然顺序，而最左边的输入端则并不是按自然顺序。这是因为序列f(x)在蝶形运算过程中被反复进行奇偶分解，对于长度为L=2^N的序列，共分解N-1次，每一次分解，都是按二进制码0和1进行奇偶排列。经观察，发现这是一种二进制码位的倒序重排，例如，对于8点的序列，其码位倒序图为：

(图片来源自百度文库《05-第五章快速傅里叶变换(蝶形运算)》)

至此，对于以2为基的快速傅里叶变换算法，我们可以构思出一条清晰的实现思路，具体如下：

1.根据序列长度L，计算出倒序的码位；

2.算出加权序列W(WuL，上下标打不出来)；

3. 计算2^N-1个长度为2的离散傅里叶变换；

4.基于前述的蝶形运算公式1-2和分解流程，递归算出原序列共2^N个点的dft。

至于逆变换，只需要按照上述思路进行逆向推导，即从结果逆推回到第一步，就可以得到自然序列的原始信号。

 

下面给出根据上述思路编写的FFT类头文件和实现文件：

Fft1.h

#pragma once

#define      MAX_MATRIX_SIZE                   4194304             // 2048 * 2048
#define      PI                                           3.141592653
#define      MAX_VECTOR_LENGTH              10000             //

typedef struct Complex
{
	double rl;
	double im;
}Complex;

class CFft1
{
public:
	CFft1(void);
	~CFft1(void);

public:
	bool fft(Complex IN const inVec[], int IN const len, Complex IN outVec[]);            // 基于蝶形算法的快速傅里叶变换
    bool ifft(Complex IN const inVec[], int IN const len, Complex IN outVec[]);

	bool is_power_of_two(int IN num);
	int    get_computation_layers(int IN num);         // calculate the layers of computation needed for FFT
};

Fft1.cpp

#include "stdafx.h"
#include "Fft1.h"

CFft1::CFft1()
{
}


CFft1::~CFft1()
{
}


bool CFft1::is_power_of_two(int IN num)
{
	int temp = num;
	int mod = 0;
	int result = 0;

	if (num < 2)
		return false;
	if (num == 2)
		return true;

	while (temp > 1)
	{
		result = temp / 2;
		mod = temp % 2;
		if (mod)
			return false;
		if (2 == result)
			return true;
		temp = result;
	}
	return false;
}


int CFft1::get_computation_layers(int IN num)
{
	int nLayers = 0;
	int len = num;
	if (len == 2)
		return 1;
	while (true) {
		len = len / 2;
		nLayers++;
		if (len == 2)
			return nLayers + 1;
		if (len < 1)
			return -1;
	}
}


// Fourier transform of 1 - dimension vector
// Param1: the input vector to be transformed
// Param 2: len of the input vector
// Param 3: output vector, which is the result of fft
bool CFft1::fft(Complex IN inVec[], int IN const vecLen, Complex IN outVec[])
{
	char msg[256] = "11111 ";

	if ((vecLen <= 0) || (NULL == inVec) || (NULL == outVec))
		return false;
	if (!is_power_of_two(vecLen))
		return false;

	// create the weight array
	Complex         *pVec = new Complex[vecLen];
	Complex         *Weights = new Complex[vecLen];
	Complex         *X = new Complex[vecLen];
	int                   *pnInvBits = new int[vecLen];

	memcpy(pVec, inVec, vecLen*sizeof(Complex));

	// 计算权重序列
	double fixed_factor = (-2 * PI) / vecLen;
	for (int i = 0; i < vecLen / 2; i++) {
		double angle = i * fixed_factor;
		Weights[i].rl = cos(angle);
		Weights[i].im = sin(angle);
	}
	for (int i = vecLen / 2; i < vecLen; i++) {
		Weights[i].rl = -(Weights[i - vecLen / 2].rl);
		Weights[i].im = -(Weights[i - vecLen / 2].im);
	}

	int r = get_computation_layers(vecLen);

	// 计算倒序位码
	int index = 0;
	for (int i = 0; i < vecLen; i++) {
		index = 0;
		for (int m = r - 1; m >= 0; m--) {
			index += (1 && (i & (1 << m))) << (r - m - 1);
		}
		pnInvBits[i] = index;
		X[i].rl = pVec[pnInvBits[i]].rl;
		X[i].im = pVec[pnInvBits[i]].im;
	}

	// 计算快速傅里叶变换
	for (int L = 1; L <= r; L++) {
		int distance = 1 << (L - 1);
		int W = 1 << (r - L);

		int B = vecLen >> L;
		int N = vecLen / B;

		for (int b = 0; b < B; b++) {
			int mid = b*N;
			for (int n = 0; n < N / 2; n++) {
				int index = n + mid;
				int dist = index + distance;
				pVec[index].rl = X[index].rl + (Weights[n*W].rl * X[dist].rl - Weights[n*W].im * X[dist].im);                      // Fe + W*Fo
				pVec[index].im = X[index].im + Weights[n*W].im * X[dist].rl + Weights[n*W].rl * X[dist].im;
			}
			for (int n = N / 2; n < N; n++) {
				int index = n + mid;
				pVec[index].rl = X[index - distance].rl + Weights[n*W].rl * X[index].rl - Weights[n*W].im * X[index].im;        // Fe - W*Fo
				pVec[index].im = X[index - distance].im + Weights[n*W].im * X[index].rl + Weights[n*W].rl * X[index].im;
			}
		}

		memcpy(X, pVec, vecLen*sizeof(Complex));
	}

	memcpy(outVec, pVec, vecLen*sizeof(Complex));
	if (Weights)      delete[] Weights;
	if (X)                 delete[] X;
	if (pnInvBits)    delete[] pnInvBits;
	if (pVec)           delete[] pVec;
	return true;
}


bool CFft1::ifft(Complex IN const inVec[], int IN const len, Complex IN outVec[])
{
	char msg[256] = "11111 ";

	if ((len <= 0) || (!inVec))
		return false;
	if (false == is_power_of_two(len)) {
		return false;
	}

	double         *W_rl = new double[len];
	double         *W_im = new double[len];
	double         *X_rl = new double[len];
	double         *X_im = new double[len];
	double         *X2_rl = new double[len];
	double         *X2_im = new double[len];

	double fixed_factor = (-2 * PI) / len;
	for (int i = 0; i < len / 2; i++) {
		double angle = i * fixed_factor;
		W_rl[i] = cos(angle);
		W_im[i] = sin(angle);
	}
	for (int i = len / 2; i < len; i++) {
		W_rl[i] = -(W_rl[i - len / 2]);
		W_im[i] = -(W_im[i - len / 2]);
	}

	// 时域数据写入X1
	for (int i = 0; i < len; i++) {
		X_rl[i] = inVec[i].rl;
		X_im[i] = inVec[i].im;
	}
	memset(X2_rl, 0, sizeof(double)*len);
	memset(X2_im, 0, sizeof(double)*len);

	int r = get_computation_layers(len);
	if (-1 == r)
		return false;
	for (int L = r; L >= 1; L--) {
		int distance = 1 << (L - 1);
		int W = 1 << (r - L);

		int B = len >> L;
		int N = len / B;
		//sprintf(msg + 6, "B %d, N %d, W %d, distance %d, L %d", B, N, W, distance, L);
		//OutputDebugStringA(msg);

		for (int b = 0; b < B; b++) {
			for (int n = 0; n < N / 2; n++) {
				int index = n + b*N;
				X2_rl[index] = (X_rl[index] + X_rl[index + distance]) / 2;
				X2_im[index] = (X_im[index] + X_im[index + distance]) / 2;
				//sprintf(msg + 6, "%d, %d: %lf, %lf", n + 1, index, X2_rl[index], X2_im[index]);
				//OutputDebugStringA(msg);
			}
			for (int n = N / 2; n < N; n++) {
				int index = n + b*N;
				X2_rl[index] = (X_rl[index] - X_rl[index - distance]) / 2;           // 需要再除以W_rl[n*W]
				X2_im[index] = (X_im[index] - X_im[index - distance]) / 2;
				double square = W_rl[n*W] * W_rl[n*W] + W_im[n*W] * W_im[n*W];          // c^2+d^2
				double part1 = X2_rl[index] * W_rl[n*W] + X2_im[index] * W_im[n*W];         // a*c+b*d
				double part2 = X2_im[index] * W_rl[n*W] - X2_rl[index] * W_im[n*W];          // b*c-a*d			
				if (square > 0) {
					X2_rl[index] = part1 / square;
					X2_im[index] = part2 / square;
				}
			}
		}
		memcpy(X_rl, X2_rl, sizeof(double)*len);
		memcpy(X_im, X2_im, sizeof(double)*len);
	}

	// 位码倒序
	int index = 0;
	for (int i = 0; i < len; i++) {
		index = 0;
		for (int m = r - 1; m >= 0; m--) {
			index += (1 && (i & (1 << m))) << (r - m - 1);
		}
		outVec[i].rl = X_rl[index];
		outVec[i].im = X_im[index];
		//sprintf(msg + 6, "X_rl[i]: %lf, %lf,  index: %d", out_rl[i], out_im[i], index);
		//OutputDebugStringA(msg);
	}

	if (W_rl)      delete[] W_rl;
	if (W_im)    delete[] W_im;
	if (X_rl)      delete[] X_rl;
	if (X_im)     delete[] X_im;
	if (X2_rl)     delete[] X2_rl;
	if (X2_im)    delete[] X2_im;

	return true;
}

现在，我们编写并运行一个测试线程，对一个16点的一维信号进行快速傅里叶变换，以验证上述代码。

DWORD WINAPI test(LPVOID lParam)
{
	double vec[] = { 15, 32, 9, 222, 118, 151, 5, 7, 56, 233, 56, 121, 235, 89, 98, 111 };
	int len = sizeof(vec) / sizeof(double);

	Complex *inVec = new Complex[len];
	Complex *outVec = new Complex[len];
	Complex *invert = new Complex[len];

	memset(inVec, 0, len*sizeof(Complex));
	for (int i = 0; i < len; i++)
		inVec[i].rl = vec[i];

	// Fourier transformation
	CFft1 t;
	t.fft(inVec, len, outVec);

	// print result
	char msg[256] = "11111 ";
	OutputDebugStringA("11111 快速傅里叶变换结果为：");
	for (int i = 0; i < len; i++) {
		if (outVec[i].im < 0)
			sprintf(msg + 6, "result[%d]: %lf - %lfi", i+1, outVec[i].rl, -outVec[i].im);
		else
			sprintf(msg + 6, "result[%d]: %lf + %lfi", i + 1, outVec[i].rl, outVec[i].im);
		OutputDebugStringA(msg);
	}

	OutputDebugStringA("11111 逆变换结果为：");
	t.ifft(outVec, len, invert);
	for (int i = 0; i < len; i++) {
		sprintf(msg + 6, "ifft[%d]: %lf", i + 1, invert[i].rl);
		OutputDebugStringA(msg);
	}

	delete[] inVec;
	delete[] outVec;
	delete[] invert;
	return 0;
}

在MFC对话框资源中添加一个test按钮，在按钮事件响应函数中添加：
::CreateThread(NULL,0, test, 0, 0, NULL);
然后编译项目。编译成功后，先打开DebugView日志观察工具，再启动生成的exe，点击test按钮，可以在DebugView中看到以下日志输出：

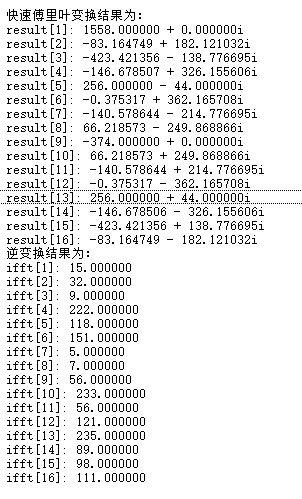
可以看到，逆变换的结果和原始信号完全一致。

使用Matlab的fft()函数对原始信号进行变换，得到的结果也和上述变换结果一致。

因此我们的实现代码是有效的，输出了正确的变换结果。