《Neural Architecture Search with Reinforcement Learning》翻译
原文:https://arxiv.org/abs/1611.01578
Neural Architecture Search with Reinforcement Learning
ABSTRACT
Neural networks are powerful and flexible models that work well for many diffi-cult learning tasks in image, speech and natural language understanding. Despitetheir success, neural networks are still hard to design. In this paper, we use a re-current network to generate the model descriptions of neural networks and trainthis RNN with reinforcement learning to maximize the expected accuracy of thegenerated architectures on a validation set. On the CIFAR-10 dataset, our method,starting from scratch, can design a novel network architecture that rivals the besthuman-invented architecture in terms of test set accuracy. Our CIFAR-10 modelachieves a test error rate of 3.65, which is 0.09 percent better and 1.05x faster thanthe previous state-of-the-art model that used a similar architectural scheme. Onthe Penn Treebank dataset, our model can compose a novel recurrent cell that out-performs the widely-used LSTM cell, and other state-of-the-art baselines. Our cellachieves a test set perplexity of 62.4 on the Penn Treebank, which is 3.6 perplex-ity better than the previous state-of-the-art model. The cell can also be transferredto the character language modeling task on PTB and achieves a state-of-the-artperplexity of 1.214.
带强化学习的神经结构搜索
摘要
神经网络是功能强大且灵活的模型,适用于图像,语音和自然语言理解等众多难度较大的学习任务。尽管他们取得了成功,神经网络仍然很难设计。在本文中,我们使用回流网络来生成神经网络的模型描述,并通过强化学习来训练这个RNN,以最大化生成的体系结构在验证集上的预期精度。在CIFAR-10数据集上,我们的方法从头开始,可以设计出一种新颖的网络架构,在测试集精度方面与最佳人造架构相媲美。我们的CIFAR-10模型的测试错误率为3.65,比使用类似架构方案的先前模型的测试错误率提高了0.09%和1.05倍。在Penn Treebank数据集上,我们的模型可以组成一个新型复发性细胞,它可以胜任广泛使用的LSTM细胞和其他最先进的基线。我们在宾夕法尼亚州立大学的课堂上对测试集的困惑度为62.4,比以前的最先进的模型要好3.6倍。单元也可以转移到PTB上的字符语言建模任务,并达到1.214的最新状态。
1 INTRODUCTION
The last few years have seen much success of deep neural networks in many challenging appli-cations, such as speech recognition (Hinton et al., 2012), image recognition (LeCun et al., 1998;Krizhevsky et al., 2012) and machine translation (Sutskever et al., 2014; Bahdanau et al., 2015; Wuet al., 2016). Along with this success is a paradigm shift from feature designing to architecturedesigning, i.e., from SIFT (Lowe, 1999), and HOG (Dalal & Triggs, 2005), to AlexNet (Krizhevskyet al., 2012), VGGNet (Simonyan & Zisserman, 2014), GoogleNet (Szegedy et al., 2015), andResNet (He et al., 2016a). Although it has become easier, designing architectures still requires alot of expert knowledge and takes ample time.
1引言
近几年来,在许多具有挑战性的应用中,如语音识别(Hinton等,2012),图像识别(LeCun等,1998; Krizhevsky等,2012),深度神经网络取得了很大的成功。 机器翻译(Sutskever等,2014; Bahdanau等,2015; Wuet等,2016)。 随着这一成功,从SIFT(Lowe,1999)和HOG(Dalal&Triggs,2005)到AlexNet(Krizhevskyet al。,2012),VGGNet(Simonyan&Zisserman, 2014),GoogleNet(Szegedy等,2015)和ResNet(He等,2016a)。 虽然它变得更容易,但设计架构仍需要大量专业知识并需要足够的时间。
Our experiments show that Neural Architecture Search can design good models from scratch, anachievement considered not possible with other methods. On image recognition with CIFAR-10,Neural Architecture Search can find a novel ConvNet model that is better than most human-inventedarchitectures. Our CIFAR-10 model achieves a 3.65 test set error, while being 1.05x faster than thecurrent best model. On language modeling with Penn Treebank, Neural Architecture Search candesign a novel recurrent cell that is also better than previous RNN and LSTM architectures. The cellthat our model found achieves a test set perplexity of 62.4 on the Penn Treebank dataset, which is3.6 perplexity better than the previous state-of-the-art.
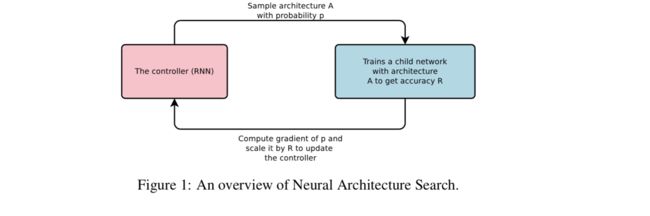
本文介绍了神经架构搜索(Neural Architecture Search),这是一种用于找到良好架构的基于梯度的方法(参见图1)。我们的工作基于这样的观察:神经网络的结构和连接性通常可以由可变长度的字符串来指定。因此可以使用经常性网络 - 控制器 - 来生成这样的字符串。训练由字符串指定的网络 - “子网” - 对真实数据的处理将导致验证集的准确性。使用这个精度作为奖励信号,我们可以计算策略梯度来更新控制器。因此,在下一次迭代中,控制器将为获得高精度的架构提供更高的概率。换句话说,控制器将学习随着时间的推移改进搜索。
我们的实验表明,神经架构搜索可以从头开始设计出好的模型,但不能用其他方法来实现。在用CIFAR-10进行图像识别时,神经架构搜索可以找到比大多数人类发明的建筑更好的新型ConvNet模型。我们的CIFAR-10模型实现了3.65测试集错误,比当前最佳模型快1.05倍。在与Penn Treebank进行语言建模时,Neural Architecture Search可以设计出一种比以前的RNN和LSTM体系结构更好的新颖复发单元。我们的模型发现的细胞在Penn Treebank数据集上达到了62.4的测试集困惑度,这比以前的先进水平要好3.6倍。
2 RELATED WORK
Hyperparameter optimization is an important research topic in machine learning, and is widely usedin practice (Bergstra et al., 2011; Bergstra & Bengio, 2012; Snoek et al., 2012; 2015; Saxena &Verbeek, 2016). Despite their success, these methods are still limited in that they only search modelsfrom a fixed-length space. In other words, it is difficult to ask them to generate a variable-lengthconfiguration that specifies the structure and connectivity of a network. In practice, these methodsoften work better if they are supplied with a good initial model (Bergstra & Bengio, 2012; Snoeket al., 2012; 2015). There are Bayesian optimization methods that allow to search non fixed lengtharchitectures (Bergstra et al., 2013; Mendoza et al., 2016), but they are less general and less flexiblethan the method proposed in this paper.
Modern neuro-evolution algorithms, e.g., Wierstra et al. (2005); Floreano et al. (2008); Stanley et al.(2009), on the other hand, are much more flexible for composing novel models, yet they are usuallyless practical at a large scale. Their limitations lie in the fact that they are search-based methods,thus they are slow or require many heuristics to work well.
2相关工作
超参数优化是机器学习中的一个重要研究课题,在实践中被广泛应用(Bergstra et al。,2011; Bergstra&Bengio,2012; Snoek et al。,2012; 2015; Saxena&Verbeek,2016)。尽管他们取得了成功,但这些方法仍然有限,因为他们只能从固定长度的空间搜索模型。换句话说,要求他们生成一个规定网络结构和连接性的可变长度配置是很困难的。在实践中,如果这些方法提供了良好的初始模型(Bergstra&Bengio,2012; Snoeket等,2012; 2015),这些方法往往会更好地工作。有贝叶斯优化方法可以用来搜索非固定尺寸的建筑物(Bergstra等,2013; Mendoza等,2016),但与本文提出的方法相比,它们不那么一般和灵活。
现代神经进化算法,例如Wierstra等人(2005年); Floreano等人(2008);另一方面,斯坦利等人(2009)在组成新模型方面更加灵活,然而它们在大规模时是无法实用的。它们的局限性在于它们是基于搜索的方法,因此它们很慢或需要许多启发式才能运行良好。
Neural Architecture Search has some parallels to program synthesis and inductive programming, theidea of searching a program from examples (Summers, 1977; Biermann, 1978). In machine learning,probabilistic program induction has been used successfully in many settings, such as learning tosolve simple Q&A (Liang et al., 2010; Neelakantan et al., 2015; Andreas et al., 2016), sort a list ofnumbers (Reed & de Freitas, 2015), and learning with very few examples (Lake et al., 2015).
The controller in Neural Architecture Search is auto-regressive, which means it predicts hyperpa-rameters one a time, conditioned on previous predictions. This idea is borrowed from the decoderin end-to-end sequence to sequence learning (Sutskever et al., 2014). Unlike sequence to sequencelearning, our method optimizes a non-differentiable metric, which is the accuracy of the child net-work. It is therefore similar to the work on BLEU optimization in Neural Machine Translation (Ran-zato et al., 2015; Shen et al., 2016). Unlike these approaches, our method learns directly from thereward signal without any supervised bootstrapping.
Also related to our work is the idea of learning to learn or meta-learning (Thrun & Pratt, 2012), ageneral framework of using information learned in one task to improve a future task. More closelyrelated is the idea of using a neural network to learn the gradient descent updates for another net-work (Andrychowicz et al., 2016) and the idea of using reinforcement learning to find update policiesfor another network (Li & Malik, 2016).
神经架构搜索与程序合成和归纳编程有一些相似之处,它们从例子中搜索程序(Summers,1977; Biermann,1978)。在机器学习中,概率性程序诱导已成功用于许多环境中,比如学习简单问答(Liang et al。,2010; Neelakantan et al。,2015; Andreas et al。,2016),对数字列表(Reed &de Freitas,2015年),并以极少数例子进行学习(Lake等,2015)。
神经架构搜索中的控制器是自动回归的,这意味着它预测一次一次的超参数,并以先前的预测为条件。这个想法是从decoderin端对端序列借鉴序列学习(Sutskever等,2014)。与序列学习序列不同,我们的方法优化了一个不可区分的度量标准,这是子网络的准确性。因此它类似于神经机器翻译中的BLEU优化工作(Ran-zato等,2015; Shen等,2016)。与这些方法不同,我们的方法直接从没有任何监督引导的信号中学习。
与我们的工作相关的还有学习学习或元学习的想法(Thrun&Pratt,2012),这是一个使用在一项任务中学到的信息来改进未来任务的通用框架。更密切相关的是使用神经网络学习另一网络的梯度下降更新(Andrychowicz et al。,2016)以及使用强化学习为另一网络找到更新策略的想法(Li&Malik,2016)。
3 METHODS
In the following section, we will first describe a simple method of using a recurrent network togenerate convolutional architectures. We will show how the recurrent network can be trained witha policy gradient method to maximize the expected accuracy of the sampled architectures. We willpresent several improvements of our core approach such as forming skip connections to increasemodel complexity and using a parameter server approach to speed up training. In the last part of the section, we will focus on generating recurrent architectures, which is another key contribution of our paper.
3方法
在下一节中,我们将首先描述使用循环网络生成卷积体系结构的简单方法。 我们将展示如何使用策略梯度法来训练周期性网络,以最大化采样体系结构的预期准确度。 我们将对我们的核心方法进行若干改进,例如形成跳过连接以增加模型复杂性,并使用参数服务器方法加速培训。 在本节的最后部分,我们将重点介绍生成经常性架构,这是我们论文的另一个重要贡献。
3.1 GENERATE MODEL DESCRIPTIONS WITH A CONTROLLER RECURRENT NEURALNETWORK
In Neural Architecture Search, we use a controller to generate architectural hyperparameters ofneural networks. To be flexible, the controller is implemented as a recurrent neural network. Let’ssuppose we would like to predict feedforward neural networks with only convolutional layers, wecan use the controller to generate their hyperparameters as a sequence of tokens:
In our experiments, the process of generating an architecture stops if the number of layers exceedsa certain value. This value follows a schedule where we increase it as training progresses. Once thecontroller RNN finishes generating an architecture, a neural network with this architecture is builtand trained. At convergence, the accuracy of the network on a held-out validation set is recorded.The parameters of the controller RNN, θc, are then optimized in order to maximize the expectedvalidation accuracy of the proposed architectures. In the next section, we will describe a policygradient method which we use to update parameters θc so that the controller RNN generates betterarchitectures over time.
3.1用控制器递归神经网络生成模型描述
在神经架构搜索中,我们使用控制器来生成神经网络的架构超参数。为了灵活,控制器被实现为循环神经网络。假设我们想要预测只有卷积层的前向神经网络,我们可以使用控制器生成他们的超参数作为令牌序列:
在我们的实验中,如果层数超过一定值,生成架构的过程将停止。这个值遵循一个时间表,我们随着培训的进展而增加它。一旦控制器RNN完成生成架构,具有此架构的神经网络就建立起来并接受培训。在收敛时,网络在保留验证集上的准确性被记录下来。然后对控制器RNN,θc的参数进行优化,以使所提出的体系结构的预期验证准确度最大化。在下一节中,我们将描述一个策略梯度方法,我们用它来更新参数θc,以便控制器RNN随着时间的推移生成相应的建筑物。
3.2 TRAINING WITH REINFORCE
The list of tokens that the controller predicts can be viewed as a list of actions a1:T to design anarchitecture for a child network. At convergence, this child network will achieve an accuracy R ona held-out dataset. We can use this accuracy R as the reward signal and use reinforcement learningto train the controller. More concretely, to find the optimal architecture, we ask our controller tomaximize its expected reward, represented by J(θc): J(θc) = EP(a1:T ;θc)[R]
3.2加强训练
控制器预测的令牌列表可以被视为一系列动作a1:T来为子网络设计架构。 在收敛时,这个子网络将实现一个准确的数据集。 我们可以使用这个精度R作为奖励信号,并使用强化学习来训练控制器。 更具体地说,为了找到最佳的架构,我们要求我们的控制器最大化其期望的奖励,用J(θc)表示:J(θc) = EP(a1:T ;θc)[R]
Since the reward signal R is non-differentiable, we need to use a policy gradient method to iterativelyupdate θc. In this work, we use the REINFORCE rule from Williams (1992): 公式
An empirical approximation of the above quantity is: 公式
Where m is the number of different architectures that the controller samples in one batch and T is
the number of hyperparameters our controller has to predict to design a neural network architecture.3
The validation accuracy that the k-th neural network architecture achieves after being trained on atraining dataset is Rk.
The above update is an unbiased estimate for our gradient, but has a very high variance. In order toreduce the variance of this estimate we employ a baseline function:公式,
As long as the baseline function b does not depend on the on the current action, then this is still anunbiased gradient estimate. In this work, our baseline b is an exponential moving average of theprevious architecture accuracies.
由于回报信号R是不可微分的,因此我们需要使用策略梯度方法迭代更新θc。 在这项工作中,我们使用Williams(1992)的REINFORCE规则:公式
上述数量的经验近似值为:公式
其中m是控制器在一个批次中采样并且T是不同架构的数量
我们的控制器必须预测设计神经网络体系结构的超参数的数量
第k个神经网络体系结构在训练数据集之后达到的验证准确度为Rk。
以上更新是我们渐变的无偏估计,但具有非常高的方差。 为了减少这个估计的方差,我们使用了一个基线函数:公式,
只要基线函数b不依赖于当前动作,那么这仍然是有偏差的梯度估计。 在这项工作中,我们的基线b是以前架构精度的指数移动平均值。
Accelerate Training with Parallelism and Asynchronous Updates: In Neural ArchitectureSearch, each gradient update to the controller parameters θc corresponds to training one child net-work to convergence. As training a child network can take hours, we use distributed training andasynchronous parameter updates in order to speed up the learning process of the controller (Deanet al., 2012). We use a parameter-server scheme where we have a parameter server of S shards, thatstore the shared parameters for K controller replicas. Each controller replica samples m differentchild architectures that are trained in parallel. The controller then collects gradients according to theresults of that minibatch of m architectures at convergence and sends them to the parameter serverin order to update the weights across all controller replicas. In our implementation, convergence ofeach child network is reached when its training exceeds a certain number of epochs. This scheme ofparallelism is summarized in Figure 3.
通过并行和异步更新加速训练:在Neural ArchitectureSearch中,控制器参数θc的每个梯度更新对应于训练一个孩子网络收敛。由于训练子网络可能需要数小时,我们使用分布式培训和同步参数更新以加速控制器的学习过程(Dean等,2012)。我们使用参数服务器方案,其中有一个S分片的参数服务器,它存储K控制器副本的共享参数。每个控制器副本采样m个并行训练的不同的儿童架构。然后,控制器根据收敛的m个体系结构的小批次的结果收集梯度,并将它们发送到参数服务器以更新所有控制器副本中的权重。在我们的实施中,当其训练超过一定数量的时期时,达到每个儿童网络的融合。图3总结了这种并行性方案。
3.3 INCREASE ARCHITECTURE COMPLEXITY WITH SKIP CONNECTIONS AND OTHERLAYER TYPES
In Section 3.1, the search space does not have skip connections, or branching layers used in modernarchitectures such as GoogleNet (Szegedy et al., 2015), and Residual Net (He et al., 2016a). In thissection we introduce a method that allows our controller to propose skip connections or branchinglayers, thereby widening the search space.
To enable the controller to predict such connections, we use a set-selection type attention (Neelakan-tan et al., 2015) which was built upon the attention mechanism (Bahdanau et al., 2015; Vinyals et al.,2015). At layer N , we add an anchor point which has N − 1 content-based sigmoids to indicate theprevious layers that need to be connected. Each sigmoid is a function of the current hiddenstate ofthe controller and the previous hiddenstates of the previous N − 1 anchor points:
P(Layer j is an input to layer i) = sigmoid(vTtanh(Wprev ∗ hj + Wcurr ∗ hi)),
3.3增加跳过连接和其他层类型的体系结构复杂性
在3.1节中,搜索空间没有跳过连接,或者在GoogleNet(Szegedy et al。,2015)和Residual Net(He et al。,2016a)等现代架构中使用的分支层。 在本节中,我们介绍一种方法,允许我们的控制器提出跳过连接或分支层,从而拓宽搜索空间。
为了使控制器能够预测这种联系,我们使用了基于注意机制(Bahdanau等,2015; Vinyals等,2015)的集合选择型关注(Neelakan-tan等,2015)。 在第N层,我们添加一个锚点,它具有N - 1个基于内容的S形指示,以指示需要连接的以前的图层。 每个S形是控制器的当前隐藏状态和先前N-1个锚点的先前隐藏状态的函数:P(Layer j is an input to layer i) = sigmoid(vTtanh(Wprev ∗ hj + Wcurr ∗ hi)),
where hj represents the hiddenstate of the controller at anchor point for the j-th layer, where jranges from 0 to N − 1. We then sample from these sigmoids to decide what previous layers to beused as inputs to the current layer. The matrices Wprev, Wcurr and v are trainable parameters. As these connections are also defined by probability distributions, the REINFORCE method still applies without any significant modifications. Figure 4 shows how the controller uses skip connections to decide what layers it wants as inputs to the current layer.
In our framework, if one layer has many input layers then all input layers are concatenated in thedepth dimension. Skip connections can cause “compilation failures” where one layer is not compat-ible with another layer, or one layer may not have any input or output. To circumvent these issues,we employ three simple techniques. First, if a layer is not connected to any input layer then theimage is used as the input layer. Second, at the final layer we take all layer outputs that have notbeen connected and concatenate them before sending this final hiddenstate to the classifier. Lastly,if input layers to be concatenated have different sizes, we pad the small layers with zeros so that theconcatenated layers have the same sizes.
Finally, in Section 3.1, we do not predict the learning rate and we also assume that the architecturesconsist of only convolutional layers, which is also quite restrictive. It is possible to add the learningrate as one of the predictions. Additionally, it is also possible to predict pooling, local contrastnormalization (Jarrett et al., 2009; Krizhevsky et al., 2012), and batchnorm (Ioffe & Szegedy, 2015)in the architectures. To be able to add more types of layers, we need to add an additional step in thecontroller RNN to predict the layer type, then other hyperparameters associated with it.
其中hj表示控制器在第j层的锚点处的隐藏状态,其中从0到N-1的范围从0到N-1。然后,我们从这些乙状结构中采样以确定先前哪些层被用作当前层的输入。矩阵Wprev,Wcurr和v是可训练参数。由于这些连接也是由概率分布定义的,REINFORCE方法仍然适用,没有任何重大修改。图4显示了控制器如何使用跳转连接来决定它想要的层作为当前层的输入。
在我们的框架中,如果一个图层具有多个输入图层,则所有输入图层都将在深度维度中连接起来。跳过连接会导致“编译失败”,其中一个图层与另一图层不兼容,或者一个图层可能没有任何输入或输出。为了规避这些问题,我们采用了三种简单的技术。首先,如果图层没有连接到任何输入图层,则图像将被用作输入图层。其次,在最后一层,我们将所有未连接的图层输出连接起来,并将它们连接起来,然后将最终的隐藏状态发送给分类器。最后,如果要连接的输入图层具有不同的大小,我们使用零填充小图层,以便相关图层具有相同的大小。
最后,在第3.1节中,我们不预测学习速率,并且我们还假定架构仅包含卷积层,这也是非常严格的。可以将学习速率添加为预测之一。此外,还可以在体系结构中预测汇集,局部对比度归一化(Jarrett等人,2009; Krizhevsky等人,2012)和蝙蝠技术(Ioffe&Szegedy,2015)。为了能够添加更多类型的图层,我们需要在控制器RNN中添加一个额外的步骤来预测图层类型,然后预测与其关联的其他超参数。
3.4 GENERATE RECURRENT CELL ARCHITECTURES
In this section, we will modify the above method to generate recurrent cells. At every time step t,the controller needs to find a functional form for ht that takes xt and ht−1 as inputs. The simplestway is to have ht = tanh(W1 ∗xt +W2 ∗ht−1), which is the formulation of a basic recurrent cell. Amore complicated formulation is the widely-used LSTM recurrent cell (Hochreiter & Schmidhuber,1997).
3.4生成回归的细胞结构
在本节中,我们将修改上述方法以生成循环单元格。 在每一步t,控制器都需要找到一个以xt和ht-1为输入的ht的函数形式。 最简单的方法是让ht = tanh(W1 * xt + W2 * ht-1),这是基本复发单元格的表达式。 Amore复杂的配方是广泛使用的LSTM复发细胞(Hochreiter&Schmidhuber,1997)。
The computations for basic RNN and LSTM cells can be generalized as a tree of steps that take xtand ht−1 as inputs and produce ht as final output. The controller RNN needs to label each node inthe tree with a combination method (addition, elementwise multiplication, etc.) and an activationfunction (tanh, sigmoid, etc.) to merge two inputs and produce one output. Two outputs are thenfed as inputs to the next node in the tree. To allow the controller RNN to select these methods andfunctions, we index the nodes in the tree in an order so that the controller RNN can visit each nodeone by one and label the needed hyperparameters.
Inspired by the construction of the LSTM cell (Hochreiter & Schmidhuber, 1997), we also need cellvariables ct−1 and ct to represent the memory states. To incorporate these variables, we need thecontroller RNN to predict what nodes in the tree to connect these two variables to. These predictionscan be done in the last two blocks of the controller RNN.
基本RNN和LSTM单元的计算可以概括为以xtand ht-1作为输入并产生ht作为最终输出的步骤树。 控制器RNN需要用组合方法(加法,元素乘法等)和激活函数(tanh,sigmoid等)来标记树中的每个节点以合并两个输入并产生一个输出。 然后两个输出作为树中下一个节点的输入。 为了允许控制器RNN选择这些方法和功能,我们按照顺序对树中的节点进行索引,使得控制器RNN可以访问每个节点,并标记所需的超参数。
受到LSTM细胞构建的启发(Hochreiter&Schmidhuber,1997),我们还需要细胞变量ct-1和ct来表示记忆状态。 为了结合这些变量,我们需要控制器RNN来预测树中将这两个变量连接到哪些节点。 这些预测可以在控制器RNN的最后两个块中完成。
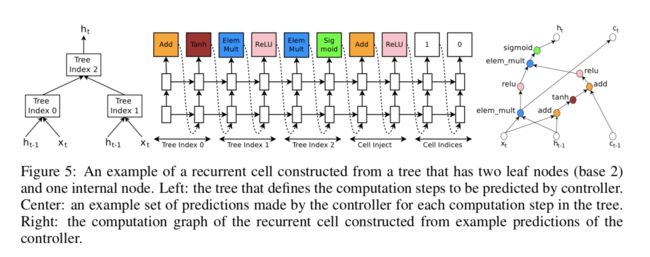
To make this process more clear, we show an example in Figure 5, for a tree structure that has twoleaf nodes and one internal node. The leaf nodes are indexed by 0 and 1, and the internal node isindexed by 2. The controller RNN needs to first predict 3 blocks, each block specifying a combina-tion method and an activation function for each tree index. After that it needs to predict the last 2blocks that specify how to connect ct and ct−1 to temporary variables inside the tree. Specifically,according to the predictions of the controller RNN in this example, the following computation steps will occur:
- The controller predicts Add and T anh for tree index 0, this means we need to computea0 = tanh(W1 ∗xt +W2 ∗ht−1).
- The controller predicts ElemMult and ReLU for tree index 1, this means we need tocompute a1 = ReLU (W3 ∗ xt) ⊙ (W4 ∗ ht−1) .
- The controller predicts 0 for the second element of the “Cell Index”, Add and ReLU forelements in “Cell Inject”, which means we need to compute anew = ReLU(a + c ).
0 0t−1Notice that we don’t have any learnable parameters for the internal nodes of the tree.
- The controller predicts ElemMult and Sigmoid for tree index 2, this means we need tocompute a = sigmoid(anew ⊙ a ). Since the maximum index in the tree is 2, h is set to201t a2.
- The controller RNN predicts 1 for the first element of the “Cell Index”, this means that weshould set ct to the output of the tree at index 1 before the activation, i.e., ct = (W3 ∗ xt ) ⊙(W4 ∗ ht−1).
In the above example, the tree has two leaf nodes, thus it is called a “base 2” architecture. In ourexperiments, we use a base number of 8 to make sure that the cell is expressive.
为了使这个过程更加清晰,我们在图5中显示了一个例子,其中包含两个节点和一个内部节点的树结构。 叶节点由0和1索引,内部节点索引为2.控制器RNN需要首先预测3个块,每个块指定每个树索引的组合方法和激活函数。 之后,它需要预测最后的2blocks,它指定如何将ct和ct-1连接到树内的临时变量。 具体而言,根据该示例中的控制器RNN的预测,将发生以下计算步骤:
- 控制器预测树索引0的Add和T anh,这意味着我们需要计算a0 = tanh(W1 * xt + W2 * ht-1)。
- 控制器预测树索引1的ElemMult和ReLU,这意味着我们需要计算a1 = ReLU(W3 * xt)⊙(W4 * ht-1)。
- 控制器对“细胞索引”的第二个元素,“细胞入射”中的Add和ReLU前缀预测0,这意味着我们需要计算新的= ReLU(a + c)。0 0t-1注意我们没有任何树的内部节点的可学习参数。
- 控制器预测树索引2的ElemMult和Sigmoid,这意味着我们需要计算一个= sigmoid(a new⊙a)。由于树中的最大索引是2,所以h被设置为
- 控制器RNN为“Cell索引”的第一个元素预测1,这意味着在激活之前,应该将ct设置为索引1处的树的输出,即ct =(W3 * xt)⊙(W4 * ht -1)。
在上面的例子中,树有两个叶子节点,因此它被称为“基础2”体系结构。在实验中,我们使用8的基数来确保细胞具有表达力。
4 EXPERIMENTS AND RESULTS
We apply our method to an image classification task with CIFAR-10 and a language modeling taskwith Penn Treebank, two of the most benchmarked datasets in deep learning. On CIFAR-10, ourgoal is to find a good convolutional architecture whereas on Penn Treebank our goal is to find a goodrecurrent cell. On each dataset, we have a separate held-out validation dataset to compute the rewardsignal. The reported performance on the test set is computed only once for the network that achievesthe best result on the held-out validation dataset. More details about our experimental proceduresand results are as follows.
4实验和结果
我们将该方法应用于CIFAR-10的图像分类任务和Penn Treebank的语言建模任务,这是深度学习中两个最基准的数据集。 在CIFAR-10上,我们的目标是找到一个良好的卷积体系结构,而在宾夕法尼亚州立大学我们的目标是找到一个良好的细胞。 在每个数据集上,我们都有一个单独的外部验证数据集来计算奖励信号。 所报告的测试集的性能仅对在持有验证数据集上获得最佳结果的网络计算一次。 关于我们的实验程序和结果的更多细节如下。
4.1 LEARNING CONVOLUTIONAL ARCHITECTURES FOR CIFAR-10
Dataset: In these experiments we use the CIFAR-10 dataset with data preprocessing and aug-mentation procedures that are in line with other previous results. We first preprocess the data bywhitening all the images. Additionally, we upsample each image then choose a random 32x32 cropof this upsampled image. Finally, we use random horizontal flips on this 32x32 cropped image.
Search space: Our search space consists of convolutional architectures, with rectified linear unitsas non-linearities (Nair & Hinton, 2010), batch normalization (Ioffe & Szegedy, 2015) and skipconnections between layers (Section 3.3). For every convolutional layer, the controller RNN has toselect a filter height in [1, 3, 5, 7], a filter width in [1, 3, 5, 7], and a number of filters in [24, 36, 48,64]. For strides, we perform two sets of experiments, one where we fix the strides to be 1, and onewhere we allow the controller to predict the strides in [1, 2, 3].
Training details: The controller RNN is a two-layer LSTM with 35 hidden units on each layer.It is trained with the ADAM optimizer (Kingma & Ba, 2015) with a learning rate of 0.0006. Theweights of the controller are initialized uniformly between -0.08 and 0.08. For the distributed train-ing, we set the number of parameter server shards S to 20, the number of controller replicas K to100 and the number of child replicas m to 8, which means there are 800 networks being trained on800 GPUs concurrently at any time.
Once the controller RNN samples an architecture, a child model is constructed and trained for 50epochs. The reward used for updating the controller is the maximum validation accuracy of the last5 epochs cubed. The validation set has 5,000 examples randomly sampled from the training set,the remaining 45,000 examples are used for training. The settings for training the CIFAR-10 childmodels are the same with those used in Huang et al. (2016a). We use the Momentum Optimizerwith a learning rate of 0.1, weight decay of 1e-4, momentum of 0.9 and used Nesterov Momentum(Sutskever et al., 2013).
4.1 CIFAR-10的学习型教学体系结构
数据集:在这些实验中,我们使用CIFAR-10数据集,其数据预处理和增强过程与其他先前的结果一致。 我们首先通过清理所有图像来预处理数据。 另外,我们对每幅图像进行上采样,然后选择上采样图像的随机32x32作物。 最后,我们在这个32x32裁剪图像上使用随机水平翻转。
搜索空间:我们的搜索空间由卷积体系结构组成,其整体线性单位为非线性(Nair&Hinton,2010),批量归一化(Ioffe&Szegedy,2015)以及层间跳过连接(第3.3节)。对于每个卷积层,控制器RNN选择[1,3,5,7]中的滤波器高度,[1,3,5,7]中的滤波器宽度和[24,36,48中的滤波器数量,64]。对于步幅,我们执行两组实验,其中我们将步幅固定为1,另一个位置我们允许控制器预测[1,2,3]中的步幅。
训练细节:控制器RNN是一个两层LSTM,每层有35个隐藏单元。它使用ADAM优化器(Kingma&Ba,2015)进行训练,学习率为0.0006。控制器的重量在-0.08和0.08之间均匀初始化。对于分布式训练,我们将参数服务器分片数S设置为20,控制器副本数K为100,子副本数m为8,这意味着在任何时候800个GPU同时训练了800个网络。
一旦控制器RNN对架构进行采样,就构建并训练了50个子模型的子模型。用于更新控制器的奖励是最后5个时期立方体的最大验证准确性。验证集有5000个从训练集中随机抽样的例子,其余45,000个例子用于训练。培训CIFAR-10儿童模型的设置与Huang等人使用的相同。 (2016a)。我们使用Momentum Optimizer,学习率为0.1,体重衰减为1e-4,动量为0.9,并使用Nesterov Momentum(Sutskever et al。,2013)。
During the training of the controller, we use a schedule of increasing number of layers in the childnetworks as training progresses. On CIFAR-10, we ask the controller to increase the depth by 2 forthe child models every 1,600 samples, starting at 6 layers.
Results: After the controller trains 12,800 architectures, we find the architecture that achieves thebest validation accuracy. We then run a small grid search over learning rate, weight decay, batchnormepsilon and what epoch to decay the learning rate. The best model from this grid search is then rununtil convergence and we then compute the test accuracy of such model and summarize the resultsin Table 1. As can be seen from the table, Neural Architecture Search can design several promisingarchitectures that perform as well as some of the best models on this dataset.
在对控制器进行培训期间,随着培训的进展,我们使用一个日益增加的子网络层数的时间表。 在CIFAR-10上,我们要求控制器从6层开始,每1,600个样本增加2个子模型的深度。
结果:控制器训练了12,800个体系结构后,我们发现达到最佳验证准确性的体系结构。 然后,我们对学习速率,体重衰减,batchnormepsilon以及衰减学习速率的时间进行小网格搜索。 然后,这个网格搜索的最佳模型运行收敛,然后我们计算这种模型的测试精度并总结表1中的结果。从表中可以看出,神经架构搜索可以设计几个有前景的体系结构,其性能和部分 这个数据集上的最佳模型。
First, if we ask the controller to not predict stride or pooling, it can design a 15-layer architecture that achieves 5.50% error rate on the test set. This architecture has a good balance between accuracy and depth. In fact, it is the shallowest and perhaps the most inexpensive architecture among the top performing networks in this table. This architecture is shown in Appendix A, Figure 7. A notable feature of this architecture is that it has many rectangular filters and it prefers larger filters at the top layers. Like residual networks (He et al., 2016a), the architecture also has many one-step skip connections. This architecture is a local optimum in the sense that if we perturb it, its performance becomes worse. For example, if we densely connect all layers with skip connections, its performance becomes slightly worse: 5.56%. If we remove all skip connections, its performance drops to 7.97%.
In the second set of experiments, we ask the controller to predict strides in addition to other hyper-parameters. As stated earlier, this is more challenging because the search space is larger. In thiscase, it finds a 20-layer architecture that achieves 6.01% error rate on the test set, which is not muchworse than the first set of experiments.
Finally, if we allow the controller to include 2 pooling layers at layer 13 and layer 24 of the archi-tectures, the controller can design a 39-layer network that achieves 4.47% which is very close tothe best human-invented architecture that achieves 3.74%. To limit the search space complexity wehave our model predict 13 layers where each layer prediction is a fully connected block of 3 layers.Additionally, we change the number of filters our model can predict from [24, 36, 48, 64] to [6, 12,24, 36]. Our result can be improved to 3.65% by adding 40 more filters to each layer of our archi-tecture. Additionally this model with 40 filters added is 1.05x as fast as the DenseNet model thatachieves 3.74%, while having better performance. The DenseNet model that achieves 3.46% errorrate (Huang et al., 2016b) uses 1x1 convolutions to reduce its total number of parameters, which wedid not do, so it is not an exact comparison.
首先,如果我们要求控制器不预测跨度或池,它可以设计一个15层架构,在测试集上可以达到5.50%的错误率。这种架构在精度和深度之间具有良好的平衡。事实上,它是本表中表现最佳的网络中最浅的,也许是最便宜的架构。该体系结构如附录A,图7所示。该体系结构的一个显着特点是它具有许多矩形滤波器,并且它在顶层更喜欢较大的滤波器。像残差网络一样(He et al。,2016a),该架构还有许多一步跳过连接。这种架构是一种局部最优的,因为如果我们扰乱它,它的性能就会变差。例如,如果我们用跳跃连接密集连接所有层,则其性能会变得稍差:5.56%。如果我们删除所有跳过连接,它的性能下降到7.97%。
在第二组实验中,除了其他超参数之外,我们还要求控制器预测步幅。如前所述,这是更具挑战性的,因为搜索空间更大。在这种情况下,它找到了一个20层体系结构,在测试集上可以达到6.01%的错误率,这比第一组实验没有什么大不了。
最后,如果我们允许控制器在架构的第13层和第24层包含2个汇聚层,控制器可以设计一个39层网络,达到4.47%,这非常接近最佳人造架构,达到3.74 %。为了限制搜索空间的复杂性,我们的模型预测了13层,其中每层预测是3层完全连接的块。此外,我们将模型可以预测的滤波器数量从[24,36,48,64]改变为[6 ,12,24,36]。我们的结果可以通过在我们的架构的每一层增加40个更多的过滤器而提高到3.65%。此外,这款机型增加了40个过滤器,其速度是DenseNet模型的1.05倍,达到3.74%,同时具有更好的性能。达到3.46%误差率的DenseNet模型(Huang等人,2016b)使用1x1卷积来减少其参数的总数量,这是无法完成的,所以它不是一个确切的比较。
4.2 LEARNING RECURRENT CELLS FOR PENN TREEBANK
Dataset: We apply Neural Architecture Search to the Penn Treebank dataset, a well-known bench-mark for language modeling. On this task, LSTM architectures tend to excel (Zaremba et al., 2014;Gal, 2015), and improving them is difficult (Jozefowicz et al., 2015). As PTB is a small dataset, reg-ularization methods are needed to avoid overfitting. First, we make use of the embedding dropoutand recurrent dropout techniques proposed in Zaremba et al. (2014) and (Gal, 2015). We also try tocombine them with the method of sharing Input and Output embeddings, e.g., Bengio et al. (2003);Mnih & Hinton (2007), especially Inan et al. (2016) and Press & Wolf (2016). Results with thismethod are marked with “shared embeddings.”
Search space: Following Section 3.4, our controller sequentially predicts a combination methodthen an activation function for each node in the tree. For each node in the tree, the controllerRNN needs to select a combination method in [add, elem mult] and an activation method in[identity,tanh,sigmoid,relu]. The number of input pairs to the RNN cell is called the “basenumber” and set to 8 in our experiments. When the base number is 8, the search space is has ap-proximately 6 × 1016 architectures, which is much larger than 15,000, the number of architecturesthat we allow our controller to evaluate.
4.2为PENN TREEBANK学习循环细胞
数据集:我们将神经架构搜索应用于Penn Treebank数据集,这是一个众所周知的语言建模基准。在这项任务中,LSTM架构倾向于优秀(Zaremba等,2014; Gal,2015),并且改进它们是困难的(Jozefowicz等,2015)。由于PTB是一个小型数据集,因此需要使用reg-ularization方法来避免过度拟合。首先,我们利用Zaremba等人提出的嵌入丢失和回归丢失技术。 (2014年)和(Gal,2015年)。我们也尝试将它们与共享输入和输出嵌入的方法结合起来,例如Bengio等人。 (2003); Mnih&Hinton(2007),特别是Inan等人(2016)和Press&Wolf(2016)。此方法的结果标记为“共享嵌入”。
搜索空间:在3.4节之后,我们的控制器顺序地预测一个组合方法,然后是树中每个节点的激活函数。对于树中的每个节点,controllerRNN需要在[add,elem mult]中选择一种组合方法,并在[identity,tanh,sigmoid,relu]中选择一种激活方法。 RNN小区的输入对数目称为“基数”,在我们的实验中设为8。当基数为8时,搜索空间大约有6×1016个体系结构,这比我们允许控制器评估的体系结构的数量大得多。
Training details: The controller and its training are almost identical to the CIFAR-10 experimentsexcept for a few modifications: 1) the learning rate for the controller RNN is 0.0005, slightly smallerthan that of the controller RNN in CIFAR-10, 2) in the distributed training, we set S to 20, K to 400and m to 1, which means there are 400 networks being trained on 400 CPUs concurrently at anytime, 3) during asynchronous training we only do parameter updates to the parameter-server once10 gradients from replicas have been accumulated.
In our experiments, every child model is constructed and trained for 35 epochs. Every child modelhas two layers, with the number of hidden units adjusted so that total number of learnable parametersapproximately match the “medium” baselines (Zaremba et al., 2014; Gal, 2015). In these experi-ments we only have the controller predict the RNN cell structure and fix all other hyperparameters.The reward function is c where c is a constant, usually set at 80.
After the controller RNN is done training, we take the best RNN cell according to the lowest validation perplexity and then run a grid search over learning rate, weight initialization, dropout rates and decay epoch. The best cell found was then run with three different configurations and sizes to increase its capacity.
训练细节:控制器及其培训与CIFAR-10实验几乎相同,只是进行了一些修改:1)控制器RNN的学习率为0.0005,略低于CIFAR-10中控制器RNN的学习率; 2)分布式培训,我们将S设置为20,K设为400,m设为1,这意味着400个网络随时都在400个CPU上同时进行培训,3)在异步培训期间,我们只对参数服务器进行一次参数更新,已经积累了。
在我们的实验中,每个儿童模型都经过了35个时期的构建和训练。每个儿童模型都有两层,调整隐藏单元的数量,以使可学习参数的总数大致与“中等”基线相匹配(Zaremba等,2014; Gal,2015)。在这些实验中,我们只有控制器预测RNN单元结构并修复所有其他超参数。奖励函数是c,其中c是常数,通常设为80。
在控制器RNN完成训练后,我们根据最低验证困惑度选取最佳RNN小区,然后对学习速率,权重初始化,丢失率和衰减时期进行网格搜索。然后找到最好的细胞,然后用三种不同的配置和尺寸运行以增加其容量。
Results: In Table 2, we provide a comprehensive list of architectures and their performance onthe PTB dataset. As can be seen from the table, the models found by Neural Architecture Searchoutperform other state-of-the-art models on this dataset, and one of our best models achieves a gainof almost 3.6 perplexity. Not only is our cell is better, the model that achieves 64 perplexity is alsomore than two times faster because the previous best network requires running a cell 10 times pertime step (Zilly et al., 2016).
The newly discovered cell is visualized in Figure 8 in Appendix A. The visualization reveals thatthe new cell has many similarities to the LSTM cell in the first few steps, such as it likes to computeW1 ∗ ht−1 + W2 ∗ xt several times and send them to different components in the cell.
Transfer Learning Results: To understand whether the cell can generalize to a different task, weapply it to the character language modeling task on the same dataset. We use an experimental setupthat is similar to Ha et al. (2016), but use variational dropout by Gal (2015). We also train our ownLSTM with our setup to get a fair LSTM baseline. Models are trained for 80K steps and the best testset perplexity is taken according to the step where validation set perplexity is the best. The resultson the test set of our method and state-of-art methods are reported in Table 3. The results on smallsettings with 5-6M parameters confirm that the new cell does indeed generalize, and is better thanthe LSTM cell.
结果:在表2中,我们提供了关于PTB数据集的体系结构及其性能的完整列表。从表中可以看出,Neural Architecture Search找到的模型可以在这个数据集上实现其他最先进的模型,而我们最好的模型之一可以获得接近3.6的困惑。我们的细胞不仅更好,而且实现64次困惑的模型比现在快两倍,因为之前最好的网络需要运行10次细胞步骤(Zilly等,2016)。
新发现的细胞在图8中附录A中的可视化显示thatthe新的细胞有许多相似之处LSTM细胞中的前几个步骤,比如它喜欢computeW1 * HT-1 + W2 * XT几次,送可视化他们对细胞中的不同组分。
迁移学习结果:为了理解单元格是否可以推广到不同的任务,我们将它应用到同一数据集上的角色语言建模任务。我们使用与Ha等人相似的实验设置。 (2016),但使用Gal(2015)的变差辍学率。我们还通过我们的设置培训我们自己的LSTM以获得公平的LSTM基准。模型经过80K步骤的训练,根据验证集合困惑度最好的步骤,采用最好的测试集困惑度。表3中报告了我们的方法和现有技术方法的测试集的结果。具有5-6M参数的小型化的结果证实,新细胞确实是泛化的,并且比LSTM细胞更好。
Additionally, we carry out a larger experiment where the model has 16.28M parameters. This modelhas a weight decay rate of 1e − 4, was trained for 600K steps (longer than the above models) andthe test perplexity is taken where the validation set perplexity is highest. We use dropout rates of 0.2and 0.5 as described in Gal (2015), but do not use embedding dropout. We use the ADAM optimizerwith a learning rate of 0.001 and an input embedding size of 128. Our model had two layers with800 hidden units. We used a minibatch size of 32 and BPTT length of 100. With this setting, ourmodel achieves 1.214 perplexity, which is the new state-of-the-art result on this task.
Finally, we also drop our cell into the GNMT framework (Wu et al., 2016), which was previouslytuned for LSTM cells, and train an WMT14 English → German translation model. The GNMT network has 8 layers in the encoder, 8 layers in the decoder. The first layer of the encoder hasbidirectional connections. The attention module is a neural network with 1 hidden layer. When aLSTM cell is used, the number of hidden units in each layer is 1024. The model is trained in adistributed setting with a parameter sever and 12 workers. Additionally, each worker uses 8 GPUsand a minibatch of 128. We use Adam with a learning rate of 0.0002 in the first 60K training steps,and SGD with a learning rate of 0.5 until 400K steps. After that the learning rate is annealed bydividing by 2 after every 100K steps until it reaches 0.1. Training is stopped at 800K steps. Moredetails can be found in Wu et al. (2016).
另外,我们在模型有16.28M参数的情况下进行更大的实验。该模型的权重衰减率为1e-4,训练了600k步(比上述模型长),并且在验证集合困惑度最高时采用测试困惑度。如Gal(2015)所述,我们使用0.2和0.5的丢失率,但不使用嵌入丢失。我们使用ADAM优化器,学习率为0.001,输入嵌入大小为128.我们的模型有两层,包含800个隐藏单元。我们使用了32的minibatch大小和100的BPTT长度。通过这个设置,我们的模型达到了1.214的困惑度,这是该任务中最新的最新结果。
最后,我们也将我们的细胞放入GNMT框架(Wu et al。,2016),这个框架以前是用于LSTM细胞的,并培训WMT14英语→德语翻译模型。 GNMT网络在编码器中有8层,在解码器中有8层。编码器的第一层具有双向连接。注意模块是具有1个隐藏层的神经网络。当使用LSTM单元时,每层中隐藏单元的数量为1024.该模型通过参数服务器和12名工人在分布式设置中训练。此外,每位工作人员使用8个GPU和128个小批次。我们在前60,000个培训步骤中使用Adam的学习率为0.0002,SGD学习率为0.5,直到40万步。之后,每100K步骤将学习速率退化为2,直至达到0.1。训练停在800K步。更多细节可以在吴等人中找到。 (2016)。
In our experiment with the new cell, we make no change to the above settings except for dropping inthe new cell and adjusting the hyperparameters so that the new model should have the same compu-tational complexity with the base model. The result shows that our cell, with the same computationalcomplexity, achieves an improvement of 0.5 test set BLEU than the default LSTM cell. Though thisimprovement is not huge, the fact that the new cell can be used without any tuning on the existingGNMT framework is encouraging. We expect further tuning can help our cell perform better.
在我们对新单元的实验中,除了丢弃新单元和调整超参数以外,我们不改变上述设置,以便新模型与基本模型具有相同的计算复杂性。 结果表明,我们的单元具有相同的计算复杂性,比默认的LSTM单元实现了0.5个测试集BLEU的改进。 虽然这个改进并不是很大,但是新的单元可以在现有的GNMT框架中不用调整就可以使用,这是令人鼓舞的。 我们预计进一步调整可以帮助我们的电池表现更好。
Control Experiment 1 – Adding more functions in the search space: To test the robustness ofNeural Architecture Search, we add max to the list of combination functions and sin to the listof activation functions and rerun our experiments. The results show that even with a bigger searchspace, the model can achieve somewhat comparable performance. The best architecture with maxand sin is shown in Figure 8 in Appendix A.
Control Experiment 2 – Comparison against Random Search: Instead of policy gradient, onecan use random search to find the best network. Although this baseline seems simple, it is often veryhard to surpass (Bergstra & Bengio, 2012). We report the perplexity improvements using policygradient against random search as training progresses in Figure 6. The results show that not onlythe best model using policy gradient is better than the best model using random search, but also theaverage of top models is also much better.
控制实验1 - 在搜索空间中添加更多功能:为了测试神经架构搜索的鲁棒性,我们将max函数添加到激活函数列表的组合函数列表中,并重新运行我们的实验。 结果显示,即使有更大的搜索空间,该模型也可以达到一定的可比性能。 maxand sin的最佳架构如附录A中的图8所示。
控制实验2 - 与随机搜索的比较:可以使用随机搜索来找到最佳网络,而不是策略梯度。 虽然这个基线看起来很简单,但通常很难超越(Bergstra&Bengio,2012)。 在图6中,我们报告了随机搜索使用策略升级的困惑性改进情况。结果表明,不仅使用策略梯度的最佳模型优于使用随机搜索的最佳模型,而且顶级模型的平均值也更好。
5 CONCLUSION
In this paper we introduce Neural Architecture Search, an idea of using a recurrent neural network tocompose neural network architectures. By using recurrent network as the controller, our method isflexible so that it can search variable-length architecture space. Our method has strong empirical per-formance on very challenging benchmarks and presents a new research direction for automaticallyfinding good neural network architectures. The code for running the models found by the controlleron CIFAR-10 and PTB will be released at https://github.com/tensorflow/models . Additionally, wehave added the RNN cell found using our method under the name NASCell into TensorFlow, soothers can easily use it.
ACKNOWLEDGMENTS
We thank Greg Corrado, Jeff Dean, David Ha, Lukasz Kaiser and the Google Brain team for theirhelp with the project.
5结论
在本文中,我们介绍神经架构搜索,一种使用递归神经网络来构成神经网络架构的想法。 通过使用循环网络作为控制器,我们的方法是灵活的,因此它可以搜索可变长度的架构空间。 我们的方法在非常具有挑战性的基准上具有很强的经验性能,并为自动寻找良好的神经网络架构提供了一个新的研究方向。 在CIFAR-10和PTB上运行控制器发现的模型的代码将在https://github.com/tensorflow/models上发布。 此外,我们还将使用我们的方法发现的名为NASCell的RNN细胞添加到TensorFlow中,奶嘴可以轻松使用它。
致谢
我们感谢Greg Corrado,Jeff Dean,David Ha,Lukasz Kaiser和Google Brain团队为他们提供的帮助。
参考:https://blog.csdn.net/xjz18298268521/article/details/79078835