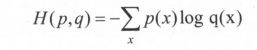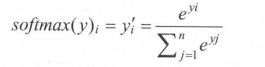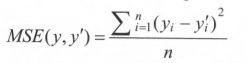【TensorFlow】TensorFlow从浅入深系列之六 -- 教你深入理解经典损失函数（交叉熵、均方误差）
本文是《TensorFlow从浅入深》系列之第6篇
TensorFlow从浅入深系列之一 -- 教你如何设置学习率（指数衰减法）
TensorFlow从浅入深系列之二 -- 教你通过思维导图深度理解深层神经网络
TensorFlow从浅入深系列之三 -- 教你如何对MNIST手写识别
TensorFlow从浅入深系列之四 -- 教你深入理解过拟合问题（正则化）
TensorFlow从浅入深系列之五 -- 教你详解滑动平均模型
目录
1、交叉熵
2、均方误差
1、交叉熵
交叉熵是分类问题中使用比较广的一种损失函数，刻画了两个概率分布之间的距离。
给定两个概率分布p和q，通过q来表示p的交叉熵为：
交叉熵刻画的是两个概率分布之间的距离，然而神经网络的输出却不一定是一个概率分布。Softmax回归就是一个非常常用的方法，用来将神经网络前向传播得到的结果变成概率分布。
交叉熵刻画的是通过概率分布q来表达概率分布p的困难程度。因为正确答案是希望得到的结果，所以当交叉熵作为神经网络的损失函数时，p代表的是正确答案，q代表的是预测值。交叉熵刻画的是两个概率分布的距离，也就是说交叉熵值越小， 两个概率分布越接近。
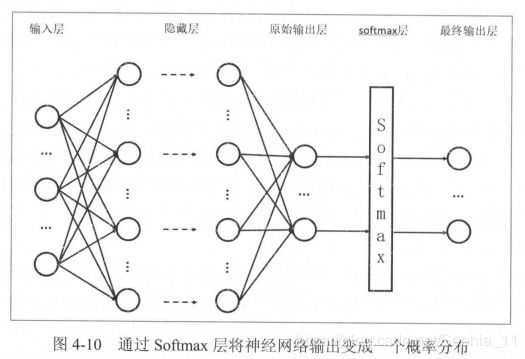
图4-10展示了加上Softmax回归的神经网络结构图。
假设原始的神经网络输出为
，
，…，
，那么经过Sotmax回归处理之后的输出为：
假设有一个分类问题，某个样例的正确答案是（1,0,0）。某模型经过Softmax回归之后的预测答案是（0.5,0.4,0.1），那么这个预测和正确答案之间的交叉熵为：
如果另外一个模型的预测是（0.8,0.1 ,0.1），那么这个预测值和真实值之间的交叉娟是：
从直观上可以很容易地知道第二个预测答案要优于第一个 。
TensorFlow实现交叉熵代码：
cross_entyopy=-tf.reduce_mean(y_*tf.log(tf.clip_by_balue(y,1e-10,1.0)))其中y_代表正确结果，y代表预测结果。（有对tf.clip_by_value函数不懂的，请参考本博客对其的介绍TensorFlow函数之tf.clip_by_value()）
因为交叉煽一般会与softmax回归一起使用，所以TensorFlow对这两个功能进行了统一封装，并提供了tf.nn.softmax_cross_entropy_with_logits函数。
Softmax回归之后的交叉熵损失函数：
cross_entropy = tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y )其中y代表了原始神经网络的输出结果，而 y_给出了标准答案 。
在只有一个正确答案的分类问题中，TensorFlow提供了tf.nn.sparse_softmax_cross_entropy_with_logits函数来进一步加速计算过程。（博客《TensorFlow：实战Google深度学习框架》--5.2.1 MNIST手写识别问题（程序已改进）有此方法的详细案例。）
2、均方误差
与分类问题不同，回归问题解决的是对具体数值的预测。比如房价预测、销量预测等都是回归问题。这些问题需要预测的不是一个事先定义好的类别，而是一个任意实数。解决回归问题的神经网络一般只有一个输出节点，这个节点的输出值就是预测值。
对于回归问题，最常用的损失函数是均方误差（MSE，mean squared error）。定义如下：
其中
为一个batch中第i个数据的正确答案，而
为神经网络给出的预测值。
TensorFlow实现均方误差函数：
mse=tf.reduce_mean(tf.square(y_-y))其中y代表了神经网络的输出答案,y_代表了标准答案 。