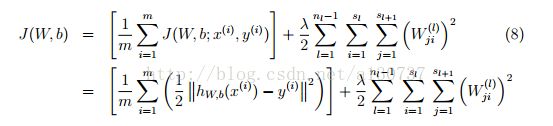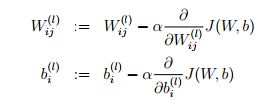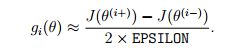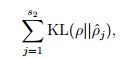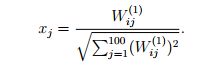sparse autoencoder(稀疏自动编码机)

预备知识（关于神经网络的）

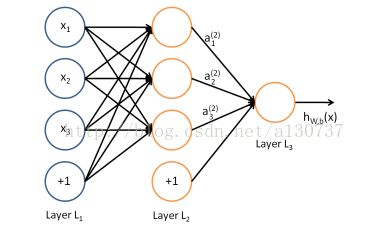
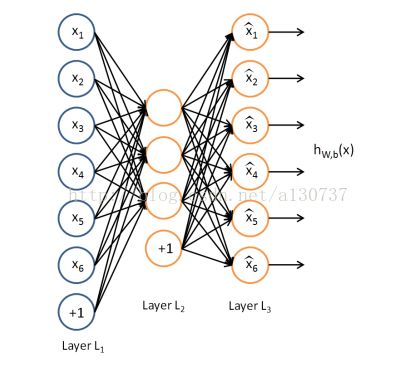
例如如下简单的网络：

模型参数 {W, b}， 

每个神经元是一个计算单元， 可以是hybolic tangent, 可以是sigmoid，也可以是rectifier linear， 等等。 现在大部分使用的是rectifier linear, 因为得到的performance 更好。

训练样本集可以是：

， m 个training examples

然后提出loss function(cost function)， 对于一个样本我们记为如下：

当时对于batch（注意不是mini batch, minibatch 每次只用样本集的一部分）， 全部样本的平均loss 使我们的training criterion:

、

为了避免过拟合， 我们对权重进行了L2 normalization（又称weight decay）， 注意没有对bias 进行regularizarion.

lamda 控制着 上述两项的相对权重。

上述的loss function 常常用于 classification 和 regression 的问题。 例如， 对于classification, y = 1 or 0 表示两个labels， recall that sigmoid function outputs values in 

[0, 1]， 如果使用tanh函数， 输出介于-1 和 1 之间， 我们也可以使用 -1 和 1 表示这两类. 

对于 regression的问题, 我们首先将我们的ouput scale 到 [0, 1]之间， 或者当使用tanh 函数的时候， scale 到 [-1, 1]之间。

我们的目的就是找到 W, b， 使得我们的J 最小化。为了训练我们的网络， 我们的第一步就是对网络的参数进行初始化。 初始化也是需要注意的， 不能随便初始化。 须知 training neural network is much like an art。 想想J是一个nonconvex 的函数， 也就是具有很多的local minimal， hinton 的那篇采用unsupervised greedy pretrain的办法就是得到了网络的更好的初始化的那一组参数， 使得我们能够得到更好的收敛效果， 至少不必最优点差多少。

note: 初始化W, b 到near 0 的随机值。 例如我们通过采样, ， 然后使用batch gradient descent 进行最小化J 得到相关的参数。

随机初始化的作用就是symmetry breaking, 如果所有参数军均初始化同一值， 我们最终学习到的所有参数值都是相同的了。

一次的参数更新公式如下：

总体来说， 我们使用的BP算法进行学习。  BP 算法是backward propagation errors 的简称。  BP 算法 常被considered to be a supervised learning method， 尽管BP 也常用于一些unsupervised networks such as autoencoder的训练。

BP 算法的伪代码如下：

我们可以利用matrix-vectorial notation 重新编写上述算法， 其中黑点代表element-wise product, 又称为 hadmard product。 matlab 中符号是 .*。

Implementation note:

上述的算法（2）， （3）步骤中， 我们需要计算： 对于所有的i, 

假设我们使用的是sigmoid activation， 我们在forward pass 中已经计算出了 ， 我们将其存储在网络对应的节点中， 然后就可以直接计算出梯度课， 公式如下：

最后， 我们介绍整个的gradient descent algorithm, 如下(更新参数m 次）：

梯度检查和高级优化算法

BP 算法很难debug, 有很多的buggy implementation， 例如 off by one error in the indices。 对于这些buggy 的implementation， 很难看出出了问题， 因为结果仍然可能显示网络学习到了一些东西。 所以我们需要去numerically checking the derivative 来确保算法的implementation 是正确的。

办法如下， 对于每一个参数， 我们计算如下：

EPSILON 可以取一个很小的值， 例如： 10^(-4)， 使用BP算法的梯度为：

只需比较我们计算的量和BP中使用的量既可以判断是否出现问题。

熟了使用gradient descent 算法， 其他的advanced alogorithms 例如 conjugate gradient, L-BFGS 也可以用于最小化 J。

有了上述的基础， 下面说说autoencoders 和 sparsity。

autoencoder neural network 主要用于从unlabeled examples set  

萃取出特征。 一个autoencoder neural network 是一个unsupervised learning algorithm（无监督的学习算法）,  可以使用BP。 学习的目的就是使得输出和输入的数据尽可能的相等。

如下图自动编码机：

 

上述的自动编码机试图学习到一个函数不难看出一个trival 的solution 就是学习到一个identity function， 但是这并不是我们想要的的， 因为这样我们什么也没有学到。 但是通过给网络施加一些constraint， 或者给cost function 加一些限制项， 我们就能够避免学习到identity funcion。 

例如， 我们limiting the number of hidden units 我们就可以learn interesting structure about the data。 

举个例子， 我们有一幅 10 x 10 的图像，也就是100 pixels, 那么我们的输入层就有 n = 100 个输入。 假设我们限制hidden layer 为 50, 我们就可以强制我们的网络学习到 a compressed representation of the input。 利用这50维的数据， 我们可以尽可能的重建我们的输入图像。 如果输入的数据每一个是IID 的 gaussian independent features,  那么我们的compression task will be very difficult， 但是当我们的数据有一些structure的时候， 我们的算法就能够学习到这些correlation。

另外, 即使我们的hidden unit 的个数超过了输入向量的维度， 我们仍然可以学习到数据的稀疏表达。 方法就是我们在我们的training criterion 中加上 一个 sparsity constraint on the hidden units。

 我们记j th hidden unit 的 average activation(共m 和样本)如下：

我们记录我们希望的稀疏参数sparsity parameter 为， 这个值很小， 例如我们取0.05.我们希望这两个值相等：

换句话说， 我们希望the average acticvation of each hidden neuron j to be close to 0.05.

为了实现上述的稀疏性， 我们需要对我们的train criterion 加一个如下的penaliy term：

将二者看做是概率，上面的term 就是KL divergence:

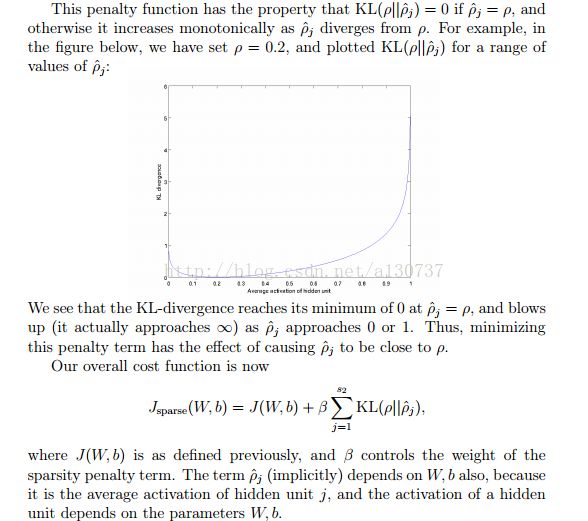
KL 有如下的性质：

这样， 我们的算法就变成了如下：

后面的剩下的详见NG的tutorial.

要看看我们的网络学习到了什么， 例如图像是 10 x 10， 我们如下处理， 通过将输入设为如下， 我们将得到最大的响应：

也就是将网络的所有的权重归一化后显示出来如下(50个hidden unit, 每一个hidden unit 学习一个feature，对应的是这个hidden unit 有100 个权重系数， 在reshape 成 10 x 10 展示出来， 所以共有50个 10 x 10 的 squares)：

代码后面贴上