ACM题目:skiing 分析与解答
描述
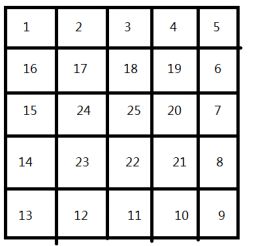
Michael喜欢滑雪百这并不奇怪, 因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待升降机来载你。Michael想知道载一个区域中最长底滑坡。区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
一个人可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-...-3-2-1更长。事实上,这是最长的一条。
输入
第一行表示有几组测试数据,输入的第二行表示区域的行数R和列数C(1 <= R,C <= 100)。下面是R行,每行有C个整数,代表高度h,0<=h<=10000。
后面是下一组数据;
输出
输出最长区域的长度。
样例输入
1
5 5
1 2 3 4 5
16 17 18 19 6
15 24 25 20 7
14 23 22 21 8
13 12 11 10 9
样例输出
25
分析:
首先要注意的是,该题目所问的是求最长的路径的长度,也由于该测试数据的原因,很多朋友会想到的一个思路是,从最高点出发,在四个方向中找到最递减最少的方向,以此类推,一直走到四个方向都不可以走的时候。这个思路的一个缺陷就是有时候,最长的路径并不一定是从最高点开始的,另外一个误区就是,每次减少高度最少的点也不一定是最长的路径,对于这两点一定要理解。
那么,怎么才能找到最长的路径呢?难道要以每一个地方都为起点来试一遍吗?是的,但是我们要做多一步,就是每当的走过一个地方,我们得知的它能走的路径长度了,将该长度记录下来,这样当下一次走到该点的时候,我们就可以直接得到答案而不用再次计算了。
具体方法便是,对每一个点进行遍历,在该点的四个方向中,对于满足不超过边界且比当前高度小的点进行递归,最后选出递归后返回值最大的值,将其+1便是当前点的路径最大值。
图解:
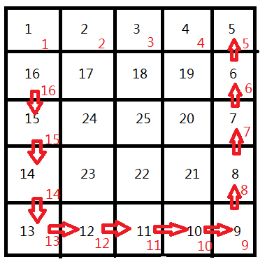
1.我们以测试数据为例:
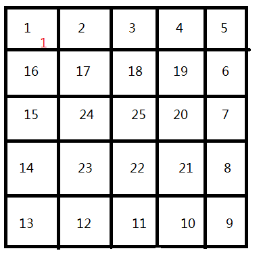
2.当遍历第一步的时候,发现没有其地方可以行走,记录当前的可走的最长路径为1
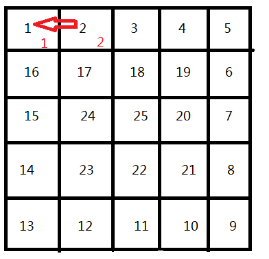
3.继续遍历,当走到第二部的时候,发现只能往左边走,走到1的位置时,发现1的长度为1,所以我们直接用1就可以。
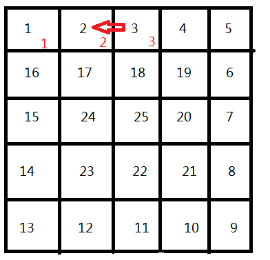
4.同理,走到3的位置时,便可以直接用2 的数据
5.依此类推,当遍历到第二行时,便能记录大量的点。在当以点17为起点时,就能发现这样节省了大量的时间。
源码:
#include
//#include
using namespace std;
int R, C,temp;
//本处的二维数组表示方向
const int dir[4][2] = { { -1, 0 }, { 1, 0 }, { 0, -1 }, { 0, 1 } };
struct Node
{
//建立节点类,value代表山的高度,path代表以该点为出发点,所能走的最长路径
int value;
int path;
};
Node map[100][100];
int LongestPath(int curRow , int curCol)
{
//如果当前的path有数值,则直接返回
if (map[curRow][curCol].path)return map[curRow][curCol].path;
int r, c,max= 0 ;
for (int i = 0; i < 4; i++)
{
r = curRow + dir[i][0]; c = curCol +dir[i][1];
if (r >= 0 && r < R && c >= 0 && c < C && map[r][c].value < map[curRow][curCol].value)
{
//将pos点的四个方向符合条件的进行递归,并记录返回的最大值
//注:这里的符合条件不是四个方向中最小的一个,而是比该点低的点都可以
//即对于四个方向的点存在比当前高度低的点都进行递归,选择一个数值最大做该点的最长路径
temp = LongestPath(r,c);
if (temp > max)max = temp;
}
}
map[curRow][curCol].path = max + 1;
return max + 1;
}
int main()
{
int n;
int i, j, k,max;
//ifstream cin("a.txt");
cin >> n;
for (i = 0; i < n; i++)
{
max = 0;
cin >> R >> C;
for (j = 0; j < R; j++)
{
//对所有点初始化
for (k = 0; k < C; k++){ cin >> map[j][k].value; map[j][k].path = 0; }
}
for (j = 0; j < R; j++)
{
for (k = 0; k < C; k++)
{
//对所有点遍历,选择一个最大值
temp=LongestPath(j,k);
if (temp > max)max = temp;
}
}
cout << max << endl;
}
//system("pause");
return 0;
}