决策树算法梳理
一、 信息论基础(熵 联合熵 条件熵 信息增益 基尼不纯度)
熵:
香农用信息熵的概念来描述信源的不确定度。
对于任意一个随机变量 X,它的熵定义如下:
![]()
变量的不确定性越大,熵也就越大,把它搞清楚所需要的信息量也就越大。
联合熵:
两个变量 X和Y的联合信息熵定义为:
![]()
联合熵表征了两事件同时发生系统的不确定度。
条件熵:
设有随机变量(X,Y),其联合概率分布为 p(X=x,Y= yi) = pij,i=1,2,…,n; j=1,2,…,m条件熵H(Y|X)表示在已知随机变量X的条件下随机变量Y的不确定性。随机变量X给定的条件下随机变量Y的条件熵H(Y|X),定义为X给定条件下,Y的条件概率分布的熵对X的数学期望
![]()
这里, ![]()
信息增益:
以使用划分前后集合熵的差值来衡量使用当前特征对于样本集合D划分效果的好坏。
划分前样本集合D的熵是一定的 ,entroy(前),
使用某个特征A划分数据集D,计算划分后的数据子集的熵 entroy(后)
信息增益 = entroy(前) - entroy(后)
书中公式:
![]()
做法:计算使用所有特征划分数据集D,得到多个特征划分数据集D的信息增益。
基尼指数(基尼不纯度):
基尼指数(基尼不纯度):表示在样本集合中一个随机选中的样本被分错的概率。
注意:Gini指数越小表示集合中被选中的样本被分错的概率越小,也就是说集合的纯度越高,反之,集合越不纯。
即 基尼指数(基尼不纯度)= 样本被选中的概率 * 样本被分错的概率
书中公式:

说明:
- pk表示选中的样本属于k类别的概率,则这个样本被分错的概率是(1-pk)
- 样本集合中有K个类别,一个随机选中的样本可以属于这k个类别中的任意一个,因而对类别就加和
- 当为二分类是,Gini§ = 2p(1-p)
样本集合D的Gini指数 : 假设集合中有K个类别,则:

二、 决策树的不同分类算法(ID3算法、C4.5、CART分类树)的原理及应用场景
ID3
ID3由Ross Quinlan在1986年提出。ID3决策树可以有多个分支,但是不能处理特征值为连续的情况。决策树是一种贪心算法,每次选取的分割数据的特征都是当前的最佳选择,并不关心是否达到最优。在ID3中,每次根据“最大信息熵增益”选取当前最佳的特征来分割数据,并按照该特征的所有取值来切分,也就是说如果一个特征有4种取值,数据将被切分4份,一旦按某特征切分后,该特征在之后的算法执行中,将不再起作用,所以有观点认为这种切分方式过于迅速。ID3算法十分简单,核心是根据“最大信息熵增益”原则选择划分当前数据集的最好特征,信息熵是信息论里面的概念,是信息的度量方式,不确定度越大或者说越混乱,熵就越大。在建立决策树的过程中,根据特征属性划分数据,使得原本“混乱”的数据的熵(混乱度)减少,按照不同特征划分数据熵减少的程度会不一样。在ID3中选择熵减少程度最大的特征来划分数据(贪心),也就是“最大信息熵增益”原则。下面是计算公式,建议看链接计算信息上增益的实例。

C4.5
C4.5是Ross Quinlan在1993年在ID3的基础上改进而提出的。.ID3采用的信息增益度量存在一个缺点,它一般会优先选择有较多属性值的Feature,因为属性值多的Feature会有相对较大的信息增益?(信息增益反映的给定一个条件以后不确定性减少的程度,必然是分得越细的数据集确定性更高,也就是条件熵越小,信息增益越大).为了避免这个不足C4.5中是用信息增益比率(gain ratio)来作为选择分支的准则。信息增益比率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的Feature。除此之外,C4.5还弥补了ID3中不能处理特征属性值连续的问题。

CART
CART(Classification and Regression tree)分类回归树由L.Breiman,J.Friedman,R.Olshen和C.Stone于1984年提出。ID3中根据属性值分割数据,之后该特征不会再起作用,这种快速切割的方式会影响算法的准确率。CART是一棵二叉树,采用二元切分法,每次把数据切成两份,分别进入左子树、右子树。而且每个非叶子节点都有两个孩子,所以CART的叶子节点比非叶子多1。相比ID3和C4.5,CART应用要多一些,既可以用于分类也可以用于回归。CART分类时,使用基尼指数(Gini)来选择最好的数据分割的特征,gini描述的是纯度,与信息熵的含义相似。CART中每一次迭代都会降低GINI系数。下图显示信息熵增益的一半,Gini指数,分类误差率三种评价指标非常接近。回归时使用均方差作为loss function。基尼系数的计算与信息熵增益的方式非常类似,公式如下
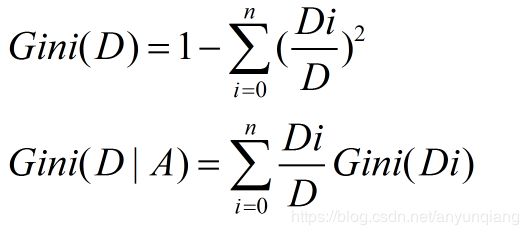
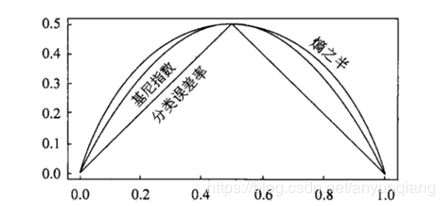
三、 回归树原理
最简单的模型
如果预测某个连续变量的大小,最简单的模型之一就是用平均值。比如同事的平均年龄是 28 岁,那么新来了一批同事,在不知道这些同事的任何信息的情况下,直觉上用平均值 28 来预测是比较准确的,至少比 0 岁或者 100 岁要靠谱一些。我仍然是预测同事年龄,这次我们预先知道了同事的职级,假设职级的范围是整数1-10,如何能让这个信息帮助我们更加准确的预测年龄呢?
一个思路是根据职级把同事分为两组,这两组分别应用我们之前提到的“平均值”模型。比如职级小于 5 的同事分到A组,大于或等于5的分到 B 组,A 组的平均年龄是 25 岁,B 组的平均年龄是 35 岁。如果新来了一个同事,职级是 3,应该被分到 A 组,我们就预测他的年龄是 25 岁。
最佳分割点
还有一个问题待解决,如何取一个最佳的分割点对不同职级的同事进行分组呢?
我们尝试所有 m 个可能的分割点 P_i,沿用之前的损失函数,对 A、B 两组分别计算 Loss 并相加得到 L_i。最小的 L_i 所对应的 P_i 就是我们要找的“最佳分割点”。
运用多个变量
再复杂一些,如果我们不仅仅知道了同事的职级,还知道了同事的工资(貌似不科学),该如何预测同事的年龄呢?
我们可以分别根据职级、工资计算出职级和工资的最佳分割点P_1, P_2,对应的Loss L_1, L_2。然后比较L_1和L2,取较小者。假设L_1 < L_2,那么按照P_1把不同职级的同事分为A、B两组。在A、B组内分别计算工资所对应的分割点,再分为C、D两组。这样我们就得到了AC, AD, BC, BD四组同事以及对应的平均年龄用于预测。
答案揭晓
如何实现这种1 to 2, 2 to 4, 4 to 8的算法呢?
熟悉数据结构的同学自然会想到二叉树,这种树被称为回归树,顾名思义利用树形结构求解回归问题。
四、 决策树防止过拟合手段
原因1:样本问题
(1)样本里的噪音数据干扰过大,大到模型过分记住了噪音特征,反而忽略了真实的输入输出间的关系;(什么是噪音数据?)
(2)样本抽取错误,包括(但不限于)样本数量太少,抽样方法错误,抽样时没有足够正确考虑业务场景或业务特点,等等导致抽出的样本数据不能有效足够代表业务逻辑或业务场景;
(3)建模时使用了样本中太多无关的输入变量。
解决办法:合理、有效地抽样,用相对能够反映业务逻辑的训练集去产生决策树。
原因2:构建决策树的方法问题
在决策树模型搭建中,我们使用的算法对于决策树的生长没有合理的限制和修剪的话,决策树的自由生长有可能每片叶子里只包含单纯的事件数据或非事件数据,可以想象,这种决策树当然可以完美匹配(拟合)训练数据,但是一旦应用到新的业务真实数据时,效果是一塌糊涂。
解决方法:
针对原因1的解决方法:剪枝:提前停止树的增长或者对已经生成的树按照一定的规则进行后剪枝
五、 模型评估
保持方法
在保持(Holdout)方法中,将被标记的原始数据划分成两个不想交的集合,分别称为训练集合检验集。在训练数据集上归纳分类模型,在检验集上评估模型的性能。训练集和检验集的划分比例通常根据分析家的判断(例如,50-50,或者2/3作为训练集、1/3作为检验集)。分类器的准确率根据模型在检验集上的准确率估计。
随机二次抽样
可以多次重复保持方法来改进对分类器性能的估计,这种方法称作随机二次抽样(random subsampling)。设acciacci是第ii次迭代的模型准确率,总准确率是 。随机二次抽样也会遇到一些与保持方法同样的问题,因为在训练阶段也没有利用尽可能多的数据。并且,由于它没有控制每个记录用于训练和检验的次数,因此,有些用于训练的记录使用的频率可能比其他记录高很多。
交叉验证
替代随机二次抽样的一种方法是交叉验证(cross-validation)。在该方法中,每个记录用于训练的次数相同,并且恰好检验一次。为了解释该方法,假设把数据分为相同大小的两个子集,首先,我们选择一个子集作训练集,而另一个作检验集,然后交换两个集合的角色,原先作训练集的现在做检验集,反之亦然,这种方法叫做二折交叉验证。总误差通过对两次运行的误差求和得到。在这个例子中,每个样本各作一次训练样本和检验样本。k折交叉验证是对该方法的推广,把数据分为大小相同的k份,在每次运行,选择其中一份作检验集,而其余的全作为训练集,该过程重复k次,使得每份数据都用于检验恰好一次。同样,总误差是所有k次运行的误差之和。
六、 sklearn参数详解,Python绘制决策树
class sklearn.tree.DecisionTreeClassifier(criterion=‘gini’, splitter=‘best’, max_depth=None, min_samples_split=2,min_samples_leaf =1, min_weight_fraction_leaf=0.0, max_features=None, random_state=None, max_leaf_nodes=None,class_weight=None, presort=False)
criterion:string类型,可选(默认为"gini")
衡量分类的质量。支持的标准有"gini"代表的是Gini impurity(不纯度)与"entropy"代表的是information gain(信息增益)。
splitter:string类型,可选(默认为"best")
一种用来在节点中选择分类的策略。支持的策略有"best",选择最好的分类,"random"选择最好的随机分类。
max_features:int,float,string or None 可选(默认为None)
在进行分类时需要考虑的特征数。
1.如果是int,在每次分类是都要考虑max_features个特征。
2.如果是float,那么max_features是一个百分率并且分类时需要考虑的特征数是int(max_features*n_features,其中n_features是训练完成时发特征数)。
3.如果是auto,max_features=sqrt(n_features)
4.如果是sqrt,max_features=sqrt(n_features)
5.如果是log2,max_features=log2(n_features)
6.如果是None,max_features=n_features
注意:至少找到一个样本点有效的被分类时,搜索分类才会停止。
max_depth:int or None,可选(默认为"None")
表示树的最大深度。如果是"None",则节点会一直扩展直到所有的叶子都是纯的或者所有的叶子节点都包含少于min_samples_split个样本点。忽视max_leaf_nodes是不是为None。
min_samples_split:int,float,可选(默认为2)
区分一个内部节点需要的最少的样本数。
1.如果是int,将其最为最小的样本数。
2.如果是float,min_samples_split是一个百分率并且ceil(min_samples_split*n_samples)是每个分类需要的样本数。ceil是取大于或等于指定表达式的最小整数。
min_samples_leaf:int,float,可选(默认为1)
一个叶节点所需要的最小样本数:
1.如果是int,则其为最小样本数
2.如果是float,则它是一个百分率并且ceil(min_samples_leaf*n_samples)是每个节点所需的样本数。
min_weight_fraction_leaf:float,可选(默认为0)
一个叶节点的输入样本所需要的最小的加权分数。
max_leaf_nodes:int,None 可选(默认为None)
在最优方法中使用max_leaf_nodes构建一个树。最好的节点是在杂质相对减少。如果是None则对叶节点的数目没有限制。如果不是None则不考虑max_depth.
class_weight:dict,list of dicts,“Banlanced” or None,可选(默认为None)
表示在表{class_label:weight}中的类的关联权值。如果没有指定,所有类的权值都为1。对于多输出问题,一列字典的顺序可以与一列y的次序相同。
"balanced"模型使用y的值去自动适应权值,并且是以输入数据中类的频率的反比例。如:n_samples/(n_classes*np.bincount(y))。
对于多输出,每列y的权值都会想乘。
如果sample_weight已经指定了,这些权值将于samples以合适的方法相乘。
random_state:int,RandomState instance or None
如果是int,random_state 是随机数字发生器的种子;如果是RandomState,random_state是随机数字发生器,如果是None,随机数字发生器是np.random使用的RandomState instance.
persort:bool,可选(默认为False)
是否预分类数据以加速训练时最好分类的查找。在有大数据集的决策树中,如果设为true可能会减慢训练的过程。当使用一个小数据集或者一个深度受限的决策树中,可以减速训练的过程。