leetcode 经典 图相关题目(思路、方法、code)
图的问题基本就是 BFS和DFS,还有拓扑排序、最短路、最小生成树,有时也会用并查集进行分类,还要注意节点的入度出度等特征。
文章目录
- [207. 课程表](https://leetcode-cn.com/problems/course-schedule/)
- [210. 课程表 II](https://leetcode-cn.com/problems/course-schedule-ii/)
- [684. 冗余连接](https://leetcode-cn.com/problems/redundant-connection/)
- [785. 判断二分图](https://leetcode-cn.com/problems/is-graph-bipartite/)
- [997. 找到小镇的法官](https://leetcode-cn.com/problems/find-the-town-judge/)
- [841. 钥匙和房间](https://leetcode-cn.com/problems/keys-and-rooms/)
- [面试题 04.01. 节点间通路](https://leetcode-cn.com/problems/route-between-nodes-lcci/)
- [1306. 跳跃游戏 III](https://leetcode-cn.com/problems/jump-game-iii/)
207. 课程表
你这个学期必须选修 numCourse 门课程,记为 0 到 numCourse-1 。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们:[0,1] 给定课程总量以及它们的先决条件,请你判断是否可能完成所有课程的学习?
示例 1:
输入: 2, [[1,0]]
输出: true
解释: 总共有 2 门课程。学习课程 1 之前,你需要完成课程 0。所以这是可能的。
示例 2:
输入: 2, [[1,0],[0,1]]
输出: false
解释: 总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0;并且学习课程 0 之前,你还应先完成课程 1。这是不可能的。
分析:(这个题让我直接联想到死锁检测 QAQ )
这个题实际上是有向图,我们判断这些课程是否可以完成,实际上就是要判断该有向图是否有环,如果有向图有环,则说明不可以完成全部课程,反之则可以完成全部课程。
方法一:拓扑排序(拓扑排序在有向图问题判断环中经常使用)
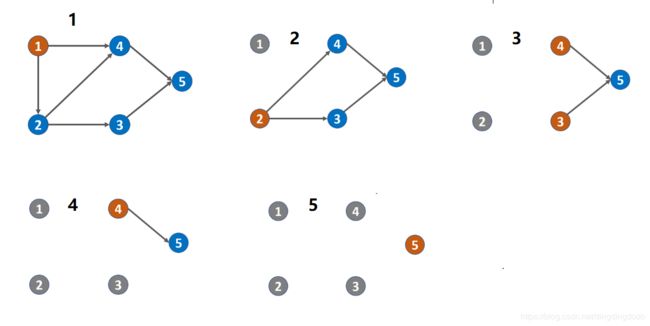
利用入度表的BFS(入度:可以简单理解为箭头指向自己的数量),进行宽度优先搜索,只将入读为0的点添加到队列。当完成一个顶点的搜索时(将该点从队列中pop出),将该顶点指向的所有顶点入度减1(等价于将该顶点从图中移除),如果有新的节点入度变为0,则将其加入队列。以次进行,如果宽搜完成后,如果所有入度都为0,则图无环,否则说明有环。
如图所示,最终全部入度为0,故无环。如果有环,会发现部分位置的入度始终大于0。
代码:
class Solution
{
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites)
{
vector<int> degree(numCourses); //入度表
vector<vector<int>> Graph; //临界矩阵 用vector表示的话不用存没有关系的位置值
vector<int> v;
for(int i=0;i<numCourses;i++)
{
degree.push_back(0); //初始化degree和Graph
Graph.push_back(v);
}
for(int i=0;i<prerequisites.size();i++) //将 prerequisites信息处理为degree和Graph的信息
{
degree[prerequisites[i][0]]++; //[1,0]表示学1前需要学0,就是0指向1,故[a,b]中a的入度加1
Graph[prerequisites[i][1]].push_back(prerequisites[i][0]); //0指向1,故0的指向节点中加上1
}
queue<int> Q; //队列
for(int i=0;i<numCourses;i++)
{
if(degree[i]==0) Q.push(i);//
}
int nums=0; //记录入度为0的点
while(!Q.empty()) //BFS的方法
{
int tmp=Q.front();
Q.pop();
nums++;
for(int i=0;i<Graph[tmp].size();i++)
{
degree[Graph[tmp][i]]--; //将指向的节点的入度减1
if(degree[Graph[tmp][i]]==0)//直接在这里判断是否入度变为0了,这样避免了每次遍历所有degree数组并且不用标记是否遍历过了
Q.push(Graph[tmp][i]); //如果入度为0加入队列
}
}
if(nums==numCourses) return true;
else return false;
}
};
210. 课程表 II
现在你总共有 n 门课需要选,记为 0 到 n-1。
在选修某些课程之前需要一些先修课程。 例如,想要学习课程 0 ,你需要先完成课程 1 ,我们用一个匹配来表示他们: [0,1]
给定课程总量以及它们的先决条件,返回你为了学完所有课程所安排的学习顺序。
可能会有多个正确的顺序,你只要返回一种就可以了。如果不可能完成所有课程,返回一个空数组。
示例 1:
输入: 2, [[1,0]]
输出: [0,1]
解释: 总共有 2 门课程。要学习课程 1,你需要先完成课程 0。因此,正确的课程顺序为 [0,1] 。
分析:实际上,利用拓扑排序,采用入度为0的点依次入队列的方式,最终如果没有环路,则出队列的顺序,其实就是一种可行的上课策略,因为每次选择的课程都是没有先决课程的(因为将其入队列时入度为0,故可以视为没有先修课程的限制,就算有也可以将先修课程完成),因此在上个问题的基础上,调整输出即可。
class Solution {
public:
vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites)
{
vector<int> degree(numCourses); //入度表
vector<vector<int>> Graph; //临界矩阵 用vector表示的话不用存没有关系的位置值
vector<int> v;
for(int i=0;i<numCourses;i++)
{
degree.push_back(0); //初始化degree和Graph
Graph.push_back(v);
}
for(int i=0;i<prerequisites.size();i++) //将 prerequisites信息处理为degree和Graph的信息
{
degree[prerequisites[i][0]]++; //[1,0]表示学1前需要学0,就是0指向1,故[a,b]中a的入度加1
Graph[prerequisites[i][1]].push_back(prerequisites[i][0]); //0指向1,故0的指向节点中加上1
}
queue<int> Q; //队列
for(int i=0;i<numCourses;i++)
{
if(degree[i]==0) Q.push(i);//
}
int nums=0; //记录入度为0的点
vector<int> result;
while(!Q.empty()) //BFS的方法
{
int tmp=Q.front();
Q.pop();
result.push_back(tmp);
nums++;
for(int i=0;i<Graph[tmp].size();i++)
{
degree[Graph[tmp][i]]--; //将指向的节点的入度减1
if(degree[Graph[tmp][i]]==0)//直接在这里判断是否入度变为0了,这样避免了每次遍历所有degree数组并且不用标记是否遍历过了
Q.push(Graph[tmp][i]); //如果入度为0加入队列
}
}
if(nums==numCourses) return result;
else return {};
}
};
684. 冗余连接
在本问题中, 树指的是一个连通且无环的无向图。输入一个图,该图由一个有着N个节点 (节点值不重复1, 2, …, N) 的树及一条附加的边构成。附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ,满足 u < v,表示连接顶点u 和v的无向图的边。
返回一条可以删去的边,使得结果图是一个有着N个节点的树。如果有多个答案,则返回二维数组中最后出现的边。答案边 [u, v] 应满足相同的格式 u < v。
示例 1:
输入: [[1,2], [1,3], [2,3]]
输出: [2,3]
解释: 给定的无向图为:
1
/ \
2 - 3
示例 2:
输入: [[1,2], [2,3], [3,4], [1,4], [1,5]]
输出: [1,4]
解释: 给定的无向图为:
5 - 1 - 2
| |
4 - 3
分析:该题实际上是考察的是,如果当前给定的边已经令A,B可以连通,则新的边
因此,很显然可以用并查集进行处理。 并查集可以参考一文搞定并查集
每次给定一个边后,判断该边所指的两个点是否已经连通(即是否已经在并查集的同一个类别中),如果是说明改边冗余,否则将该边所指的两个点连通起来。
(这里的并查集代码是具有优化策略的并查集代码,因为该题数据较小其实不需要考虑rank进行优化,但总体并查集代码是固定的,学会该优化的即可)
class Solution {
public:
int par[1001]; //父节点, 存储该节点对应的根节点的位置
int rank[1001]; //树的高度,存储该树的位置
void init(int n) //初始化n个元素,使得该n个元素最初的根节点均为自身
{
for(int i=0;i<n;i++)
{
par[i]=i;
rank[i]=0;
}
}
int find (int x) //查询第x个节点所在树的根
{
if(par[x]==x)
return x;
else
return par[x]=find(par[x]); //这一步很巧妙,既通过递归找到根节点,又同时完成了路径的压缩
}
void unite(int x,int y) //将x和y所在的集合合并
{ //合并时主要考虑两个根即可
x=find(x);
y=find(y);
if(x==y) return ; //在同一集合,不需操作
if(rank[x]<rank[y]) //rank大的节点作为合并后的根节点
par[x]=y;
else
{
if(rank[x]==rank[y]) rank[x]++; //如果两个树高度一样,则合并后树的高度加1
par[y]=x;
}
}
bool same(int x,int y) //判断x和y是否是同一个集合
{
return find(x)==find(y);
}
vector<int> findRedundantConnection(vector<vector<int> >& edges)
{
// vector result;
init(1001);
for(int i=0;i<edges.size();i++)
{
if(same(edges[i][0],edges[i][1])) //如果当前两个点已经在一个集合,返回即可
return edges[i];
else
unite(edges[i][0],edges[i][1]);
}
return edges[0];
}
};
785. 判断二分图
给定一个无向图graph,当这个图为二分图时返回true。
如果我们能将一个图的节点集合分割成两个独立的子集A和B,并使图中的每一条边的两个节点一个来自A集合,一个来自B集合,我们就将这个图称为二分图。
graph将会以邻接表方式给出,graph[i]表示图中与节点i相连的所有节点。每个节点都是一个在0到graph.length-1之间的整数。这图中没有自环和平行边: graph[i] 中不存在i,并且graph[i]中没有重复的值。
示例 1:
输入: [[1,3], [0,2], [1,3], [0,2]]
输出: true
解释:
无向图如下:
0----1
| |
| |
3----2
我们可以将节点分成两组: {0, 2} 和 {1, 3}。
示例 2:
输入: [[1,2,3], [0,2], [0,1,3], [0,2]]
输出: false
解释:
无向图如下:
0----1
| \ |
| \ |
3----2
我们不能将节点分割成两个独立的子集。
分析:判断二分图问题也就是着色问题,目的是希望用两种颜色涂所有节点,使得所有相邻节点的颜色都不一样。因此,我们可以用三种状态进行标注:分别表示没有涂色,涂红色,涂蓝色。
- 通过DFS或者BFS进行遍历图
- 如果起始点没有涂色,则可以任意将其涂一种颜色
- 遍历时,将相邻节点涂成与当前节点不同的颜色,如果相邻节点已经涂色且与自己颜色相同,说明不可以二分
- 直至涂色结束
代码:(用的是BFS搜索,由于图可能是非连通图,因此需要逐一判断是否每个点都遍历过了)
class Solution {
public:
int color[101];
bool isBipartite(vector<vector<int>>& graph)
{
queue<int> Q;//bfs的队列
for(int j=0;j<graph.size();j++)
{
if(color[j]==0)
{
Q.push(j);
color[j]=1; //没有涂色的话将其置为1的颜色
}
else
continue;
while(!Q.empty())
{
int tmp=Q.front();
Q.pop();
int now_color=(color[tmp]==1?2:1); //表示相邻节点应该涂的颜色
for(int i=0;i<graph[tmp].size();i++)
{
if(color[graph[tmp][i]]==0)
{
color[graph[tmp][i]]=now_color;
Q.push(graph[tmp][i]); //只在涂色时将其加入
}
else if(color[graph[tmp][i]]==color[tmp])
return false;
else
continue;
}
}
}
return true;
}
};
997. 找到小镇的法官
在一个小镇里,按从 1 到 N 标记了 N 个人。传言称,这些人中有一个是小镇上的秘密法官。
如果小镇的法官真的存在,那么:
-
小镇的法官不相信任何人。
-
每个人(除了小镇法官外)都信任小镇的法官。
-
只有一个人同时满足属性 1 和属性 2 。
给定数组 trust,该数组由信任对 trust[i] = [a, b] 组成,表示标记为 a 的人信任标记为 b 的人。
如果小镇存在秘密法官并且可以确定他的身份,请返回该法官的标记。否则,返回 -1。
示例 1:
输入:N = 2, trust = [[1,2]]
输出:2
示例 2:
输入:N = 3, trust = [[1,3],[2,3]]
输出:3
示例 3:
输入:N = 3, trust = [[1,3],[2,3],[3,1]]
输出:-1
分析:将输入可视化,如果A信任B,则从A向B画一个箭头,因此,法官应当是这样一个人:所有其他人都有指向他的箭头,他没有指向任何人的箭头。很显然,**可以将其视为有向图中的入度和出度问题,法官的入度应当为 n − 1 n-1 n−1 ,出度应当为 0 0 0 . ** 分析易得,只需要存储总度即可,即入度-出度,如果出度则总度减1,入度则总度加1,因此如果有法官,其度应当为N-1,其他人的度一定小于N-1
代码如下:
class Solution {
public:
int findJudge(int N, vector<vector<int> >& trust)
{
vector<int> degree(N+1); //入度
for(int i=0;i<trust.size();i++)
{
degree[trust[i][1]]++;
degree[trust[i][0]]--;
}
for(int i=1;i<=N;i++)
{
if(indegree[i]==N-1)
return i;
}
return -1;
}
};
841. 钥匙和房间
有 N 个房间,开始时你位于 0 号房间。每个房间有不同的号码:0,1,2,…,N-1,并且房间里可能有一些钥匙能使你进入下一个房间。
在形式上,对于每个房间 i 都有一个钥匙列表 rooms[i],每个钥匙 rooms[i] [j] 由 [0,1,…,N-1] 中的一个整数表示,其中 N = rooms.length。 钥匙 rooms[i] [j] = v 可以打开编号为 v 的房间。
最初,除 0 号房间外的其余所有房间都被锁住。你可以自由地在房间之间来回走动。
如果能进入每个房间返回 true,否则返回 false。
示例 1:
输入: [[1],[2],[3],[]]
输出: true
解释:
我们从 0 号房间开始,拿到钥匙 1。
之后我们去 1 号房间,拿到钥匙 2。
然后我们去 2 号房间,拿到钥匙 3。
最后我们去了 3 号房间。
由于我们能够进入每个房间,我们返回 true。
分析:该题实际上是判断从一点出发,该图是否是连通的。考虑用BFS或者DFS遍历,从房间0出发,将获得的钥匙的房间依次遍历,最终如果所有房间都可以进入,则返回true.
代码:BFS
class Solution {
public:
bool canVisitAllRooms(vector< vector<int> >& rooms)
{
int num=rooms.size();
vector<bool> visit(num); //标记是否访问过
for(int i=0;i<num;i++)
{
visit[i]=false;
}
int ans=1; //记录已经访问过的房间数量
queue<int> Q;
Q.push(0); //进入0房间
visit[0]=true;
while(!Q.empty())
{
int tmp=Q.front();
Q.pop();
for(int i=0;i<rooms[tmp].size();i++)
{
if(visit[rooms[tmp][i]]==false) //添加新房间时直接更新visit和ans
{
Q.push(rooms[tmp][i]);
visit[rooms[tmp][i]]=true;
ans++;
}
}
if(ans==num) return true;
}
return false;
}
};
面试题 04.01. 节点间通路
节点间通路。给定有向图,设计一个算法,找出两个节点之间是否存在一条路径
提示:
- 节点数量n在[0, 1e5]范围内。
- 节点编号大于等于 0 小于 n。
- 图中可能存在自环和平行边
示例1:
输入:n = 3, graph = [[0, 1], [0, 2], [1, 2], [1, 2]], start = 0, target = 2
输出:true
示例2:
输入:n = 5, graph = [[0, 1], [0, 2], [0, 4], [0, 4], [0, 1], [1, 3], [1, 4], [1, 3], [2, 3], [3, 4]], start = 0, target = 4
输出 true
分析:采用邻接矩阵+BFS的方式遍历,需要采用一个数组标记是否已经访问过,将一个节点加入队列时就直接将访问数组进行标记,避免多次将其添加。
class Solution {
public:
bool findWhetherExistsPath(int n, vector< vector<int> >& graph, int start, int target)
{
vector< vector<int> > Graph(n); //邻接矩阵
for(int i=0;i<graph.size();i++)
Graph[graph[i][0]].push_back(graph[i][1]);
queue<int> Q; //BFS的队列
bool visit[n]; //标记数组
for(int i=0;i<n;i++)
visit[i]=false;
Q.push(start);
visit[start]=true;
while(!Q.empty())
{
int tmp=Q.front();
Q.pop();
for(int i=0;i<Graph[tmp].size();i++)
{
if(visit[Graph[tmp][i]]==false)
{
if(Graph[tmp][i]==target) return true;
visit[Graph[tmp][i]]=true;
Q.push(Graph[tmp][i]);
}
}
}
return false;
}
};
1306. 跳跃游戏 III
这里有一个非负整数数组 arr,你最开始位于该数组的起始下标 start 处。当你位于下标 i 处时,你可以跳到 i + arr[i] 或者 i - arr[i]。
请你判断自己是否能够跳到对应元素值为 0 的 任意 下标处。
注意,不管是什么情况下,你都无法跳到数组之外。
示例 1:
输入:arr = [4,2,3,0,3,1,2], start = 5
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 5 -> 下标 4 -> 下标 1 -> 下标 3
下标 5 -> 下标 6 -> 下标 4 -> 下标 1 -> 下标 3
示例 2:
输入:arr = [4,2,3,0,3,1,2], start = 0
输出:true
解释:
到达值为 0 的下标 3 有以下可能方案:
下标 0 -> 下标 4 -> 下标 1 -> 下标 3
示例 3:
输入:arr = [3,0,2,1,2], start = 2
输出:false
解释:无法到达值为 0 的下标 1 处。
分析:注意该跳跃游戏中,在某个位置,只可以跳到 i + arr[i] 或者 i - arr[i]的位置,因此,实际上可以将其视为一个有向图,如果一个点可以跳到一个位置,则说明可以形成一个有向边。故该问题,转换成了从与上一个问题类似的问题,即从起始点出发能否达到值为0的位置。依旧采用 BFS 的方式,采用一个 visit 表示是否已经访问过。在这里不显示创建邻接矩阵了,因为每一个点能到达的至多为两个位置,故就在BFS搜索时遍历即可。(注意的是,为0的点可能有很多,只需要到达一个即可)
class Solution {
public:
bool canReach(vector<int>& arr, int start)
{
int size=arr.size();
bool visit[size];
vector<int> target;
for(int i=0;i<size;i++)
{
visit[i]=false;
if(arr[i]==0) target.push_back(i); //找到target都在哪里
}
if(find(target.begin(),target.end(),start)!=target.end()) return true;
queue<int> Q;
Q.push(start);
visit[start]=true;
while(!Q.empty())
{
int tmp=Q.front();
Q.pop();
if(tmp-arr[tmp]>=0&&visit[tmp-arr[tmp]]==false)
{
if(find(target.begin(),target.end(),tmp-arr[tmp])!=target.end()) return true;
Q.push(tmp-arr[tmp]);
visit[tmp-arr[tmp]]=true;
}
if(tmp+arr[tmp]<size&&visit[tmp+arr[tmp]]==false)
{
if(find(target.begin(),target.end(),tmp+arr[tmp])!=target.end()) return true;
Q.push(tmp+arr[tmp]);
visit[tmp+arr[tmp]]=true;
}
}
return false;
}
};