机器学习基础01-线性代数

数学基础内容与学习路线

week1:线性代数

被人誉为21世纪的数学，在机器学习当中十分重要，机器学习中很多算法都是用线性代数来表示的，这样会使得数据和算法十分简洁，降低复杂度。

• 标量、向量与矩阵，矩阵的运算
• 线性相关与线性无关，矩阵的秩
• 矩阵的范数与迹
• 矩阵变换、矩阵分解
• PCA推导

week2:微积分

微积分是高等数学的基础，也是机器学习的基础，机器学习中会使用到微分和积分

• 集合与函数
• 极限
• 连续函数和微分
• 积分
• 矩阵的求导与Hessian矩阵

week3:概率论+统计

有人说机器学习就是统计学习方法，机器学习确实是以统计学为基础的

• 概率论基础
• 常用概率分布
• 联合分布与边缘分布
• 条件概率
• 期望与方差

week4:概率论+信息论

交叉熵损失函数是最常用的基于信息论的

• 极大似然估计与最大后验估计
• 贝叶斯法则
• 信息的度量
• 信息熵、互信息
• KL散度（相对熵）

week5:优化方法

比较难。当我们得到了约束条件之后，我们必须使用优化方法得到问题的最优解，在线性回归中，使用最小二乘法得到所有点到直线的最短距离就是一个最常用的优化方法。

• 最速下降法
• 梯度下降法
• 牛顿下降法、拟牛顿法
• 共轭梯度法
• adman方法
• 拉格朗日乘数法

学习数学基础的建议

• 重视基础概念和定理
• 不过多纠结具体证明过程
• 遇到问题多与其他人交流
• 两本书：
  • 花书、数学之美第2版

标量、向量与矩阵

要求掌握：

• 标量与向量
• 向量运算
• 矩阵定义
• 矩阵运算
• 特殊矩阵

标量与向量

• 向量的元素个数就是维度，如[1,5,8,3,2]就是5维的
• 标量是一个单独的数，一个用斜体普通小写字母或希腊字母表示，如a
• 向量是一个同时具有大小和方向的几何对象，一般用粗体小写字母来表示向量，小写字母上有一个小箭头，这才是向量的一般表示法$a$。
• 向量(vector)：一个向量是一列数。这些数是有序排列的。通过次序中的索引，我们可以确定每个单独的数。通常我们赋予向量粗估的小写变量名称，比如 x。向量中的元素可以通过带脚标的斜体表示。向量a中的第一个元素是a1,第2个元素是a2…我们也会注明存储在向量中的元素是什么类型的，如果每个元素都属于实数R，并且该向量有n个元素，那么该向量属于实数集R的n次笛卡尔积构成的集合，记为R^n。当需要明确表示向量中的元素时，我们会将元素排列成一个方括号包围的纵列：
  [x1]
  [x2]
  [x3]
  …
  [xn]
  我们可以把向量看作空间中的点，每个元素是不同坐标轴上的坐标。
  有时我们需要索引向量中的一些元素。在这种情况下，我们定义一个包含这些元素索引的集合，然后将该集合写在脚标处，比如指定x1,x3,x6，我们定义交叉集合S={1,3,6}，然后写做$x_S$。我们用符号-表示集合的补集中的索引。比如$x_{-1}$表示x中除$x_1$之外的所有元素。x_{-S}表示x中除x1,x3,x6之外的所有元素构成的向量

向量的表示

• 向量一般用粗体小写字母或希腊字母表示，如x等（有时也会用箭头来标识），其元素记作$x_i$
• 向量分类：
  • 行向量
  • 列向量

向量的一般属性

• 向量的模：所有元素的平方和再开方
• 向量的范数：$||a|{|}_1$,$||a|{|}_2$,$||a|{|}_{\infty }$
  • 1范数，各元素绝对值的和
  • 2范数，就是向量的模，各元素平方和再开方。如果没有下标，默认为2范数
  • 无穷范数，所有元素绝对值中取最大

向量运算

• 形状不同的向量不能运算

• 向量的加法：等于各元素相加

• 向量的乘积–点积（代数定义）：

  • 点积：两个形状一样的向量，各位置的元素相乘之后求和，ab还能写成|ab^T|，其中T表示转置，而||表示行列式。
  • 元素乘/数乘：一个向量和一个标量相乘，等于向量中的各元素与标量相乘。

• 向量的乘积–点积（几何定义）
  在欧氏空间中，点积可以直观地定义为：
  $a\ast b=|a|\ast |b|cos\theta$, ||表示向量的模，\thta表示 两个向量之间的角度。

欧氏空间中的向量A在向量B上的标量投影是指：
$A_B=|A|cos\theta$

• 向量的乘积–点积（高维空间的定义方式）

矩阵定义

• 为什么要学习矩阵？ 机器学习基础公式：$y=f(x)=x{w}^T+b$ ，即可以用来表示线性回归模型，也可以表示神经网络中的前向传播，公式中的w,b,x都是向量或者矩阵。
• 矩阵(matrix)：矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个）所确定。我们通常会赋予矩阵 粗体的大写变量名称，比如A（向量是小写的粗体，标量是小写非粗体）。如果一个实数矩阵高度为m，宽度为n，那么我们说A属于$R^{m\ast n}$。我们在表示矩阵中的元素时，通常以不加粗的斜体表示，索引用逗号间隔。比如，$A_{1,1}$表示矩阵A左上的元素，$A_{m,n}$表示A右下的元素。我们通过用冒号：表示水平坐标，以表示垂直坐标i中的所有元素。比如，$A_{i,:}$表示A中垂直坐标i上的一横排元素。这也被称为A的第i行，同样地，$A_{:,i}$表示A的第i列。
• 有时我们需要矩阵值表达式的索引 ，而不是单个元素。在这种情况下，我们在表达式后面接下标，但不必将矩阵的变量名小写化。比如，$f(A{)}_{i,j}$表示函数f作用在A上之后输出的矩阵的第i行第j列元素。

矩阵运算

• 矩阵加法，矩阵的形状一样，相加就是对应位置的元素相加。满足结合律和交换律
• 矩阵乘法
  • 点积，标准积
    • 两个矩阵$A(m,n)$,$B(n,k)$，只有前一个矩阵的列数和后一个矩阵的行数相等时，才能相乘。结果的形状是m,k（其实这里换成向量也是一样的）
    • 书上的定义：矩阵乘法是矩阵运算中最重要的操作之一。两个矩阵A和B的矩阵乘积(matrix product)是第三个矩阵C。为了使乘法定义良好，矩阵A的列数必须和矩阵B的行数相等。如果矩阵A的形状是mn，矩阵B的形状是np,那么C的形状就是m*p。可以通过将两个或多个矩阵并列放置以书写矩阵乘法，例如：$C=AB$
      具体地，该乘法操作定义为：$C_{i,j}={\sum }_k{A}_{i,k}{B}_{k,j}$
  • 元素积，对应元素的乘积就是元素积，形状一样才能元素积。
• 矩阵的转置
  • 矩阵的重要操作之一。矩阵转置就是以对角线为轴的镜像，从左上角到右下角的对角线为主对角线。矩阵A的转置表示为$A^T$，定义：$(A^T{)}_{i,j}=A_{j,i}$。矩阵的转置可以看成以主对角线为轴的一个镜像。
  • 向量可以看成只有一列的矩阵（默认的向量就是列向量！），向量的转置可以看作只有一行的矩阵，有时我们可以通过将向量元素作为行矩阵写在文本行中，然后使用转置操作将其变为标准的列向量，来定义一个向量，比如$ \bold x=[x1,x2,x3]^T$
  • 标量可以看作只有一个元素的矩阵，因此标量的转置等于它本身。

特殊矩阵

• 全0矩阵：全是0
• 全1矩阵：全是1
• 对角矩阵：除了对角线之外其他全是0的方阵
• 单位矩阵：对角线上全是1，其他全是0的方阵
• 上三角矩阵：对角线和上方之外全是0的方阵
• 下三角矩阵：对角线和下方之外全是0的方阵

线性相关性与矩阵的秩

线性组合与线性表示

• 定义1：给定n给向量$b,a1,a2,...,am$，（$b,a1,a2,...am$都是向量）如果存在一组数$k1,k2,...,km$，使得$b=k1a1+k2a2+...+kmam$，则称向量b是向是组a1,a2,…,am的线性组合，或称b可由向量组a1,a2,…,am线性表示。
• 例：任何一个n维向量a都是n维向量组(1,0,…,0)(0,1,…,0)…(0,0,…,1)的线性组合。其中$b=k$
• 例：0向量是任何一组向量的线性组合。其中$b=k=0$
• 例：向量组a1,a2,…,am中的任一向量ai(1<=i<=m)都是此向量组的线性组合。$ai=0\ast a1+...+1\ast ai+...+0\ast am$
• 注：并非每一个向量都可以表示成某几个向量的线性组合
• 注：一个向量可以由一组向量线性表示，但表示 式却未必唯一。如：$a1=(1,2,3)a2=(-1,1,4)a3=(3,3,2)b=(4,5,5)，$则$k=(3,-1,0)$或$(1,0,1)$

线性相关与线性无关

• 假设有一组向量$a_1,a_2,...a_m$
• 如果存在 不全为零 的数$k_1,k_2,...k_m$，使得$k_1{a}_1+k_2{a}_2+...+k_m{a}_m=0$，则$a_1,a_2,...,a_m$是线性相关，否则线性无关
• 线性相关的判定
  • 通过观察，利用定义即可判断
  • 太复杂了怎么办？
  • 定理一：向量组a1,a2,…,am线性相关的充要条件是a1,a2,…,am中至少有一个向量可由其余m-1个向量线性表示
  • 例：a1=(1,1,1,1) a2=(0,2,1,3) a3=(2,4,3,5) 是否线性相关？是。因为a1*2+a2=a3，由定理一可知，a1,a2,a3线性相关
  • 常用结论：含有零向量的向量组一定线性相关。单位向量组线性无关。单位向量是模等于1的向量

矩阵的秩

• 定义2：一个向量组$A$的秩是$A$的线性无关的向量的个数

• $a_1=(1,1,1,1),a_2=(0,2,1,3),a_3=(2,4,3,5)$这个向量组的秩是多少？$a_3=2a_1+a2$，但是$a_1,a_2$线性无关，所以这个向量组的秩是2。怎么知道$a_1{a}_2$向量无关？？

• 定义3：如果把一个向量组看成一个矩阵，则向量组的秩就是矩阵的秩。

• 还是上面那个例题，现在转成矩阵：
  $$\begin{gathered} A=\left[1,0,2 \\ 1,2,4 \\ 1,1,3 \\ 1,3,5\right] \end{gathered}$$
  这个矩阵的秩和组成它的向量组的秩一样，都是2

矩阵的范数与迹

思考问题

如何度量两个向量的相似程度？

对于实数和复数，由于定义了它们的绝对值或模，这样我们就可以用这个度量来表示它们的大小（几何上就是长度），进而可以考察两个实数或复数的距离。

例1。复数$X=a+bi$的长度或模指的是$||x||=\sqrt{a^2+b^2}$

例2。n维欧氏空间中向量$x$的长度或模定义为$||X||=\sqrt{x_1^2+x_2^2+...+x_n^2}$

向量的范数

定义一 在一个n维线性空间V中，若对于任意向量$X\in M$

常用的向量范数

• 1-范数 $||X|{|}_1={\sum }_{i=1}^n|x_i|$即向量所有元素绝对值之和
• 2-范数$||X|{|}_2=\sqrt{{\sum }_{i=1}^n{x}_i^2}$又称欧氏范数
• $\infty$-范数$||X|{|}_n=max|x_i|$即取元素绝对值最大

求下列向量的各种常用范数$x=(1,-2,3{)}^T$

解：

$||x|{|}_1=|x_1|+|x_2|+|x_3|=6$

$||x|{|}_2=\sqrt{{\sum }_i^n|x_i{|}^2}=\sqrt{14}$

$||x|{|}_n={\max }_i^3|x_i|=3$

范数都是要求绝对值的

矩阵的范数

• 1-范数（也称列范数）$||A|{|}_1={\max }_j^n{\sum }_{i=1}^n|a_{ij}|$
• $\infty$-范数（也称行范数）$||A|{|}_{\infty }=ma{x}_i^n{\sum }_{j=1}^n|a_{ij}|$
• 2-范数 $||A|{|}_2=\sqrt{{\lambda }_{max}(A^{T}A)}$
• ${\lambda }_{max}(A^{T}A)$为$A^T$乘以$A$的特征值的绝对值的最大值

例，求矩阵$A$的各种常用范数
$$A=\left[\begin{array}{ccc}1& 2& 0\\ -1& 2& -1\\ 0& 1& 1\end{array}\right]$$

范数有什么用？

范数是衡量向量和矩阵的距离，和它们的相似度，在机器学习的分类问题当中，如何判断两个特性向量和矩阵的相似性？

迹

定义3 在线性代数中，一个$n\ast n$矩阵$A$的主对角线（从左上方至右下方的对角线）上各个元素的总和被称为矩阵$A$的迹（或迹数），一般记住$tr(A)$.只有方阵才有迹

矩阵变换和矩阵分解

线性变换及其矩阵表示

定义1 $n$个变量$x_1,x_2,...,x_n$与$m$个变量$y_1,y_2,...,y_m$之间的关系

特征值、特征向量

定义2 设$A$是$n$阶矩阵，若存在数$\lambda$和非零向量$x$，使得$Ax=\lambda x(x̸=0)$，则称$\lambda$是$A$的一个特征值，$X$为$A$的对应特征值$\lambda$的特征向量。（$x$为非零向量）

特征值的性质

若$\lambda$ 是$A$的特征值，即$Ax=\lambda x(x̸=0)$，则：

• $k\lambda$是$kA$的特征值(k是常数)，且$kAx=k\lambda x$
• ${\lambda }^m$是$A^m$的特征值(m为正整数)，且$A^{m}x={\lambda }^{m}x$
• 若$A$可逆，则${\lambda }^{-1}$是$A^{-1}$的特征值，且$A^{-1}x={\lambda }^{-1}Ax$，${\lambda }^{-1}|A|$是$A^{\ast }$的特征值，且$A^{\ast }x={\lambda }^{-1}|A|x$
• $\phi (x)$是$x$的多项式，则$\phi (\lambda )是\phi (A)$的特征值，且$\phi (A)x=\phi (\lambda )x$
• 矩阵$A$和$A^T$的特征值相同，特征多项式相同。

特征值和特征向量的求法

$Ax=\lambda x$可以改写为$(A-\lambda I)x=0$

这实际上是一个$n$个未知数$n$个方程的齐次线性方程组，特征向量可看成是它的一个非零解。而此齐次线性方程组有非零解的充要条件是$|A-\lambda I|=0$（行列式，不是绝对值和模）,即：
$$\left|\begin{array}{cccc}{a}_{11}-\lambda & a_{12}& ...& a_{1n}\\ a_{22}& a_{22}-\lambda & ...& a_{2n}\\ ...& ...& ...& ...\\ a_{n1}& a_{n2}& ...& a_{nn}-\lambda \end{array}\right|=0$$
称为矩阵$A$的特征方程

从$A$的特征方程中解出的$\lambda$的值就是$A$的特征值。然后通过求解方程组$(A-\lambda Ix=0)$，就可以求出$A$的特征向量。

特征值和特征向量在机器学习中的应用

• 主成分分析
• 流行学习
• LDA
• 线性判别和其他算法都会用到特征向量的理论和方法

测试：

$$\{\begin{array}{ll}{y}_1=a_1{b}_1& \\ y_2=a_2{b}_2& \\ y_n=a_n{b}_n& \chi \end{array}$$

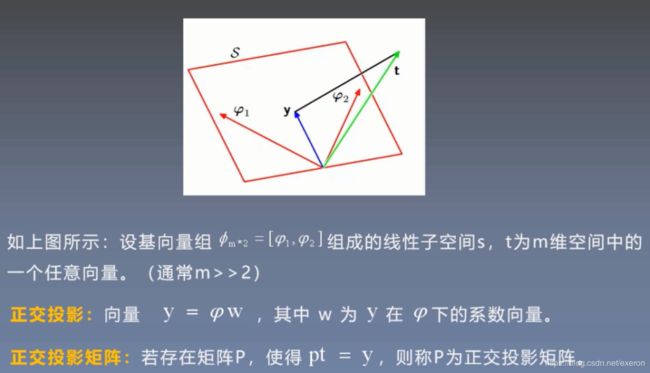
正交投影

概念：在线性代数和泛函分析中，投影是从向量空间映射到自身的一种线性变换。具体来说，正交投影是指像空间$U$和零空间$W$相互正交子空间的投影。

从解方程角度看，$Ax=b$可能无解，因为对任意的$x$，$Ax$总是在$A$的列子空间里，若向量$b$不在列空间里，则方程无解。但是我们可以将$b$利用正交投影矩阵投影到$A$的列子空间里得到正交投影$y$，然后求解$Ax=y$，寻找一个最佳近似解$x$。

二次型

则多项式可以写为：

$f(x_1,x_2,...,x_n)=X^{T}AX$ 该多项式是$n$元二次型，该多项式也为二次型的矩阵形式

二次型补充知识点

二次型经过变换，可以写成平方和形式：

$d_1{y}_1^2+d_2{y}_2^2+...+d_n{y}_n^2$

称为多项式一个标准型

注：

• 任意二次型的标准型是存在的
• 可应用配方法得到二次型的标准型

矩阵分解（QR分解，SVD奇异值分解）

定理1 设非奇异矩阵$A\in R^{n\ast n}$，则一定存在正交矩阵$Q$，上三角矩阵$R$，使得：$A=QR$

且当$R$的主对角元素均为正数时，该分解式是唯一的。

注：正交矩阵是$Q{Q}^T=E，E$为单位矩阵

奇异矩阵是行列式等于0的矩阵，非奇异矩阵是行列式不等于0的矩阵。

正交矩阵

QR分解是PCA的基础？

SVD奇异值分解