牛客网练习题
222.音乐研究:
解题思路:
首先,必须要使用到第一段得全部数据而且还是连续,这样我们就只要找到第二段中得第一个数,后面就是循环相减找到最小即可
代码:
#include
#include
#include
#include
#include
#define INT_MAX 2147483647
#define INT_MIN (-INT_MAX - 1)
using namespace std;
const int maxn=1003;
int a[maxn],b[maxn];
int main() {
int m,n;
while(cin>>n) {
long long res=INT_MAX; //必须要在循环时,重置为初始值
for(int i=0;i>a[i];
}
cin>>m;
for(int i=0;i>b[i];
}
int temp=0;
for(int i=0;itemp) {
res=temp;
}
temp=0;
}
cout< 总结:
想通逻辑后代码不难,在循环输入时和在计算最小res值得时候需要注意要重置得数:res得初始值INT_MAX和temp=0。
223.锦标赛
解题思路:
一开始我想到得思路是遍历数组每两个数为一组来对比,直到全部数都比较完或者选手输掉。但是貌似没有必要知道每一轮得比赛结果,题目需要求得是最多能存活几轮,所以即找到选手能战胜得全部对手,这样就可以找到最多得轮次了。
代码:
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxn=pow(2,20)+1;
int a[maxn];
int main() {
int a,b;
int x=1,n;
cin>>n;
cin>>a;
for(int i=1;i>b;
if(a>=b) x++;
}
int res=0;
while(x/2) {
x/=2;
res++;
}
cout< 总结:
这里很容易搞混题目得意思,不是找到输入顺序得最大轮次,而是找到这些积分中小美得最多轮次。还有就是没有必要知道每一轮得比赛结果,只要关心小美的参赛结果即可
253:子串:
解题思路:
使用函数创建出s(n,k)的总串,再使用kmp方式找子串。
创建总串:
先用x1记录n在k1进制中的最后一位是什么,然后n/k1来获取倒数第二位,以此类推,最后再倒序存进str1中以完成n在k1进制中的总串
后面就是kmp方式的getNext函数和kmp函数。
代码:
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,k;
char ss[16]= {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
char x1[1000005],t[1000005],Next[1000005];
string str;
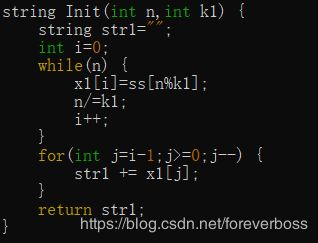
string Init(int n,int k1) {
string str1="";
int i=0;
while(n) {
x1[i]=ss[n%k1];
n/=k1;
i++;
}
for(int j=i-1;j>=0;j--) {
str1 += x1[j];
}
return str1;
}
void getNext() {
int i=0,j=-1,len=strlen(t);
while(i=1) return 1;
return 0;
}
int main() {
cin>>n>>t;
Next[0]=-1;
getNext();
for(int k=2;k<=16;k++) {
str="";
for(int i=1;i<=n;i++) {
str += Init(i,k);
}
int ans=kmp();
if(ans==1) {
cout<<"yes";
return 0;
}
}
cout<<"no";
return 0;
} 总结:
这个题目的总思路很简单,就是找到总串然后寻找子串是否存在,问题是如何计算出总串和灵活的使用kmp寻子串方法。这个可以当成kmp的进阶题目。
583.年轮广场:
解题思路:
首先找到位置到集结点的计算方法,然后计算每个地方设为集结点的结果,最后就是寻找最小值
代码:
#include
#include
#include
using namespace std;
const int maxn=1005;
int a[maxn];
#define INT_MAX 2147483647
#define INT_MIN (-INT_MAX - 1)
int main() {
int n,m,maxtemp=0,res=INT_MAX;
while(cin>>n>>m) {
for(int i=0;i>a[i];
}
sort(a,a+m);
for(int i=1;i<=n;i++) {
int d1=0;
for(int j=0;ji) {
maxtemp=min((a[j]-i),(n+i-a[j]));
}
if(d1d1) {
res=d1;
}
}
cout< 总结:
- 首先要确定集结地点,因为n的最大值只要1000,所以直接使用for循环来遍历计算寻找即可,不用考虑太多的优化技巧。
- 然后每确定一个集结点就要计算两个方向(顺序和逆序),而已还要看集结点和自己的位置在左边还是右边(即比较大小),在哪边会影响到计算方法。
- 最后就是计算方法,这个是纯数学问题了。
- 注意的是,这个是同步起步,而已是寻找最少时间,所以在计算每步的结果是要找的是最大值(即代码中的d1与maxtemp),计算结果时找的时最小值(即代码中的res与d1)。
- 记得还要初始化数据
224.送外卖
解题思路:
使用dfs递归法,一般得递归逻辑,先判断跳出递归得条件,然后找到递归方法得实现逻辑,再是返回上一步得函数参数设置,最后则是返回得类型结果。
代码:
#include
using namespace std;
typedef long long LL;
const int maxn=100005;
int a[maxn],b[maxn];
int visited[maxn],huan[maxn];
int flag=0,n;
char res[maxn];
bool dfs(LL pos,LL cur) {
if(pos<1 || pos>n) return false; //结束条件1
if(pos==n) { //结束条件2
res[cur]='\0';flag=1;return true;
}
if(visited[pos]==1) return false; //结束条件3
else if(visited[pos]==2) { //结束条件4
huan[pos]=1; return false;
}
visited[pos]=2; //实现逻辑
res[cur]='a';
if(dfs(pos+a[pos],cur+1)) {
if(huan[pos]) flag=2;
return true;
}
res[cur]='b';
if(dfs(pos+b[pos],cur+1)) {
if(huan[pos]) flag=2;
return true;
}
visited[pos]--;
return false; //最终返回得结果
}
int main() {
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++) cin>>b[i];
dfs(1,0);
if(flag==0) {
cout<<"No solution!"< 总结:
- 这题使用得终点不是n-1,而是n。就是导致我们不会使用a[0]这个值,所以dfs(1,0)开始。
- 这里得结束条件有4个:
- 走完的步数小于1或者大于n,不符合题意
- 走完的步数等于n,表示能在有限步数内走完,即输出res情况
- 返回已经走过的位置,且已经没有路可以走了
- 返回到已经走过的位置且是一个死循环(即不是字符串无限情况)
- visited[pos]的值:
- 值为2:初始值,若最终值也为2,说明走下一步符合题意,若huan[pos]!=0说明不是无限步数路线
- 值为1:说明走下一步不符合题意(即是结束条件1或者3)、
- 注意输出格式,需要完全符合题目中的输出格式
584.日历中的数字
解题思路:
题意:这题中的每个不同的日期中的年月日中出现的数字都算1次,即2077-04-03和2077-04-04中2的出现了2次,0出现了6次,7出现了4次
根据题意,我们就是计算年月日中的每个位数是否出现了x,然后再全部加起来即可。
代码:
#include
#include 总结:
这个题目看懂题意以后就简单很多,就是一个计算位数的出现次数的问题。这里注意的是每个单月和单日前面都会添加一个0,所以在计算0的时候记得添加判定条件。
585:安卓图案解锁:
解题思路:
这题的思路不是对输入的数值进行入手,而是对输入数字的索引值进行入手。如果索引值已经被访问过或者两个访问数中有数但是还是没有访问的状态既是错误输入格式。
代码:
#include
#include
#include
using namespace std;
int i,j,t,visedi,visedj,flag,p[3][3];
char s[35];
int main() {
while(cin>>s) {
memset(p,0,sizeof p);
for(t=0,flag=1,visedi=visedj=-1;s[t]&&flag;t++) {
int num=s[t]-'1';
i=num/3;
j=num%3;
if(visedi!=-1) {
if(p[i][j]==1) flag=0;
if((i+visedi)%2==0 && (j+visedj)%2==0 &&p[(i+visedi)/2][(j+visedj)/2]==0) {
flag=0; //i+visedi%2==0表示两个不是相隔的两个数字,例如0,1和1,2都是相隔的两个数字索引值,第三个判断是相隔的数是否已经被访问过了,如果没有既是错误输入
}
}
p[i][j]=1;
visedi=i;
visedj=j;
}
if(flag) cout<<"YES"< 总结:
这题的第一思路是对数值进行判断,但是对索引值的入手是个很好的方法。我们相隔两个没有访问过的数肯定是合法的,如果不是相隔的但是中间数已经访问过了那也是合法的。这个思路很巧妙,需要一点时间来想通。