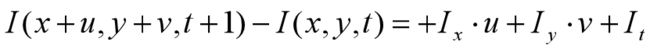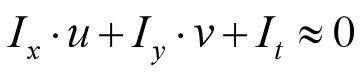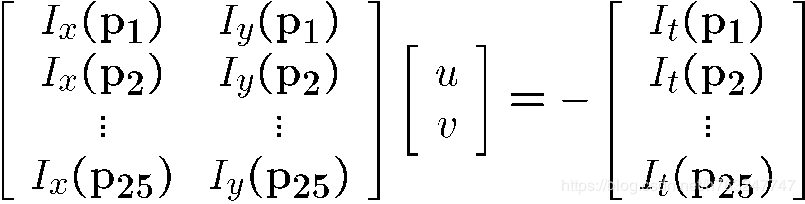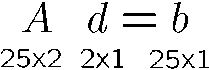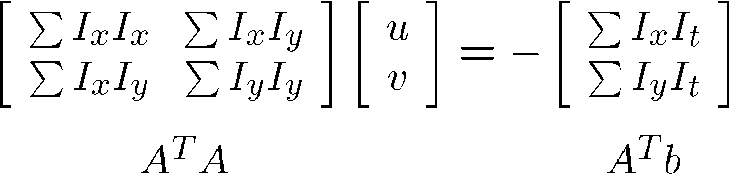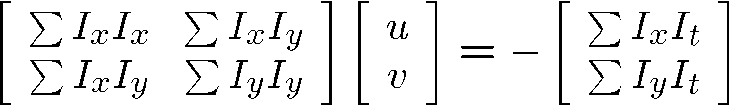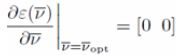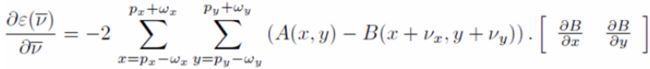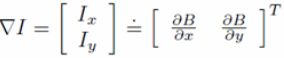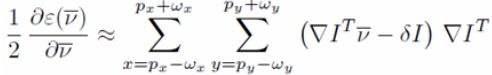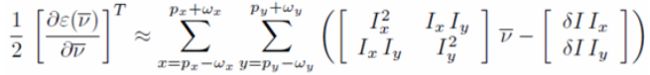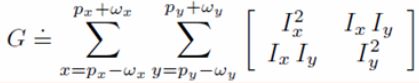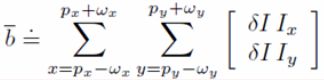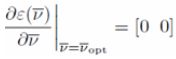光流（Optical Flow）
1 相关概念
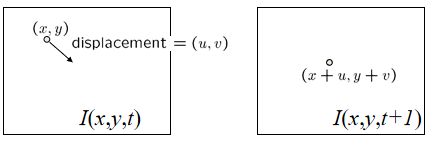
光流（场）：表示空间运动的物体在观察成像平面上的像素运动。
如下图所示，为了从第一个子图转移到第二个子图，
图像中每个像素点的运动如右子图所示。
运动场：物体在真实世界中的运动。
2 如何计算光流(Lucas-Kanade 算法）
2.1 亮度恒常性约束
已知连续的两帧图像，如上图所示，求解光流。
为了简化问题，在求解之前假设：
- 亮度恒常性：同一点在每一帧中的投影看起来都是一样的
- 小运动：点不会移动太远
- 空间一致性：点像它们的邻居一样移动
由第一条假设：亮度恒定
等式右边用泰勒公式展开：
所以：
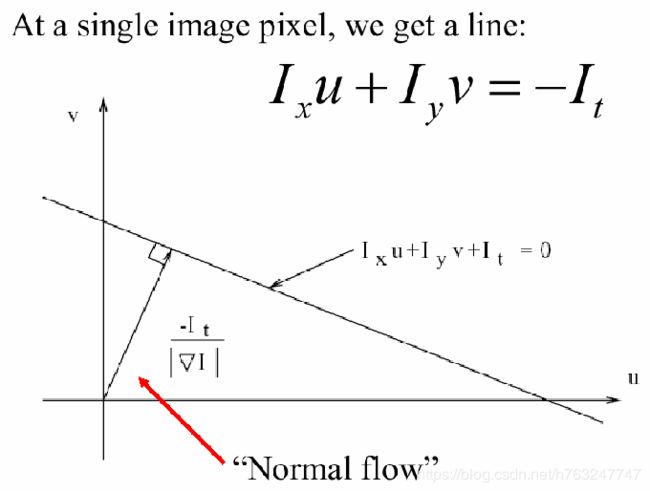
对于一个像素点，只有一个公式，两个未知数（u, v），无法求解。
但是从公式可以知道，运动垂直于亮度的梯度
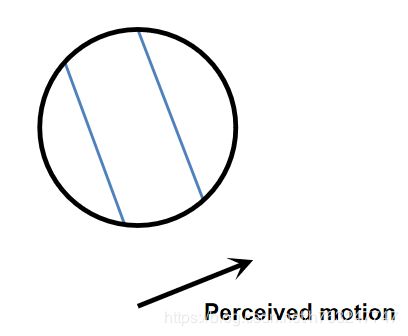
2.2 孔穴问题（aperture problem）
如上图所示，孔穴后面的一条直线沿右下方向移动，通过孔穴观察到的运动为左上方向
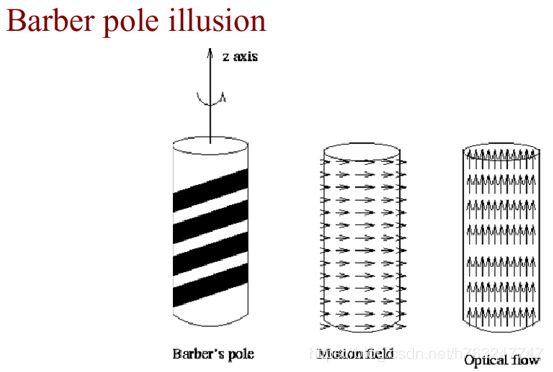
还有 barber pole 错觉，如下图所示：
圆柱体旋转，通过孔穴观察到的运动方向为上下
2.3 空间一致性约束（Spatial coherence constraint）
假设该像素点四周的像素点有相同的位移（u,v）
如果选择5*5 的窗口，这样每一个像素点有25个公式：
用矩阵的形式表示：
简化表示：
两边同时乘以A的转置：
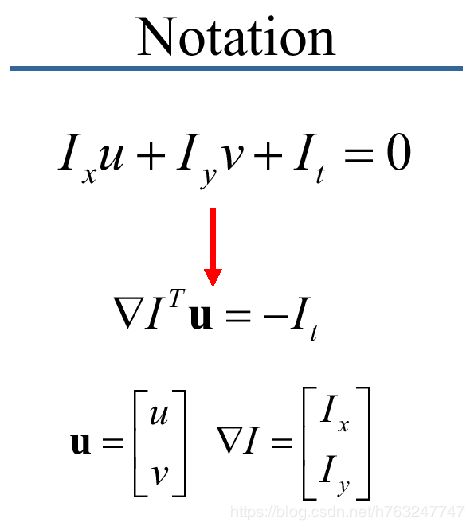
即：
这个公式被称为Lucas-Kanade equation。
上式左边矩阵即是Harris corner detector 的H矩阵，
要想使上式存在解，则：
可逆
的特征值不能太小（不能是一个平面，即low texture region）
的特征值不能一个太大，一个太小（不能是一个边，避免孔穴问题）
3 位移大的求解
在第二章，为了简化运算，设置了一个前提条件，运动的位移小。
如果这一条件不满足呢？这里引入LK光流的迭代算法
- 初始化，(x’,y’) = (x,y)
- 计算（u,v）根据Lucas-Kanade公式：
其中：
- 移动窗口，位移大小为（u，v）,即另x’=x’+u; y’=y’+v
- 计算
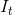
- 重复上面的过程直到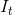的值很小
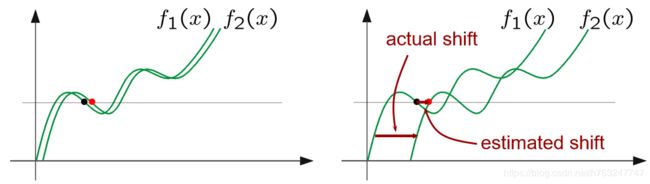
此算法有一个问题：容易混淆，如下图所示：
上方右图中，计算的值和实际值不一样。
4 Iterative Lukas-Kanade Algorithm
对于不满足2.1中三个条件，可以使用Iterative Lukas-Kanade Algorithm提高求解精度。
其步骤如下：
- 通过求解Lucas-Kanade方程估计每个像素处的速度（这里假设满足三个条件）
- 使用估计的流场，对I(t-1)进行变换，求变换后的图像与图像I(t)的光流
- 重复以上步骤,直到收敛
5 基于金字塔的LK光流算法
在第二章，为了简化运算，设置了三个前提条件，如果这三个前提条件不再满足，即：
- 亮度恒常性不满足
- 运动的位移不小
- 邻点的运动位移与中心像素点不一样
5.1 思路
当物体的运动速度很快时，两帧之间物体的运动位移很大，为了减小运动的位移，缩小图像的尺寸。
假设图像为400*400，物体的位移为16*16,
当图像缩小为200*200时，物体的位移为8*8，
当图像缩小到100*100时，物体的位移为4*4，
缩小后LK光流法又变得可以使用了。
5.2 具体步骤
4.2.1 对每一张建议一个高斯金字塔，最顶层为最低分辨率图像，最底层为原始图像（分辨率最高）
4.2.2 计算光流
- 最顶层图像的光流估计值为0，即
- 上一层的光流计算结果反馈到下一层，作为该层初始光流值：
其中 d 可以理解为特征窗口的位移，g 为光流值（物体的像素点的位移）。如下图所示，黑色方块表示邻域窗口，黄色的方框代表物体，在图像金字塔的各层中，邻域窗口的大小是不变的。
如果原图中，邻域窗口的位移为d
则图像金字塔中每层的位移为
，这里默认每次图像尺寸缩为原来的一半。
- 对于每一层
， 根据上一层求得的该层的初始光流值，先对该层的左边图像进行变换，
再求取变换后的图像与右边的图像的光流值，这样就满足条件2（运动很小）了。
假设变换后的图像与右边的图像的光流值为：
这时，领域内所有像素点的匹配误差和记为：
其中，A，B为坐标处的灰度值。
为了使匹配误差和最小，在最优处，导数为0，即：
匹配误差和的导数为：
利用泰勒公式，展开
，这里为什么可以展开？
因为变换后的图像与右边的图像相比，物体的位移（即光流）很小了。
因此，匹配误差和的导数变为：
令：
代入原公式，可得：
定义：
所以：
因为：
所以：
所以该层更新的光流值为：
。
根据该值，求得下一层的初始光流值。重复 层的过程。
这样一层一层传递下来，就可以求得最后的光流了。
最终原图的光流值就是每一层的光流值的叠加。如下图所示：
