最短路:Floyd(弗洛伊德)算法理解,最短路径存储
博客内容有误欢迎指出!欢迎评论交流!
Floyd算法算法理解起来比较简单核心代码也只有5行,所以不要被吓到了!
算法思想:逐个顶点试探法。逐步试着在原直接路径中增加中间顶点,若加入中间点后路径变短,则修改之;否则,维持原值所有顶点试探完毕,算法结束。
求最短路径步骤
1、
使用一个n*n的邻接矩阵map存储图,令其对角线元素为0,若存在弧
要求两个顶点a,b之间的的最短路径,有两种可能,一种是a直接到b,另一种是通过其他顶点作为中间顶点中转到b,即a->k->b,当然中间节点可能不止一个,也许通过多个中间节点a->k1->k2->…->b到达b的路径更短,floyd算法的基本思想就是枚举每个顶点加入作为中间顶点,如果该顶点作为中间顶点后路径更短则修改map矩阵的值。
2、
当将顶点A加入作为中间顶点,对每两个点作为起始点和终点,尝试将A作为中间节点,考虑使用A作为中转点的路径是否会比两点直接到达更短,如果更短则修改该两点之间的距离。
for(int i = 0;i<3;i++)
for(int j = 0;j<3;j++)
{
if(map[i][j]>map[i][0]+map[0][j])
map[i][j] = map[i][0]+map[0][j];
}
因为map[2][1] > map[2][0]+map[0][1],所以map[2][1]=map[2][0]+map[0][1],即本来C不能直接到B,所以路径长度为无穷,但是加入A作为中间节点中转,使得C到B的路径长度变为7,比之前的路径短,所以修改map中对应的值表示找到了更短的路径。最后结果如下图:

3、
之后在考虑了顶点A作为中间节点的情况下,再对每两个顶点作为起始点和终点,尝试将B作为中间节点,考虑将B作为中转节点的路径是否会比两点直接到达更短,如果更短则修改该两点之间的距离。
//考虑A作为中间节点中转
for(int i = 0;i<3;i++)
for(int j = 0;j<3;j++)
{
if(map[i][j]>map[i][0]+map[0][j])//顶点为A,这里是0
map[i][j] = map[i][0]+map[0][j];
}
//以下代码为尝试将B作为中间节点中转
for(int i = 0;i<3;i++)
for(int j = 0;j<3;j++)
{
if(map[i][j]>map[i][1]+map[1][j])//顶点为B,这里是1
map[i][j] = map[i][1]+map[1][j];
}
因为对每两个顶点都会执行map[i][j] = map[i][j] >(map[i][1]+map[1][j])?(map[i][1]+map[1][j]):map[i][j]来判断将B加入作为中转节点后路径是否比直接到达短,可以看到map[0][2]>map[0][1]+map[1][2],所以最后结果如下:

4、
到这想必已经很清楚下一步应该怎么做了。考虑完A,B作为中间节点后,将C作为中间节点时,对所有点对执行map[i][j] = map[i][j] >(map[i][2]+map[2][j])?(map[i][2]+map[2][j]):map[i][j]即可。当一个图有更多的节点时也是如此,将每个点尝试作为中间节点。
所以floyd算法的核心思想为:逐步试着在原直接路径中增加中间顶点,若加入中间点后路径变短,则修改之;否则,维持原值所有顶点试探完毕,算法结束。
所以floyd算法可以写成:
//n为顶点数
for(int k = 0; k<n;k++){//k表示逐步尝试将每个点作为中间节点中转
for(int i = 0; i<n;i++){//i表示起始点
for(int j = 0;j<n;j++){//j表示终点
if(map[i][j]>map[i][k]+map[k][j]){
map[i][j] = map[i][k] + map[k][i];
}
}
}
}
可以看到floyd算法使用了三重循环,所以时间复杂度为O(n3),比dijkstra算法的复杂度O(n2)高,但是floyd算法思路更加简单,并且floyd算法可以在图中有负边权的情况下使用,但是floyd算法不能求含负权回路(回路权值之和为负)图中的最短路问题,因为带有负权回路的图没有最短路径,比如下图中求1号顶点到3号顶点的最短路,因为存在一个1号点到3号点权值为-1的回路,每次走一次1->2->3的环,路径长度减少1,所以这种图不存在最短路径。

5、
最后如果想存储从起始点到终点的具体路径,可以设置一个n*n的二维数组path,path[i][j]是Vi到Vj的最短路径上Vj前一顶点序号
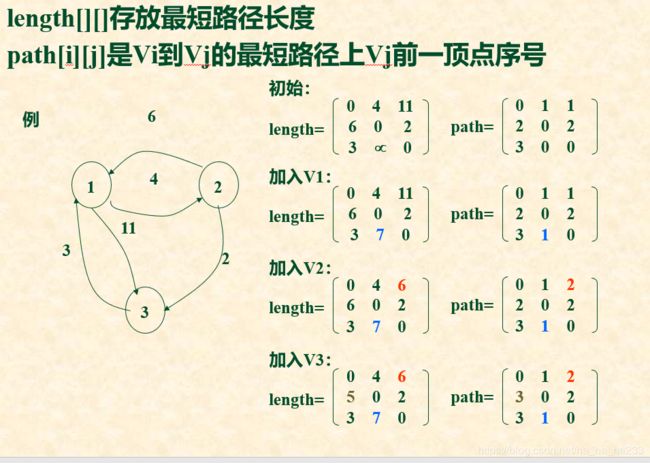
比如求点v3到点v2的最短路,由path[3][2] = 1,说明v3到v2最短路的前一个顶点是v1,然后再找从起点v3到v1的最短路path[3][1] = 3,可知v3到v1的最短路就是起点v3本身,只需要把上述逆序寻找的结果用栈保存下来,然后输出即可。
#include 输入:
3 5
1 2 4
1 3 11
2 1 6
2 3 2
3 1 3
参考:
https://www.cnblogs.com/ECJTUACM-873284962/p/6995648.html
https://www.cnblogs.com/lxt1105/p/6477639.html

