强化学习经典算法笔记(十)：使用粒子群算法训练Policy智能体

强化学习经典算法笔记(十)：使用粒子群算法训练Policy智能体

本文使用粒子群算法训练了一个小型Actor网络，共226个参数，完美解决了CartPole游戏。

粒子群算法实现

群体智能算法采用最简单的粒子群优化算法（PSO）。Python实现如下：

class PSO(object):
    def __init__(self, population_size, max_steps, dim=2, x_bound=[-10,10]):
        self.w = 0.6                            # 惯性权重
        self.c1 = self.c2 = 2
        self.population_size = population_size  # 粒子群数量
        self.dim = dim                            # 搜索空间的维度
        self.max_steps = max_steps              # 迭代次数
        self.x_bound = x_bound                # 解空间范围
        self.x = np.random.uniform(self.x_bound[0], self.x_bound[1],  # 也可以这样写：np.random.uniform([-1,10,20],[1,15,25],(3,3))
                                   (self.population_size, self.dim))  # 初始化粒子群位置
        self.v = np.random.rand(self.population_size, self.dim)       # 初始化粒子群速度
        fitness = self.calculate_fitness(self.x)
        self.p = self.x                         # 个体的最佳位置
        self.pg = self.x[np.argmin(fitness)]    # 全局最佳位置
        self.individual_best_fitness = fitness  # 个体的最优适应度
        self.global_best_fitness = np.min(fitness)  # 全局最佳适应度

    def calculate_fitness(self, x, value_net=None, device=None):
        return np.sum(pow((x-1),2), axis=1)
        # return value_net(torch.tensor(x).to(device))
        
    def evolve(self):
        # fig = plt.figure() # 费时
        for step in range(self.max_steps):
            r1 = np.random.rand(self.population_size, self.dim)
            r2 = np.random.rand(self.population_size, self.dim)
            # 更新速度和权重
            self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
            self.x = self.v + self.x
            # plt.clf()
            # plt.scatter(self.x[:, 0], self.x[:, 1], s=30, color='k')
            # plt.xlim(self.x_bound[0], self.x_bound[1])
            # plt.ylim(self.x_bound[0], self.x_bound[1])
            # plt.pause(0.0001)
            fitness = self.calculate_fitness(self.x)
            # 需要更新的个体
            update_id = np.greater(self.individual_best_fitness, fitness)
            self.p[update_id] = self.x[update_id]
            self.individual_best_fitness[update_id] = fitness[update_id]
            # 新一代出现了更小的fitness，所以更新全局最优fitness和位置
            if np.min(fitness) < self.global_best_fitness:
                self.pg = self.x[np.argmin(fitness)]
                self.global_best_fitness = np.min(fitness)
        print('best fitness: %.5f, mean fitness: %.5f' % (self.global_best_fitness, np.mean(fitness)))

    def evolve_step(self):
        r1 = np.random.rand(self.population_size, self.dim)
        r2 = np.random.rand(self.population_size, self.dim)
        # 更新速度和权重
        self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
        self.x = self.v + self.x
        fitness = self.calculate_fitness(self.x)
        # 需要更新的个体
        update_id = np.greater(self.individual_best_fitness, fitness)
        self.p[update_id] = self.x[update_id]
        self.individual_best_fitness[update_id] = fitness[update_id]
        # 新一代出现了更小的fitness，所以更新全局最优fitness和位置
        if np.min(fitness) < self.global_best_fitness:
            self.pg = self.x[np.argmin(fitness)]
            self.global_best_fitness = np.min(fitness)

Actor实现

Actor网络采用最简单的MLP，总共226个参数。

class Actor(nn.Module):
    def __init__(self,s_dim,hidden_size=32):
        super(Actor,self).__init__()
        # self.fc_s1 = nn.Linear(s_dim,hidden_size)
        # self.fc_a1 = nn.Linear(a_dim,hidden_size)
        # self.fc_Q1 = nn.Linear(num_atoms,hidden_size)
        
        self.fc = nn.Linear(s_dim, hidden_size)
        # self.fc_saq2 = nn.Linear(hidden_size,hidden_size)
        
        self.out = nn.Linear(hidden_size,2)
        
    def forward(self,st):
        st = F.relu(self.fc(st))
        # s_a_Q = F.relu(self.fc_saq2(s_a_Q))
        
        probs = F.softmax(self.out(st), dim=1) # accept or reject
        dist  = Categorical(probs=probs)
        action = dist.sample()
        a_probs = dist.probs.gather(-1,action.view(-1,1))
        return action, dist, a_probs

网络参数的转换

PSO对优化参数在形式上要求是一个向量，而Actor的参数是torch.tensor形式的张量，因此需要编写转换函数。

def get_vec_param(model):
    '''
    输出模型的参数，列向量形式
    '''
    keys = list(actor.state_dict().keys())
    param = []
    for key in keys:
        param.extend(actor.state_dict()[key].view(-1).numpy())
        print(key)
    return np.array(param)

def vec_param_reverse(model,params):
    '''
    将参数从列向量恢复成Tensor形式
    '''
    keys = list(actor.state_dict().keys())
    lens = [0]
    tmp = []
    for key in keys:
        lens.append(lens[-1]+len(actor.state_dict()[key].view(-1)))
    for i in range(len(lens)-1):
        tmp.append(params[lens[i]:lens[i+1]].reshape(actor.state_dict()[keys[i]].shape))
    return tmp

def param_update(model,params):
    '''
    用params更新model的参数
    params是Tensor的列表
    '''
    i = 0
    for param in model.parameters():
        param.data.copy_(torch.tensor(params[i]))
        i += 1

改写PSO

主要改动是计算粒子适应度的self.calculate_fitness()函数。对连续函数的优化可以通过numpy编写函数来实现，对于强化学习，fitness采用episode total reward作为fitness最为直接。因此calculate_fitness()函数的内部是一个rollout()函数，使Agent与环境完成一轮交互，得到total reward。

这里有进一步优化的空间。对粒子群的rollout()采用for循环来实现，也就是串行运行rollout()函数。在粒子群的平均游戏水平不断提高的过程中，rollout需要的总时间也在不断增加，甚至到无法接受的地步。

解决方案有两个，限制episode最大帧数；使用多线程技术，如multiprocessing。

class PSO(object):
    def __init__(self, population_size, max_steps, dim=226, x_bound=[-10,10]):
        self.w = 0.6                            # 惯性权重
        self.c1 = self.c2 = 1
        self.population_size = population_size  # 粒子群数量
        self.dim = dim                          # 搜索空间的维度
        self.max_steps = max_steps              # 迭代次数
        self.x_bound = x_bound                  # 解空间范围
        self.x = np.random.uniform(self.x_bound[0], self.x_bound[1],  # 也可以这样写：np.random.uniform([-1,10,20],[1,15,25],(3,3))
                                   (self.population_size, self.dim))  # 初始化粒子群位置
        self.v = np.random.rand(self.population_size, self.dim)       # 初始化粒子群速度
        fitness = self.calculate_fitness(self.x,actor)
        self.p = self.x                         # 个体的最佳位置
        self.pg = self.x[np.argmin(fitness)]    # 全局最佳位置
        self.individual_best_fitness = fitness  # 个体的最优适应度
        self.global_best_fitness = np.min(fitness)  # 全局最佳适应度
        
        
        # self.actor = Actor(self.env.observation_space.shape[0])
        
    def calculate_fitness(self, x ,actor):
        fitness = []
        for i in range(self.population_size):
            params = vec_param_reverse(actor,x[i])
            param_update(actor,params)
            reward = self.rollout(env,actor)
            fitness.append(-reward)
        return np.array(fitness)
        # return np.sum(pow((x-1),2), axis=1)
        # return value_net(torch.tensor(x).to(device))
    
    def rollout(self,env,actor,num_episode=2):
        total_r = []
        for episode in range(num_episode):
            st = env.reset()
            done = False
            reward = []
            while not done and len(reward)<=2000:
                at,dist,a_probs = actor(torch.FloatTensor(st).view(1,-1))
                st_,rt,done,_ = env.step(at.item())
                st = st_
                reward.append(rt)
            total_r.append(np.sum(reward))
        return np.mean(total_r)
    
    def evolve(self):
        # fig = plt.figure() # 费时
        for step in range(self.max_steps):
            r1 = np.random.rand(self.population_size, self.dim)
            r2 = np.random.rand(self.population_size, self.dim)
            # 更新速度和权重
            self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
            self.x = self.v + self.x
            # plt.clf()
            # plt.scatter(self.x[:, 0], self.x[:, 1], s=30, color='k')
            # plt.xlim(self.x_bound[0], self.x_bound[1])
            # plt.ylim(self.x_bound[0], self.x_bound[1])
            # plt.pause(0.0001)
            fitness = self.calculate_fitness(self.x,actor)
            # 需要更新的个体
            update_id = np.greater(self.individual_best_fitness, fitness)
            self.p[update_id] = self.x[update_id]
            self.individual_best_fitness[update_id] = fitness[update_id]
            # 新一代出现了更小的fitness，所以更新全局最优fitness和位置
            if np.min(fitness) < self.global_best_fitness:
                self.pg = self.x[np.argmin(fitness)]
                self.global_best_fitness = np.min(fitness)
        print('best fitness: %.5f, mean fitness: %.5f' % (self.global_best_fitness, np.mean(fitness)))

    def evolve_step(self):
        r1 = np.random.rand(self.population_size, self.dim)
        r2 = np.random.rand(self.population_size, self.dim)
        # 更新速度和权重
        self.v = self.w*self.v+self.c1*r1*(self.p-self.x)+self.c2*r2*(self.pg-self.x)
        self.x = self.v + self.x
        fitness = self.calculate_fitness(self.x,actor)
        # 需要更新的个体
        update_id = np.greater(self.individual_best_fitness, fitness)
        self.p[update_id] = self.x[update_id]
        self.individual_best_fitness[update_id] = fitness[update_id]
        # 新一代出现了更小的fitness，所以更新全局最优fitness和位置
        if np.min(fitness) < self.global_best_fitness:
            self.pg = self.x[np.argmin(fitness)]
            self.global_best_fitness = np.min(fitness)
        print('best fitness: %.5f, mean fitness: %.5f' % (self.global_best_fitness, np.mean(fitness)))
        

训练

def test_PSO():
    pso = PSO(100, 50)
    t1 = time.time()
    for i in range(pso.max_steps):
        pso.evolve_step()
    t2 = time.time()
    print('best fitness: %.5f' % (pso.global_best_fitness))
    print((t2-t1)*1000,pso.pg)
    # plt.show()
test_PSO()

训练曲线，50episode，最大帧数2000。全局最优解似乎依赖参数初始化，与参数训练关系不大；全体平均水平依赖进化过程，$c_1$和$c_2$参数是影响平均水平的关键超参数之一。

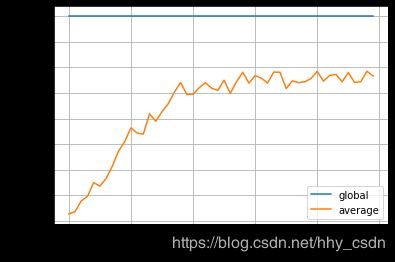
测试智能体水平

param = [ -6.87896184  , 5.31828134 ,  7.82629271 , 11.49515893 ,  1.0271663,
   7.80245951 ,  0.86431302  , 6.65732013 , -7.05834392 , -2.77873133,
   0.2737117  ,-11.41249693  ,-4.17671666 , 20.82454274 , 10.21621312,
   6.25155418 ,  6.84601883  ,-4.87639211  , 5.48519695,  -1.1041995,
  -1.27808745 ,  4.50248951  , 0.90334966 , -0.57488323 , -7.23400948,
   1.6727567  , -4.32737899  , 8.7040376  ,  1.26843809 , -3.85637248,
   5.37430959 ,  3.09935354  ,-2.00124693 ,  0.48069837 ,  6.6492788,
   4.11648383 , -1.59672105  ,-9.26551789  , 5.63647067 , -4.79751455,
  -1.28522267 ,  0.2746853   , 7.12620095  , 9.91123101  , 3.31125785,
  -0.98761396 ,  2.68209021  , 6.72879901 ,  2.17928962  , 0.43484967,
  -0.17051361 ,  7.18574405  ,-9.16824552 ,  6.85580742  , 0.39356039,
  -1.91960579 , -5.28012928  ,-6.64585406 , -2.88104786 , -0.93664817,
   4.62139195 ,  5.74788331  ,19.06988875 , 10.51456934 ,  7.28021944,
  -5.25869966 , 13.50789934   ,3.16167996 ,  2.1250155  ,  2.96896245,
  -5.15416997 ,  5.75334791   ,3.66229713 , 10.12652344 , -2.57011141,
 -20.84619964 ,  4.10380666  , 0.95247508 , -1.42566661,  -0.47485613,
   3.96775504 ,  4.72049171 ,  6.18003048 ,  9.31993689 , -2.15950689,
   3.97015033 , -7.20319404 , -2.86942767 , -1.21129762 , -9.40233665,
  -8.28052152 , -3.82436772 ,-11.51163202 , -6.73873155 ,-14.00143546,
   2.42079231 , 10.47531365  ,-9.64212868 ,  5.96629151, -10.68158861,
   0.46462626 ,  3.36130207  ,-9.50256154 ,  7.01769215,  -3.01207241,
  -7.82379394 , 11.10809385  , 5.47243914 ,  7.6781193 ,  -1.87116829,
   5.90623753 ,  5.61624662  ,-5.93666653 , -0.37315959 , 10.06546935,
  -8.92483729 ,  4.01005289  , 6.27772565 , -6.33809662 , -3.60532543,
  17.33469986 ,  1.76190327  ,-2.94241235 ,  1.61809649,  -5.57822847,
 -14.38582429 ,  2.03545268  ,-8.58136404 ,  5.07029378,   1.00060675,
  14.48148578 ,  7.69070164  , 2.18766084 ,  5.80161216 , -6.95092303,
  -2.524429   ,  6.21825582  , 8.88038541 , -1.4686213 ,   3.60089002,
   8.17486288 , -0.89304728  ,-0.70482453 ,  8.03158443 ,  8.69518794,
  -0.97965991 ,  3.51722298  , 6.46690211 ,  8.70787085 , -1.83222077,
   8.08140153 , -2.80639208  ,-0.72808167 , -3.83116559 ,  6.31652989,
  -5.77773393 ,  2.96048317  ,16.02955236 , -3.59239226, -11.55725956,
  -5.55743526 ,  3.73823912  ,-1.62886117 ,  1.80684061 , -4.94731609,
   6.39458554 , 10.81374966  , 6.53170828  ,-9.02887258 ,  4.61511603,
   4.45396772 ,  6.5356133   ,-9.79741849 ,  1.92043783 ,  0.94549931,
  -6.93996886 , -2.96215584  , 5.77684539 ,  2.5490333  ,  6.21542846,
  -1.23416605 , -4.91964363  , 0.80911777 , -6.10358595 ,  0.35812193,
  -5.35343233 , -0.96369554  ,-7.37074233 ,  0.6976975 ,   4.99837632,
   6.31696881 ,  3.4126433   ,-2.76266351 , 10.23040262 , -1.80379426,
   4.65767489  ,-4.49810261 ,  0.95758551 ,  5.79889708 ,  1.49071184,
  -7.61360839 ,  2.28477062,  -8.06971786 , -8.10108671 ,  5.73477901,
   2.52718578 , -0.33666324 , 17.12996485, -11.49077889 , -0.21451774,
  -5.13595118 , -6.2628335 ,   3.28553963 , -5.05751852 , -5.91102513,
   3.36703182 , -4.35517555 ,  4.82459182 , -7.18761084  , 4.47127266,
  17.14806542 ,  4.49706897  , 7.66597588 , 15.41274939 , 18.78789285,
  -7.43182869]
actor = Actor(4)
env = gym.make('CartPole-v1')
env = env.unwrapped
params = vec_param_reverse(actor,np.array(param))
param_update(actor,params)

for episode in range(10):
    st = env.reset()
    env.render()
    done = False
    reward = []
    while not done and len(reward)<=2000:
        at,dist,a_probs = actor(torch.FloatTensor(st).view(1,-1))
        st_,rt,done,_ = env.step(at.item())
        env.render()
        st = st_
        reward.append(rt)
    print(np.sum(reward))