动态规划算法问题(经典找零案例)
问题: 给定数组arr,arr中的所有的值都为正数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个整数aim代表要找的钱数,求换钱有多少种方法。
暴力搜索方法
思路分析
若给定arr={5, 10, 25, 1},aim=1000。
- 用0张5元的货币,让[10, 25, 1]组成剩下的1000元,最终方法数记作------res1;
- 用1张5元的货币,让[10, 25, 1]组成剩下的995元,最终方法数记作------res2;
- 用2张5元的货币,让[10, 25, 1]组成剩下的990元,最终方法数记作------res3;
- 用3张5元的货币,让[10, 25, 1]组成剩下的985元,最终方法数记作------res4;
- ……
- 用200张5元的货币,让[10, 25, 1]组成剩下的0元,最终方法数记作------res201;
则res1、res2……res201的累加和即为最终的结果。
具体实现
定义递归函数:int process1(arr, index, aim), 它的含义是如果用arr[index……N-1]这些面值的钱组成aim,返回总的方法数。
public static int coins1(int[] arr, int aim) {
long startTime = System.currentTimeMillis();
if (arr == null || arr.length == 0 || aim < 0) {
return 0;
}
int result = process1(arr,0,aim);
long endTime = System.currentTimeMillis();
System.out.println("暴力搜索方法所用时间:" + (endTime - startTime) +"ms");
return result;
}
public static int process1(int[] arr, int index, int aim) {
int res = 0;
// 判断是否所有面值的货币均已经计算完
if (index == arr.length) {
// 判断本次递归调用时钱的总数是否已经凑够,如果已经凑够则将总方法数加1
res = aim == 0 ? 1 : 0;
} else {
// 循环计算i张当前面值的货币
for (int i = 0; arr[index] * i <= aim; i++) {
// 递归调用当使用i张当前面值的货币时,用其它货币组成剩下的钱
res += process1(arr, index + 1, aim - arr[index] * i);
}
}
return res;
}
暴力搜索方法比较好理解,但他在计算中存在大量的重复递归过程。
例如已经使用了0张5元和1张10元货币的情况下,后续将求:process1(arr,2,990)
而当计算使用2张5元和0张10元时,后续同样需要求:process1(arr,2,990)
因此这种重复的递归运算将造成大量的时间浪费。
记忆搜索方法
思路分析
由于暴力搜索方法中存在大量的重复递归,因此我们可以使用一个“记忆库”用于存储已经计算过的值,在本题中,使用index货币组成剩下的aim钱的值是一一对应的,因此可以使用int mem[index][aim]数组表示记忆库,其元素值为可以组成的方法数。
具体实现
- 每计算完一个process(index,aim),都将结果放入mem中,index和aim组成共同的key,返回结果为value。
- 要进入一个递归过程时,先以index和aim组成的key在mem中进行查询,如果已经存在value,则直接使用,如果不存在,再进入递归过程。
public static int process2(int[] arr, int index, int aim, int[][] mem) {
int res = 0;
// 判断是否所有面值的货币均已经计算完
if (index == arr.length) {
// 判断本次递归调用时钱的总数是否已经凑够,如果已经凑够则将总方法数加1
res = aim == 0 ? 1 : 0;
} else {
int memVal = 0;
// 循环计算i张当前面值的货币
for (int i = 0; arr[index] * i <= aim; i++) {
// 获取记忆库中当使用i张index货币时,用其它货币组成剩下的钱
memVal = mem[index + 1][aim - arr[index] * i];
// 判断记忆库中存在记录
if (memVal != 0) {
// 将记忆库中的方法数累加到结果中
res += memVal == -1 ? 0 : memVal;
} else {
// 递归调用当使用i张当前面值的货币时,用其它货币组成剩下的钱
res += process2(arr, index + 1, aim - arr[index] * i, mem);
}
}
}
// 将使用index货币组成aim钱的结果存储到记忆库中
mem[index][aim] = res == 0 ? -1 : res;
return res;
}
动态规划方法
思路分析
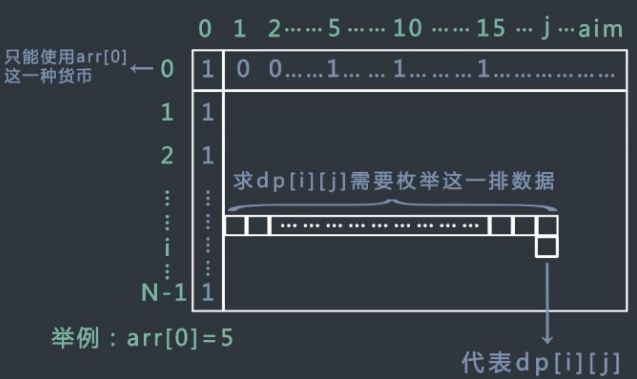
如果arr长度为N,生成行数为N,列数为aim+1的矩阵dp。
dp[i][j]的含义是在使用arr[0]...arr[i]货币的情况下,组成钱数j的方法数。
- 如果完全不用arr[i]货币,只使用arr[0]...arr[i-1]货币时,方法数为dp[i-1][j]。
- 如果用1张arr[i]货币,剩下的钱使用arr[0]...arr[i-1]货币组成,方法数为dp[i-1][j-1*arr[i]]。
- 如果用2张arr[i]货币,剩下的钱使用arr[0]...arr[i-1]货币组成,方法数为dp[i-1][j-1*arr[i]]。
- 如果用3张arr[i]货币,剩下的钱使用arr[0]...arr[i-1]货币组成,方法数为dp[i-1][j-1*arr[i]]。
- ……
dp[i][j]的值即为上述所有值得累加和。
求每一个位置都需要枚举,时间复杂度为O(aim)。dp一共有N*aim个位置,所以总的时间复杂度为O(N*aim2)
最终的结果值即为矩阵最右下角的dp[N-1][aim]。
记忆搜索方法与动态规划方法的联系
- 记忆化搜索方法就是某种形态的动态规划方法。
- 记忆化搜索不关心到达某一个递归路径的路程。只是单纯地堆计算过的递归过程进行记录,避免重复递归的过程。
- 动态规划方法则是规定好每一个递归霍城的计算顺序,一次进行计算,后面的计算过程严格依赖前面的计算过程。
- 两者都是空间换时间的方法,也有枚举的过程,区别在于动态规划规定计算顺序,而记忆搜索不用规定。
什么是动态规划方法
- 本质是利用申请的空间来记录每一个暴力搜索的计算过程,下次要用结果的时候直接使用,而不再进行重复的递归过程。
- 动态规划规定每一种递归状态的计算顺序,依次进行计算。从简单到复杂,按顺序计算。
具体实现
public static int process3(int[] arr, int aim) {
// 创建dp矩阵
int[][] dp = new int[arr.length][aim + 1];
for (int i = 0; i < dp.length; i++) {
dp[i][0] = 1; // 凑成0元的方法必然是什么货币都不用,只有1种
if (i == 0) {
// 如果只是用arr[0]这一种货币,则能凑到j钱置1
for (int j = 0; j < dp[i].length; j++) {
dp[i][j] = j % arr[i] == 0 ? 1 : 0;
}
} else {
for (int j = 1; j < dp[i].length; j++) {
int temp = 0;
// 枚举使用k张arr[i]货币后dp[i-1]中组成剩下钱数的方法数
for (int k = 0; k * arr[i] <= j; k++) {
temp += dp[i - 1][j - k * arr[i]];//方法数累加
}
dp[i][j] = temp;
}
}
}
// 返回dp矩阵最右下角的值即为最后结果
return dp[arr.length - 1][aim];
}
动态规划方法的再优化
思路分析
由于动态规划方法的执行顺序有着严格的规定,因此使得对算法的进一步优化成为可能。
对于刚才的问题中,我们需要枚举dp[i-1][j-k*arr[i]](k=1,2,3...)并与dp[i-1][j]累加,实际上dp[i-1][j-k*arr[i]](k=1,2,3...)的累加值就是dp[i][j-arr[i]]。
所以可以简化为:
dp[i][j] = dp[i][j-arr[i]] + dp[i-1][j]
从而彻底省略枚举过程。时间复杂度从O(N*aim2)变为O(N*aim)
具体实现
经过优化后的代码实现如下:
public static int process4(int[] arr, int aim) {
// 创建dp矩阵
int[][] dp = new int[arr.length][aim + 1];
for (int i = 0; i < dp.length; i++) {
dp[i][0] = 1; // 凑成0元的方法必然是什么货币都不用,只有1种
for (int j = 1; j < dp[i].length; j++) {
if (i == 0) {
dp[i][j] = j % arr[i] == 0 ? 1 : 0;
} else if(j >= arr[i]){
dp[i][j] = dp[i][j - arr[i]] + dp[i - 1][j];
} else {
dp[i][j] = dp[i - 1][j];
}
}
}
// 返回dp矩阵最右下角的值即为最后结果
return dp[arr.length - 1][aim];
}
动态规划方法的空间优化
我们可以看到,经过优化的动态规划方法速度已经非常让人满意,但是它的空间浪费却很严重,我们发现动态规划方法是严格的矩阵从上至下、从左至右的方向顺序计算,那么其实真正每次计算式只需要用到的是当前行与当前行的上一行,因此其实我们可以将原本的dp二维矩阵简化为一维向量。
通过读取和修改向量本身的元素值来达到目的,修改后的代码如下所示:
public static int process5(int[] arr, int aim) {
// 创建dp向量
int[] dp = new int[aim + 1];
for (int i = 0; i < arr.length; i++) {
dp[0] = 1; // 凑成0元的方法必然是什么货币都不用,只有1种
for (int j = 1; j < dp.length; j++) {
if (i == 0) {
dp[j] = j % arr[i] == 0 ? 1 : 0;
} else if(j >= arr[i]){
dp[j] += dp[j - arr[i]];
}
}
}
// 返回dp向量尾元素即最终结果
return dp[aim];
}
各种计算方法的运行速度对比
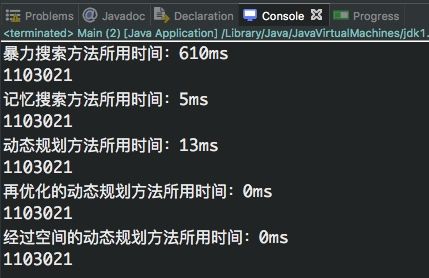
上述所有的实现代码中,都加入了记录算法开始时间和结束时间的代码,我们通过运行测试,得到下面的结果:
- 可以看到,暴力搜索方法毋庸置疑是速度最慢的,因为其存在大量的重复递归过程。
- 记忆化搜索方法由于避免了重复递归,因此效率更高一些。
- 经过优化的动态规划方法可以看到在我的实测环境中,运行时间近乎为0ms,可以说是非常快的。
暴力递归优化成动态规划方法的大体过程
- 实现暴力递归方法;
- 在暴力搜索方法的函数中看看哪些参数可以代表递归过程。
- 找到代表递归过程的参数之后,记忆化搜索方法的实现非常容易。
- 通过分析记忆化搜索的依赖路径,进而实现动态规划。
- 根据记忆化搜索方法改出动态规划方法,进而看看是否能够化简,如果能化简,还能实现时间复杂度更低的动态规划方法。
动态规划方法的关键点
- 最优化原理:也就是最优子结构性质。指一个最优化策略具有这样的性质,不论过去状态和决策如何,对前面的决策所形成的状态而言,余下的诸决策必须构成最优策略。简单来说就是一个最优化策略的子策略总是最优的,如果一个问题满足最优化原理,就成为其具有最优子结构性质。
- 无后效性:指某状态下决策的收益,只与状态和决策相关,与到达该状态的路径无关。
- 子问题的重叠性:动态规划将原来具有指数级时间复杂度的暴力搜索算法改进成了具有多项式时间复杂度的算法。其中的关键在于解决冗余,这是动态规划算法的根本目的。
本文为博主学习牛客网课程《直通BAT-面试算法精讲课》的学习笔记
如果需要购买该课程,可以使用博主的优惠码:Adg00aI,获取10元优惠。