机器学习---关于斗鱼直播人数的分析

1.需求分析
最近学习了爬虫，于是我爬取了4天内斗鱼直播人数（间隔为1小时）
2.所需要的库

numpy
scipy
matplotlib

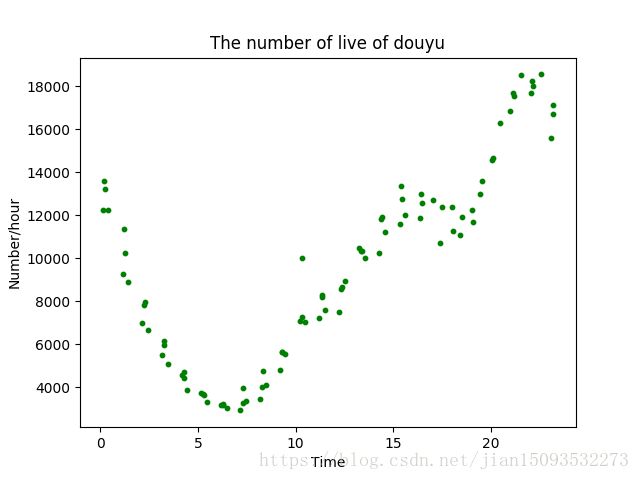
3.通过散点图观察斗鱼直播人数的变化趋势

# -*- coding:utf-8 -*-

from matplotlib import pyplot as plt
import numpy as np

# 获取数据
x,y = np.loadtxt('number.txt', unpack=True)

# 标题
plt.title('The number of live of douyu')
# 散点图的x轴
plt.xlabel('Time')
# 散点图的y轴
plt.ylabel('Number/hour')
# 绘制散点图
plt.scatter(x,y,s=10, c='g', marker = 'o')
plt.show()

结果图像为：

4.通过每天的子图分析斗鱼直播人数的变化趋势

import matplotlib.pyplot as plt
import scipy as sp

#　获取数据（获取到的是一个二维数组）
data = sp.genfromtxt('number.txt', delimiter='\t')
# 改变维度
data = data.reshape((4,46))

for x, c in enumerate('rgby'):
    plt.xlabel('Time')
    plt.ylabel('Number/hour')

    # 画出每天的子图
    # subplot(x,y,z)函数:
        # ｘ表示是图排成x行，
        # y表示图排成y列,
        # z表示图所在的位置，z=1表示从左到右从上到下的第一个位置。
    plt.subplot(4,1,x+1)

    # 填充数据
    for y in range(0,23):
        plt.scatter(data[x][y*2], data[x][y*2+1], c=c)

plt.show()

结果图像为：

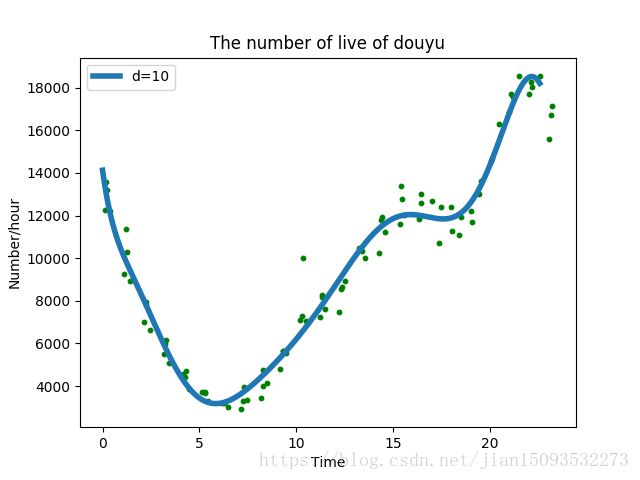
5.数据曲线拟合
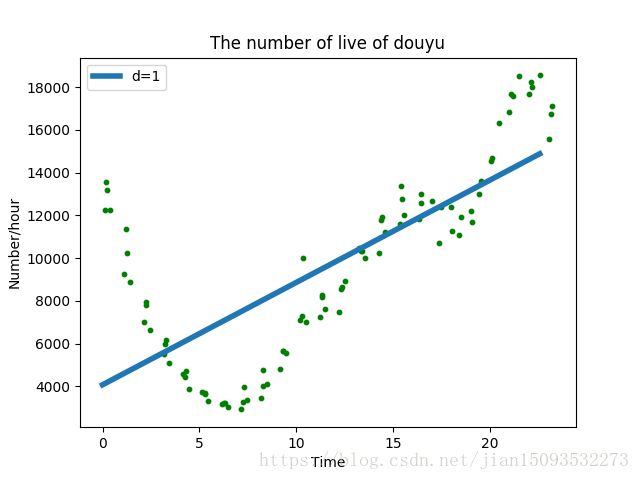
（１）一阶曲线拟合

import matplotlib.pyplot as plt
import scipy as sp

# 获取数据
data = sp.genfromtxt('number.txt', delimiter='\t')
x = data[:,0]
y = data[:,1]

# 误差函数
def error(f, x, y):
    return sp.sum((f(x)-y)**2)

# 进行曲线拟合
# polyfit(x,y,n)　多项式拟合函数
    # x，y为将要拟合的数据,n为多项式阶数

fp1, residuals, ranks, sv, rcond = sp.polyfit(x, y, 1, full=True)
# 多项式参数
print('Model parameters:%s' % fp1)
# 剩余误差
print('剩余误差为%s' % residuals)
# 矩阵的秩
print('秩为:%s' % ranks)
＃　奇异值
print('sv:%s' % sv)
# 数据合适的相对条件数，小于这个相对于最大奇异值的奇异值将被忽略
print('rcond:%s' % rcond)

# 封装多项式　
# poly1d() 封装多项式函数，以便进行多项式操作
f1 = sp.poly1d(fp1)
print(error(f1, x, y))

＃　画出函数f(x)
fx = sp.linspace(0, x[-1], 1000)
plt.plot(fx, f1(fx), linewidth=4)
plt.legend(['d=%i' % f1.order], loc='upper left')

# 标题
plt.title('The number of live of douyu')
# 散点图的x轴
plt.xlabel('Time')
# 散点图的y轴
plt.ylabel('Number/hour')
# 绘制散点图
plt.scatter(x,y,s=10, c='g', marker = 'o')
plt.show()

运行结果为:

Model parameters:[ 478.66300443 4075.36898904]
剩余误差为[8.8590773e+08]
秩为:2
sv:[1.36322927 0.37630568]
rcond:2.042810365310288e-14

结果图像为：

（２）二阶曲线拟合
运行结果为：

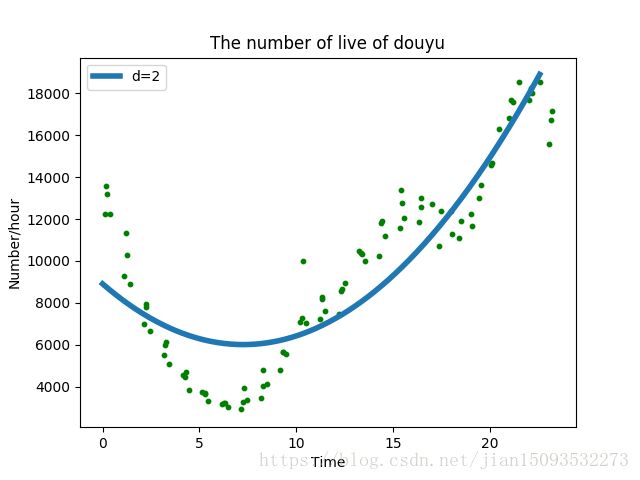
    Model parameters:[  54.9547582  -798.30744726 8907.0284263 ]
    剩余误差为[3.90059835e+08]
    秩为:3
    sv:[1.64639016 0.52810615 0.10248572]
    rcond:2.042810365310288e-14

结果图像为

（３）三阶曲线拟合
运行结果为：

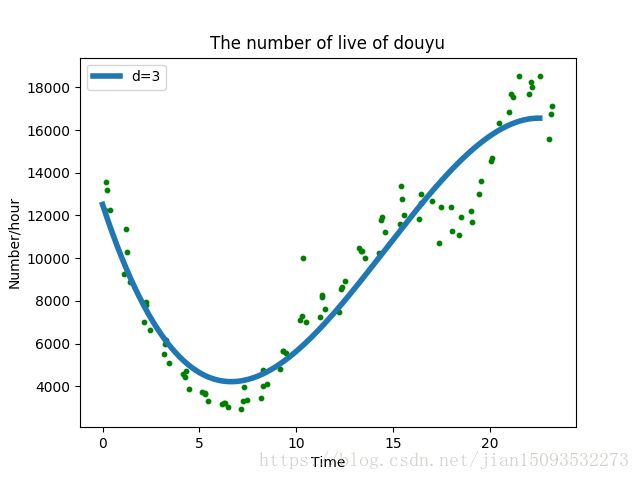
Model parameters:[-6.16018391e+00  2.69640433e+02 -2.76866270e+03  1.25151351e+04]
剩余误差为[1.67489264e+08]
秩为:4
sv:[1.88850751 0.63670046 0.16616374 0.02327085]
rcond:2.042810365310288e-14

结果图像为

（４）十阶曲线拟合
运行结果为：

Model parameters:[ 3.07048176e-06 -3.64875839e-04  1.83725579e-02 -5.11622610e-01
  8.62348312e+00 -9.03802702e+01  5.80724751e+02 -2.16746468e+03
  4.46070312e+03 -6.61013798e+03  1.41250814e+04]
剩余误差为[44746797.93457191]
秩为:11
sv:[3.10503917e+00 1.06624260e+00 4.45564899e-01 1.47411546e-01
 3.90076369e-02 8.70857106e-03 1.64513856e-03 2.56887566e-04
 3.24281639e-05 3.15878038e-06 2.05570899e-07]
rcond:2.042810365310288e-14

结果图像为

（５）五十三阶曲线拟合
运行结果为：

Model parameters:[-1.20186843e-59  5.92330089e-58  2.31073487e-57 -2.07105957e-55
 -5.39861117e-54 -3.87174670e-53  1.58958937e-51  6.85460636e-50
  1.37049630e-48  9.16075677e-48 -4.24500777e-46 -1.97071612e-44
 -4.61835201e-43 -5.58432877e-42  5.56531716e-41  5.11158341e-39
  1.53529320e-37  2.68074031e-36  1.03032711e-35 -1.14510044e-33
 -4.69493398e-32 -1.02314997e-30 -9.43658219e-30  2.54861622e-28
  1.42637691e-26  3.41515035e-25  3.26711659e-24 -8.96800836e-23
 -4.79644819e-21 -9.88041617e-20 -2.16695537e-19  5.14230636e-17
  1.57276614e-15  1.16287535e-14 -6.37920454e-13 -2.14621726e-11
 -6.14638113e-11  1.16790316e-08  2.03936521e-07 -4.89100839e-06
 -1.48855311e-04  3.04462752e-03  6.52561034e-02 -3.01057537e+00
  5.07423168e+01 -5.05704299e+02  3.30706840e+03 -1.46222132e+04
  4.35907921e+04 -8.53102218e+04  1.03985599e+05 -7.18148103e+04
  2.07357461e+04  1.10447516e+04]
剩余误差为[]
秩为:26
sv:[6.91873395e+00 2.18598063e+00 1.01791406e+00 5.06116914e-01
 2.24776404e-01 9.13037920e-02 3.53656185e-02 1.29920150e-02
 4.74255101e-03 1.63122663e-03 5.27053429e-04 1.61464902e-04
 4.87122326e-05 1.46024039e-05 4.12650488e-06 1.09052700e-06
 2.73611102e-07 6.62848211e-08 1.59479525e-08 3.91207721e-09
 9.60243315e-10 2.23629549e-10 5.04056647e-11 1.10367053e-11
 2.20996812e-12 4.20203572e-13 8.06280215e-14 2.41476940e-14
 2.92349454e-15 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 7.26904327e-16 7.26904327e-16 7.26904327e-16
 7.26904327e-16 4.44030790e-16]
rcond:2.042810365310288e-14

结果图像为

6.结论
由散点图和子图可知，斗鱼直播人数在晚上22点达到最高值，在早上６点的时候达到最低值。
数据的曲线拟合总图为