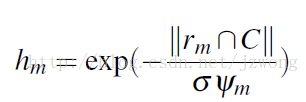Segmentation Driven Low-rank Matrix Recovery for Saliency Detection

发表在13年BMVC上的一篇文章，读完感觉写的挺好的，一个关键创新点是使用了背景与边界有较长的相交线这一先验知识。下面对这篇文章进行一下简单翻译与总结。才发现文章有些地方与我的思路有些相近啊！

简介

现有的视觉显著性检测模型主要分为两类：生物学模型的计算模型。生物学模型从边的方向、颜色、光照等特征中寻求视觉显著性，通常是基于特征集合上的中央-四周不同的框架。生物学模型的目标是找一些最能抓住人注意力的点，得到的显著性图往往是稀疏模糊的。相反，计算模型则多受生物学模型的启发，力图从周围区域中找到突出的物体。有大量的基于全局、局部和区域对比的不同形式的计算模型，比如说信息论、图模型、学习模型、统计模型、频率域分析等。一般来说，这些模型对简单一致场景下的物体能实现很好的显著性检测，因此所提出的算法往往也只在像MSRA-1000这种相对简单的数据集上进行验证。然而，对于混杂背景或者背景与物体对比度较低的复杂背景下，这些模型的鲁棒性并不好。基于上述问题，该文提出了一个无监督的低秩矩阵复原模型用于显著性检测。一个关键点是提出了一个自底向上的先验知识来约束图像特征，从而使之能更好地符合低秩矩阵复原模型。为了达到这个目的，提出了一个叫做“分割先验”的东东。传统上，显著性用来指导物体分割，在这里提出的方法恰恰相反，利用分割来指导显著性检测。

综述

图1是所提出的分割驱动的低秩矩阵复原模型的框架。一个输入图像首先进行三个层次的分割：细粒度的，中粒度的和粗粒度的。细粒度的分割将输入图像分割成大量的超像素，中粒度的分割同样过分割图像，但是希望产生的区域尽可能少，而粗粒度的最大程度上将物体从背景中分割出来，因此图像可能过分割或者欠分割。基于这三个层次的分割从超像素中提取图像特征，从中粒度和粗粒度分割中得到分割先验。然后低秩复原模型被用来生成初步的显著性图。最后，最初的显著性图通过使用中粒度分割先验来平滑产生最优的显著性图。

低秩矩阵复原模型

这一部分是老生常谈，没有作者创新的地方，就是单单阐述了一下别人提出的模型。基本思路：提取特征构建特征矩阵->低秩稀疏矩阵分解->稀疏矩阵求列显著性值->阈值判断显著性与否，具体不再多言。

带有分割先验的低秩矩阵复原模型

直接将低秩矩阵复原模型应用在显著性检测问题中是基于背景同质性且与物体有较大对比的假设之上。然而现实中，很多背景是杂乱的且物体很可能与背景的一部分比较相近。为了提高显著性检测的鲁棒性，一种可行的方式就是采取一种高层的先验来修正输入特征从而使得特征矩阵具有低秩性。“修正”潜在的想法就是赋予那些很可能是背景的超像素对应的特征向量小的权重，给很可能是物体的超像素对应的特征向量大的权重。

对于显著性检测而言提出了很多先验，比如说中心先验，颜色先验等，这些先验的主要缺点是适用性差。比如说，中心先验假设物体总是出现在图像的中心位置，颜色先验假设物体总是暖色调。显然这样的假设在现实中并不总是成立。在这篇文章中，作者提出了一个自底向上的分割先验。如下图：

首先看一下输入图像及它们的粗分割。显著物体位于图像的各个位置，中心，上不，左右，角落等。背景和物体同时都被分割成了几个部分，因此不能期待自底向上的分割彻底地将物体从背景中分割出来。然而，由背景分割开产生的区域有很大的可能性与图像的边界相连，而物体分割产生的区域则很少能与边界相连。即使物体在边界上被截断，像最右边两幅图像中的自行车和孩子，比起整个显著性物体而言边界区域还是较小的。相反，背景的边界区域通常则很大，因为背景往往表现地更加均匀统一，像天空、马路等。这个现象启发我们物体能够通过自底向上的分割从背景中粗略地分割出来。因此，我们根据每个分割区域与图像边界的连接性提出了分割先验：

具体符号解释见论文，基本思想就是给那些与图像边界相接触的区域（很可能是背景）小的权重，而给显著性物体大的权重。

注意在上图中可以看到，仍然有一些背景区域并不与图像边界相连，同时有一些显著性物体不可避免地与背景融合到了一起。事实上，我们上面提出的分割先验并不能完美地将物体从背景中分割出来，然而从粗粒度中得到的分割先验的确能指导低秩复原模型来处理显著性检测的任务。（后面这一点感觉作者可能存在错误，文章图1的逻辑并非如此）这时候的输入矩阵就变成了由 细粒度分割得到的特征矩阵与 粗粒度分割得到的分割先验矩阵对应位置的乘积矩阵：

将矩阵B输入到低秩矩阵复原模型中，求解得到稀疏矩阵E，显著性物体在稀疏矩阵E中被强调出来。

后平滑

由低秩复原模型得到的显著性图仍可能包含某些噪声：背景中出现某些较大的显著性值或者物体中某些显著性值较小。主要由两方面原因导致这个现象：一方面，背景的超像素在特征域上可能与物体有较高的相似性；另一方面，矩阵低秩复原模型分解矩阵的时候并没有考虑到空间信息。为了移除噪声，最初得到的显著性图在细粒度和中粒度上进行平滑（ 记住这个平滑方式，比我的平滑高明多了！）

在细粒度上考虑上面的模型。显然，位于当前超像素周围且与当前超像素表现较为相近的超像素对计算显著性贡献较大，反之则相反。因此，细粒度下的平滑保证当前超像素与其邻居在显著性上的一致性。

细粒度的平滑可能还不够。令S',Hm,R分别表示细粒度平滑后得到的显著性图，中粒度的分割先验和中粒度分割产生的分割图，

意思是说最后再在像素级别上平均一下得到最终的显著性图。

实验结果很不错，论文到这里基本上就完

注：我查了一下，论文作者现就职于深圳大学，该文纯属本人对论文的理解，有任何问题可发邮件至 jzwangATbjtuDOTeduDOTcn 讨论交流。记于2017年1月1日。