ResNet(残差网络)几个关键问题的理解
一、ResNet概述
开篇首先来膜拜下大神何恺明,大神获得博士学位后于2011年加入微软亚洲研究院(MSRA)工作。2016年,加入Facebook AI Research(FAIR)担任研究科学家,研究方向和兴趣是计算机视觉和深度学习。大神在2018年荣获PAMI青年研究员奖、2009年获CVPR 2009、CVPR 2016最佳论文奖、2016年获CVPR、2017年ICCV (Marr奖)、2017年ICCV最佳学生论文奖、2018年ECCV最佳论文荣誉奖。他的关于深度残差网络(ResNets)的论文是在谷歌Scholar Metrics 2018年所有领域中被引用最多的论文。论文下载,请猛戳这里。
文中,作者通过实验总结了ResNet的几个优势:
1) Our extremely deep residual nets are easy to optimize, but the counterpart “plain” nets (that simply stack layers) exhibit higher training error when the depth increases;
1)我们的深度残差网很容易优化,但是相对的“平原”网(简单的叠加层)在深度增加时表现出更高的训练误差。
2) Our deep residual nets can easily enjoy accuracy gains from greatly increased depth, producing results substantially better than previous networks
2)我们的深度残差网可以很容易地从深度的大幅增加中获得精度(accuracy)增益,产生比以前的网络更好的结果。
二、神经网络越深越好?
从经验来看,网络的深度对模型的性能至关重要,当增加网络层数后,网络可以进行更加复杂的特征模式的提取,所以当模型更深时理论上可以取得更好的结果。但是,网络深度越深其效果就越好吗?
其实不然,经大量实践表明,神经网络随着层数的增加可能会出现两个问题:accuracy degradation problem(精度下降问题)和gradient vanishing/exploding problem(梯度消失/爆炸问题)。
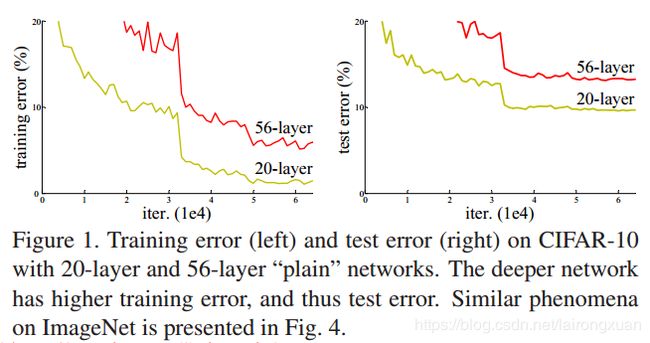
1)Accuracy degradation problem(精度下降问题)
Unexpectedly, such degradation is not caused by overfitting, and adding more layers to a suitably deep model leads to higher training error, as reported in [10, 41] and thoroughly verified by our experiments.
出乎意料的是,这种退化并不是由过拟合引起的,在一个合适的深度模型中增加更多的层会导致更高的训练误差,正如文献[10,41]所说的,我们的实验也完全验证了这一点。
2)Gradient vanishing/exploding problem(梯度消失/爆炸问题)
This problem, however, has been largely addressed by normalized initialization [23, 8, 36, 12] and intermediate normalization layers [16], which enable networks with tens of layers to start converging for stochastic gradient descent (SGD) with backpropagation [22]
然而,这个问题主要通过归一化初始化[23、8、36、12]和中间规归一化层来解决[16],通过反向传播使得具有数十层的神经网络能够收敛到随机梯度下降(SGD) [22]
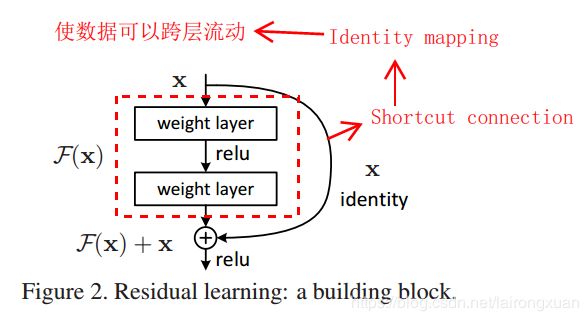
为了解决这些问题,作者提出了Deep Residual Networks,引入了残差的概念。如Figure 2所示(结构称之为一个residual block),右侧带箭头的曲线表示恒等映射,其实现了数据的跨层流动。我们想象一下,在引入恒等映射前(即没有右侧曲线),网络的输入为 x x x,经红色方框所表示的简单堆叠的网络层后得到一个输出,它是关于权重 w ′ w^\prime w′和输入 x x x的函数,我们写成 F ′ ( x , w ′ ) F^\prime(x,w^\prime) F′(x,w′)。而训练网络的最终目的就是找到一组权重 w ′ w^\prime w′,使 F ′ ( x , w ′ ) F^\prime(x,w^\prime) F′(x,w′)最逼近真实的函数 H ( x ) H(x) H(x),用式子可表示为 F ′ ( x , w ′ ) → H ( x ) F^\prime(x,w^\prime) \to H(x) F′(x,w′)→H(x)
但是现实生活中,真实的函数 H ( x ) H(x) H(x)往往非常复杂,想要找到一个足够逼近的函数 F ′ ( x , w ′ ) F^\prime(x,w^\prime) F′(x,w′)比较困难,所花费的代价也较大,作者另辟蹊径大大较小了工作量。
作者的思路是引入恒等映射。如Figure2所示,网络的输入依然还是 x x x,网络在输出之前还叠加了一次输入 x x x,网络结构发生了变化, w ′ w^\prime w′变成了是 w w w, F ′ ( x , w ′ ) F^\prime(x,w^\prime) F′(x,w′)变成了 F ( x , w ) F(x,w) F(x,w)。训练网络的目的也发生了改变,变成了找到一组权重 w w w使得 F ( x , w ) + x → H ( x ) F(x,w) +x \to H(x) F(x,w)+x→H(x),即 F ( x , w ) → H ( x ) − x F(x,w) \to H(x) - x F(x,w)→H(x)−x。如果 F ( x , w ) F(x,w) F(x,w)的所有权重都为0,则网络就是恒等映射。
那么,这种结构到底是什么意思呢?如何理解这种结构?请看后面。。。。。
二、论文中几个关键名词解释
Identity Mapping(恒等映射)
来自百度百科:
对任意集合A,如果将映射 f : A → A f:A \to A f:A→A定义为 f ( x ) = x f(x)=x f(x)=x,即规定A中每个元素 x x x与自身对应,则称 f f f为 A A A上的恒等映射。
在ResNet中,将输入直接跨层引到更深的网络层上作为输入的一部分,这个过程称之为恒等映射。恒等映射使得数据可以在网络中实现跨层流动。论文中提到:
Identity shortcut connections add neither extra parameter nor computational complexity
Identity shortcut connections既不会增加额外的更多的参数,也不会增加网络计算的复杂度。
Shortcut Connections(快捷连接)
在ResNet网络结构图中,shortcut connections就是identity mapping在网络结构图中的具体实现,也就是右侧弯曲的那条线。它既不会增加额外的更多的参数,也不会增加网络计算的复杂度。
Plain Networks(平原网络)
平原网络是作者对残差网络改进之前的简单堆叠多个layers的称呼,是和残差网络(Residual Networks)相对的一个概念。
Residual Mapping(残差映射)
对于平原网络(Plain Networks),输入 x x x后得到输出 F ( x ) F(x) F(x),这个过程可以看成一个映射过程,这个映射就称之为残差映射(Residual Mapping)。
三、几个关键问题
下面记录在看论文时,个人认为的文章重点问题:
Question 1:如何理解ResNet的Idea?
理论上来说,深层网络所映射的函数比浅层网络映射的函数要复杂得多,对现实项目中函数的逼近能力更强,但作者通过实验证明,深层网络并没有比浅层网络有等同或更高的精度,造成这种现象的原因前面也说明了。
如果现在我们要训练一个深层的网络,假设存在一个性能最强的完美网络 N N N,与它相比,我们所训练的网络中必定有一些层是多余的(甚至是起反作用的),那么这些多余的层的训练目标就是恒等变换(换句话说,就是让这些多余的层变成一个恒等变换,使得整个网络无限趋近于完美网络 N N N),只有达到这个目标我们的网络性能才能跟 N N N一样。
那么,如何另这些多余的层变成恒等映射呢?很简单,要想多余的层变成恒等映射,只要把输出所要拟合的目标变成 x x x就行了(此时 H ( x ) H(x) H(x)摇身一变成了 x x x),即输入为 x x x,输出仍然是 x x x。
因此,作者提出了利用残差来重构网络的映射,说白了就是把输入 x x x再次引入到结果,这样堆叠层的权重会趋向于零,用表达式表示就是: F ( x , w ) + x = H ( x ) = x F(x,w) + x = H(x) = x F(x,w)+x=H(x)=x,即 F ( x , w ) → 0 F(x,w) \to 0 F(x,w)→0。
总结一句话:残差结构人为制造了恒等映射,就能让整个结构朝着恒等映射的方向去收敛,确保最终的错误率不会因为深度的变大而越来越差。
Question 2:引入残差为何可以更好的训练?
残差的思想都是去掉相同的主体部分,从而突出微小的变化,引入残差后的映射对输出的变化更敏感。如何理解?我们来看一个例子:
假设:在引入残差之前,输入 x = 6 x=6 x=6,要拟合的函数 H ( x ) = 6.1 H(x)=6.1 H(x)=6.1,也就是说平原网络找到了一组 w ′ w^\prime w′使得 F ′ ( x , w ′ ) → H ( x ) = 6.1 F^\prime (x,w^\prime) \to H(x)=6.1 F′(x,w′)→H(x)=6.1。引入残差后,输入不变还是 x = 6 x=6 x=6,要拟合的函数 H ( x ) = 6.1 H(x)=6.1 H(x)=6.1,变化的是 F ( x , w ) + x → H ( x ) ) = 6.1 F(x,w)+x \to H(x))=6.1 F(x,w)+x→H(x))=6.1,可得 F ( x , w ) → 0.1 F(x,w) \to 0.1 F(x,w)→0.1。
如果需拟合的函数 H ( x ) H(x) H(x)增大了0.1,那么对平原网络来说 F ′ ( x , w ′ ) F^\prime (x,w^\prime) F′(x,w′)就是从6.1变成了6.2,增大了1.6%。而对于ResNet来说, F ( x , w ) F(x,w) F(x,w)从0.1变成了0.2,增大了100%。很明显,在残差网络中输出的变化对权重的调整影响更大,也就是说反向传播的梯度值更大,训练就更加容易。
Question 3:ResNet如何解决梯度消失问题?
我们想象这么一个ResNet,它由 L L L个residual block组成,即多个如Figure 2所示的单元构成。每一个单元的输入和输出表示为 x l x_l xl和 x l + 1 x_{l+1} xl+1。那么我们可得如下公式:
y L = h ( x L ) + F ( x L , w L ) = w s x L + F ( x L , w L ) x L + 1 = f ( y L ) y_L = h(x_{L}) + F(x_{L},w_{L}) = w_s x_{L} + F(x_{L},w_{L}) \\ x_{L+1} = f (y_L) yL=h(xL)+F(xL,wL)=wsxL+F(xL,wL)xL+1=f(yL)
有两个假设:1) x L + 1 = f ( y L ) = y L x_{L+1} = f (y_L) = y_L xL+1=f(yL)=yL;2) w s = I w_s = I ws=I,即 w s w_s ws为单位矩阵,即 h ( x L ) = x L h(x_{L}) = x_{L} h(xL)=xL。所以有:
x L = x L − 1 + F ( x L − 1 , w L − 1 ) = x 0 + ∑ i = 0 L − 1 F ( x i , w i ) = x l + ∑ i = l L − 1 F ( x i , w i ) x_L = x_{L-1} + F \left( x_{L-1}, w_{L-1} \right) \\ = x_0 + \sum_{i=0}^{L-1} F(x_i,w_i) \\ = x_l + \sum_{i=l}^{L-1} F(x_i,w_i) xL=xL−1+F(xL−1,wL−1)=x0+i=0∑L−1F(xi,wi)=xl+i=l∑L−1F(xi,wi)
在反向传播过程中,另 E E E为总误差,则有下列求导过程:
∂ E ∂ x l = ∂ E ∂ x L ⋅ ∂ x L ∂ x l = ∂ E ∂ x L ⋅ ∂ ∂ x l ( x l + ∑ i = l L − 1 F ( x i , w i ) ) = ∂ E ∂ x L ⋅ ( 1 + ∑ i = l L − 1 ∂ ∂ x l F ( x i , w i ) ) \frac{ \partial E }{ \partial x_l } = \frac{\partial E}{\partial x_L} \cdot \frac{\partial x_L}{\partial x_l} = \frac{\partial E}{\partial x_L} \cdot \frac{\partial}{\partial x_l} \left( x_l + \sum_{i=l}^{L-1} F(x_i,w_i) \right) = \frac{\partial E}{\partial x_L} \cdot \left( 1 + \sum_{i=l}^{L-1} \frac{\partial}{\partial x_l} F(x_i,w_i) \right) ∂xl∂E=∂xL∂E⋅∂xl∂xL=∂xL∂E⋅∂xl∂(xl+i=l∑L−1F(xi,wi))=∂xL∂E⋅(1+i=l∑L−1∂xl∂F(xi,wi))
式子的第一个因子 ∂ E ∂ x L \frac{\partial E}{\partial {{x}_{L}}} ∂xL∂E表示的损失函数到达 L 的梯度,小括号中的1表明短路机制可以无损地传播梯度,而另外一项残差梯度则需要经过带有权重的层,梯度不是直接传递过来的。很显然,造成梯度消失的根本原因——梯度连乘不复存在了。残差梯度不会那么巧全为-1,而且就算其比较小,有1的存在也不会导致梯度消失。
需要注意,上述两个假设是必不可少的,否则如上关系不再成立。论文中提到,经实践证明,令 w s w_s ws为单位矩阵是最优的选择。
Reference
[1] Deep Residual Network 深度残差网络
[2] Deep Residual Networks(ResNet) 简介
[3] 获奖无数的深度残差学习,清华学霸的又一次No.1
[4] Deep Residual Network学习(一)
[5] 残差网络(Deep Residual Learning for Image Recognition)
[6] resnet(残差网络)的F(x)究竟长什么样子?
[7] 深度学习网络篇——ResNet
[8] Residual Networks 理解
[9] 残差网络ResNet解读(原创)
[10] 你必须要知道CNN模型:ResNet