《FCOS: Fully Convolutional One-Stage Object Detection》论文详解

《FCOS: Fully Convolutional One-Stage Object Detection》发表于ICCV2019

代码地址：https://github.com/tianzhi0549/FCOS/

这篇文章主要是觉得现有的基于anchor的目标检测器存在一些缺点：

1. 检测结果对于anchor的大小，尺度比例，数量比较敏感
2. 即使认真的调好的上述参数，检测器对于GT变化较大，特别是小物体效果较差
3. 为了获得较高的召回率，基于anchor的检测器需要大量的anchor
4. anchor会涉及一些复杂的计算，比如计算anchor与GT的IoU

一、网络结构

该文章的网络结构如下图所示

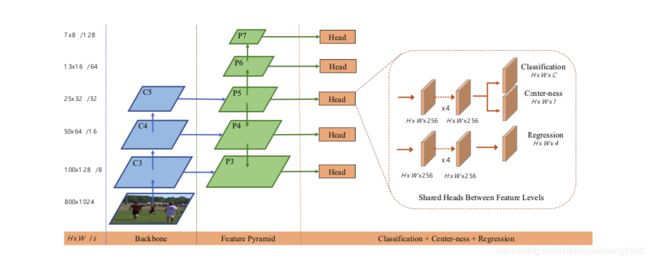
可以看出，网络结构还是backbone+fpn的结构。文中backbone采用的是resnet50。FPN结构中，$\{P_3,P_4,P_5,P_6,P_7\}$中$P_3,P_4,P_5$分别是$C_3,C_4,C_5$分别接一个$1\times 1$的卷积接上上一层的结果（这里的连接要看具体实现，可能是concate也可能是加），$P_6,P_7$分别是$P_5,P_6$通过一个stride为2的卷积得到。这样得到的$\{P_3,P_4,P_5,P_6,P_7\}$对应原图缩小的尺度分别是8，16，32，64，128。

网络的输入下面详解介绍GT的产生。网络的输出的head部分有三个分支，其中classification和regression分支与其它检测器是一样的，另外网络还加了一个叫Center-ness的分支，要了解这个分支要先知道网络的GT是什么，下面先介绍网络的标签生成。

二、网络的标签生成

2.1 样本的标签生成

不同于基于anchor的方法（通过回归anchor的坐标点来获得预测框），本文的做法是通过直接回归对应点到GT的四条边的距离来获得预测框。

上述FPN输出的feature map这里用$F_i$表示，在$F_i$上坐标为（x,y）的点，对应到原图的坐标为$(\lfloor \frac{s}{2}\rfloor +xs,\lfloor \frac{s}{2}\rfloor +ys)$，如果该点在标注框内，我们将它定义为正样本，否则为负样本。

对于一个标注框{B_i}来说，这里$B_i=(x_0^i,y_0^i,x_1^i,y_1^i,c^i)$，其中$(x_0^i,y_0^i)$表示标注框的左上角，$(x_1^i,y_1^i)$表示标注框的右下角，$c^i$表示标注框的所属类别。对于一个图像中（注意这里是图像中，不是上述的featuremap中），一个在标注框内坐标为(x,y)的正样本，GT用下述公式表示：
$l^{\ast }=x-x_0^i,t^{\ast }=y-y_0^i$
$r^{\ast }=x_1^i-x,b^{\ast }=y_1^i-y$
类别标签对于正样本来说就是$c^i$，对于负样本来说为0。
回归目标$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })$如下图所示

2.2 正负样本在不同FPN层的分配

因为采用了FPN的结构，在基于anchor的算法中，通过anchor的大小，将anchor分配给不同的FPN输出层。对于本文算法来说将正样本分配给不同FPN层的规则如下：
如果$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })>m_i$或$(l^{\ast },t^{\ast },r^{\ast },b^{\ast })<m_{(i-1)}$，那么$F_i$上满足条件的为负样本。换句话说就是在$F_i$上满足$m_{(i-1)}<(l^{\ast },t^{\ast },r^{\ast },b^{\ast })<m_i$条件的点位正样本。文章规定$m_2,m_3,m_4,m_5,m_6,m_7$大小为0， 64， 128， 256， 512， $\infty$。

2.3 模棱两可的正样本分配问题

在实际情况中，框可能存在重叠问题，那么就会有重叠区域的像素可以对应于两个或者多个标注框，文章将这种模棱两可的正样本分配给面积小的框，即这类的点用来回归小框。

三、网络的loss函数

与其他的目标检测类似，网络的loss函数可以用下式表示：
$L(\{p_{x,y}\},\{t_{x,y}\})=\frac{1}{N}{\sum }_{x,y}{L}_{cls}(P_{x,y},c_{x,y}^{\ast })+\frac{\lambda }{N_{pos}}{\sum }_{x,y}{1}_{\{c_{x,y}^{\ast }>0\}{L}_{reg}(t_{x,y},t_{x,y}^{\ast })}$

其中$L_{cls}$使用的是focal loss，$L_{reg}$使用的是IOU loss，$N_{pos}$表示的是正样本的个数，这里$\lambda$取1，$1_{c_i^{\ast }>0}$表示当$c_i^{\ast }>0$时值取1否则取0。

这里只使用了两个分支，通过上述结构和loss实验发现FCOS的结果与基于anchor的方法的结果还是存在一些差距。观察发现，造成这种现象的原因是一些远离标注框中心的点预测出来的框质量较低，为了改善这一现象，文中提出了centerness的概念。

centerness就是在原网络分类分支上加了一个sibling分支，这个分支的作用是来描述正样本点对于待预测的标注框中心点的归一化距离的大小。对于这个分支待预测的目标，也就是该分支的GT为
$centerness\ast =\sqrt{\frac{min(l^{\ast },r^{\ast })}{max(l^{\ast },r^{\ast })}\times \frac{min(t^{\ast },b^{\ast })}{max(t^{\ast },b^{\ast })}}$
这个目标值的范围为0-1，所以这个分支的loss采用交叉熵loss计算。

对于测试阶段，预测框的分数为分类分支的结果乘以centerness分支预测的结果，这样对于离标注框中心较远的点预测的分数有一定的权重衰减，从而提高最终网络的输出质量。centerness的预测目标如下图所示，图中红色表示1蓝色表示0，其它颜色在0-1之间。

到这里FCOS算法就介绍完了，详细的实验结果可以查看原文了解。