高等数学（下）知识点总结（1）

高等数学（下）知识点总结

期末，总结一下高数下的知识点

第八章_空间解析几何和向量代数

这一章是后面重积分学习的基础，比较简单。

8.1 向量运算

1、向量的概念：既有大小又有方向，且满足平行四边形法则的量称为向量。

2、向量的运算：
数量积：$a\cdot b$ = $|a|\cdot |b|\cdot cos\theta$
$a在b上的投影为|a|cos\theta =PrJab$
向量积：$a\times b=|a|\cdot |b|\cdot sin\theta$ （运用行列式对空间向量计算简单易记）
混合积：$(a\times b)\cdot c$记作$[abc]$

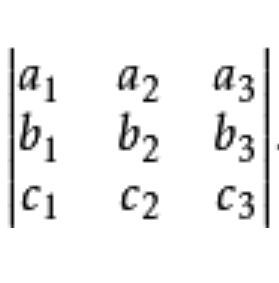
（混合积的行列式表示）

8.2 平面及其方程

1、点法式方程
已知平面的法向量$n=(A,B,C)$且过点$M_0(x_0,y_0,z_0)$，则$A(x-x_0)+B(y-y_0)+C(z-z_0)=0$

2、三点式方程

3、截距式方程
已知三个坐标轴的截距$a,b,c$，则$x/a+y/b+z/c=0$

4、一般式放程
$Ax+By+Cz+D=0$

5、面与面的夹角即求两平面法向量$n_1=(A_1,B_1,C_1),n_2=(A_2,B_2,C_2),则cos\theta =|n_1\cdot n_2|/|n_1|\cdot |n_2|$

6、距离公式
点到平面间距离公式：$d=A{x}_0+B{y}_0+C{z}_0+D/\sqrt{A^2+B^2+C^2}$
两平行平面间的距离：$d=|D_1-D_0|/\sqrt{A^2+B^2+C^2}$

8.3 空间中的线面方程

1、直线方程
1）对称式方程：已知直线过点$M_0(x_0,y_0,z_0)$，方向向量$s=(m,n,q)$，则直线方程为$\frac{x-x_0}{m}=\frac{y-y_0}{n}=\frac{z-z_0}{q}$(当某些分母为0时，分子理解为等于0)
2）参数式方程：$x=x_0+mt,y=y_0+nt,z=z_0+qt$（t为参数）
3）一般式方程：$A_{1}x+B_{1}y+C_{1}z+D_1=0,A_{2}x+B_{2}y+C_{2}z+D_2=0$
4）两直线夹角为其方向向量夹角

5）线面夹角为面的法向量与线的方向向量夹角的余角
6）平面束方程为$A_{1}x+B_{1}y+C_{1}z+D_1+\lambda (A_{2}x+B_{2}y+C_{2}z+D_2)=0$

2、曲面方程
1）旋转曲面：一条平面曲线绕其平面上一条定直线旋转一周所形成的曲面叫做旋转曲面（旋转曲面的方程由平面曲线变化而来，遵循绕固定轴旋转则该变量不变的特点）
2）柱面：平行定直线并沿定曲线 $C$ 移动的直线 $l$形成的轨迹叫做柱面，&C&叫做准线，$l$ 叫做母线
3）二次曲面：
a>椭球面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}+\frac{z^2}{c^2}=1$
b>抛物面：椭圆抛物面：$\frac{x^2}{2p}+\frac{y^2}{2q}=z$（p,q同号），双曲抛物面：$\frac{x^2}{2p}-\frac{y^2}{2q}=z$（p,q同号）
c>双曲面：单叶双曲面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{y^2}{c^2}=1$（a,b,c为正数）,双叶双曲面：$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{y^2}{c^2}=-1$（a,b,c为正数）
d>椭圆锥面：$\frac{x^2}{a^2}+\frac{x^2}{b^2}=z^2$

3、空间曲线及其方程：两曲面的交线。具体意义不大，做了解，举例螺旋线$x=acos\theta ,y=asin\theta ,z=b\theta$

第九章_多元函数微分法及其应用

几个琐碎的知识点

1、区域
2、内点，外点，边界点
3、聚点
4、开区域和闭区域
5、n维空间$R^n$
6、多元函数的概念：（参考一元函数的相关定义去理解）
这里提一下用定义判断极限存在否，并计算（除洛必达不可用，其他对于一元函数极限求法很多都可参考）
连续性的判定：①函数在$p_0$有定义②极限存在③极限值等于函数值
且多元函数满足：①有界性定理②最值定理③介值定理

9.1偏导数

总体思路为固定其他变量，只改变一个变量，此时转化为一元函数求导的情况。

（几何意义如下图所示）

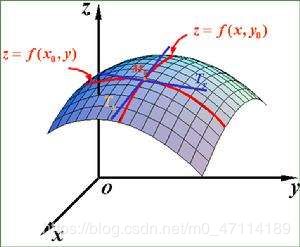
注意：偏导数存在不一定连续（一元函数可导必连续）
对于初等函数，高阶偏导数与求导顺序无关

9.2 全微分

1、函数的偏增量：对x的偏增量 $f(x+\Delta x,y)-f(x,y)$，对y的偏增量 $f(x,y+\Delta y)-f(x,y)$

2、函数的全增量：$\Delta z=f(x+\Delta x,y+\Delta y)-f(x,y)$
如果函数的全增量可以表示为$\Delta z=A\Delta x+B\Delta y+o(\rho ),\rho =\sqrt{\Delta x^2+\Delta y^2}$ 那么函数在$(x,y)$处可微

3、全微分存在条件：
1）若函数在$(x,y)$该点可微，则函数在该点连续
2）若函数在$(x,y)$该点可微，则函数在该点偏导数$\frac{\partial z}{\partial x},\frac{\partial z}{\partial y}$存在且$dz=\frac{\partial z}{\partial x}\Delta x+\frac{\partial z}{\partial y}\Delta y$
注意：上面两个条件都是必要条件，不是充要条件
3）若函数偏导数存在且连续，则函数在该点可微
注意：这个条件是充分条件，而不是充要条件

9.3复杂的函数求导

1、多元复合函数求导
同样遵从链式法则，不多说

2、隐函数求导
1）对于一个方程而言，如果①点$P(x_0,y_0,z_0)$的某邻域内具有连续偏导数②$F(x_0,y_0,z_0)=0$③$F_z(x_0,y_0,z_0)!=0$可直接采取两边同时求（偏）导的方法，也可采用公式$\frac{\partial z}{\partial x}=-\frac{F_x}{F_z},\frac{\partial z}{\partial y}=-\frac{F_y}{F_z}$
2）对于方程组而言，公式法不便记忆，不提倡。建议采用直接法，解线性方程组。

9.4多元函数微分法的应用

1、一元向量值函数（$R^3$）
$f(t)=(\phi (t),\varphi (t),z(t))$
极限：${\lim }_{t\to t_0}f(t)=f(t)=({\lim }_{t\to t_0}\phi (t),{\lim }_{t\to t_0}\varphi (t),{\lim }_{t\to t_0}z(t))$
连续：${\lim }_{t\to t_0}f(t)=f(t_0)$
导数：$f^{\prime }(t)=({\phi }^{\prime }(t),{\varphi }^{\prime }(t),z^{\prime }(t))$
几何意义：切向量$f^{\prime }(t_0)=({\phi }^{\prime }(t_0),{\varphi }^{\prime }(t_0),z^{\prime }(t_0))$的指向与t的增长方向一致

2、空间曲线的切线和法平面
给定光滑曲线$f(t)=(\phi (t),\varphi (t),z(t))$，切向量为$f^{\prime }(t)=({\phi }^{\prime }(t),{\varphi }^{\prime }(t),z^{\prime }(t))$，切线方程：$\frac{x-x_0}{{\phi }^{\prime }(t_0)}=\frac{y-y_0}{{\varphi }^{\prime }(t_0)}=\frac{z-z_0}{z^{\prime }(t_0)}$法平面方程为：${\phi }^{\prime }(t_0)(x-x_0)+{\varphi }^{\prime }(t_0)(y-y_0)+z^{\prime }(t_0)(z-z_0)=0$

3、曲面的切平面和法线
设有光滑曲面$\Sigma :F(x,y,z)=0$，通过其定点$M(x_0,y_0,z_0)$任意引一条光滑曲线$x=\phi (t),y=\varphi (t),z=z(t)$，设$t_0=t$对应$M$点，且${\phi }^{\prime }(t),{\varphi }^{\prime }(t),z^{\prime }(t)$不全为0，则在$M$点的切向量：$T=({\phi }^{\prime }(t),{\varphi }^{\prime }(t),z^{\prime }(t))$，切向方程为：$\frac{x-x_0}{{\phi }^{\prime }(t_0)}=\frac{y-y_0}{{\varphi }^{\prime }(t_0)}=\frac{z-z_0}{z^{\prime }(t_0)}$
曲面$\Sigma :F(x,y,z)=0$在点$M(x_0,y_0,z_0)$的法向量：$n=(F_x(M),F_y(M),F_z(M))$，切平面方程：$F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0$，法线方程：$\frac{x-x_0}{F_x}=\frac{y-y_0}{F_y}=\frac{z-z_0}{F_z}$

4、全微分的几何意义
曲面方程$z=f(x,y)$在$M$处切平面的方程为
$z-z_0=f_x(x-x_0)+f_y(y-y_0)$
（切平面上点竖坐标的增量）$z-z_0=（$z = f(x,y)$在点$(x_0,y_0)$的全微分）f_x(x-x_0)+f_y(y-y_0)$函数

5、法向量的方向余弦
法向量$n=(-f_x(x-x_0)，-f_y(y-y_0)，1)$
与x轴正方向夹角$cos\alpha =\frac{-f_x}{\sqrt{1+f_x^2+f_y^2}}$
与y轴正方向夹角$cos\beta =\frac{-f_y}{\sqrt{1+f_x^2+f_y^2}}$
与z轴正方向夹角$cos\gamma =\frac{-f_z}{\sqrt{1+f_x^2+f_y^2}}$

9.5方向导数和梯度

1、方向导数
设$z=f(x,y)$在$p_0$处可微，则$f(x,y)$在$P_0$沿任意方向$l$的方向导数存在，$l$的单位向量为$e_1=(cos\alpha ,cos\beta )$，则$\frac{\partial f}{\partial l}=f_{x}cos\alpha +f_{y}cos\beta$（推广到三维同理）

2、梯度
$\frac{\partial f}{\partial l}=f_{x}cos\alpha +f_{y}cos\beta =(f_x,f_y)(cos\alpha ,cos\beta )$其中$G=(f_x,f_y)$称为梯度向量，简称梯度
梯度是函数增长最快的方向

9.6 多元函数的极值及其求法

1、极值
1）函数$z=f(x,y)$在点$(x_0,y_0)$存在偏导数，且在该点取得极值，则$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$
2）函数$z=f(x,y)$在点$(x_0,y_0)$的某邻域内里拦蓄且有一阶和二阶连续偏导数，又$f_x(x_0,y_0)=0,f_y(x_0,y_0)=0$，令$A=F_{xx}(x_0,y_0),B=F_{xy}(x_0,y_0),C=F_{yy}(x_0,y_0),$
则若$AC-B^2>0$具有极值（$A<0有极大值，A>0有极小值$）
若$AC-B^2<0$没有极值
若$AC-B^2=0$无法确定

2、最值
可能的最值点：内部（驻点，不可导点）&边界
条件极值：拉格朗日数乘法

第十章_重积分

第十一章_几类特殊的积分

第十二章_无穷级数

后记

内容太多了，写了一下午了，实在一次写不完了，分成两部分吧，下次接着写第十章，第十一章，第十二章，先把这一部分发出来。