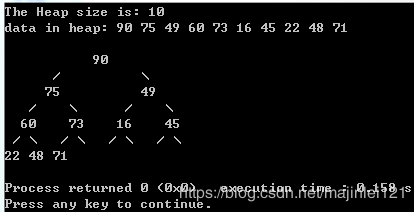
数据结构与算法C++之堆排序

首先需要介绍一下一个新的数据结构：堆
堆使用了优先队列
普通队列：先进先出，后进后出
优先队列：出队顺序与入队顺序无关，与优先级有关，一般取出优先级最高的元素，堆入队出队的算法复杂度都为O(nlogn)
最常使用的是二叉堆（Binary Heap）

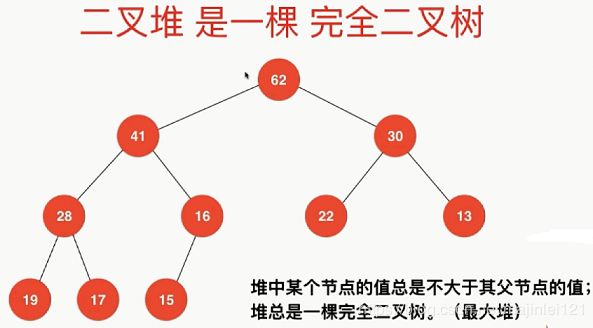
如上图所示，62称为41和30的父节点，41称为左节点，30称为右节点，以此类推，41又是28和16的父节点，等等，二叉堆有如下性质：

• 父节点大于左右子节点
• 堆总是一棵完全二叉树，即最后一层上面的所有层都是完整的，即因为上图有四层，那么30一定同时存在左右节点，否则就不满足堆的性质，倒数第二层的父节点可以左右节点都没有，如22，也可以只有一个节点，但这个节点必须是左节点，如16
  用数组来存储二叉堆，如下图所示
  

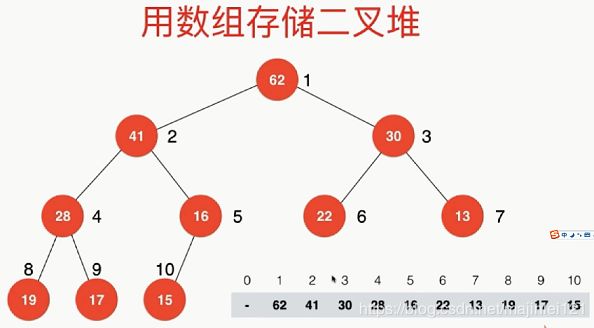
习惯于将最上面的父节点62编号为1，然后从上到下，从左到右依次编号，因为编号从1开始，所以用来存储堆的数组需要10+1个存储空间

• 定义某个节点 $i$ 的父节点为 $parent(i)=i/2$
• 定义该节点 $i$ 的左节点为 $leftchild(i)=2\ast i$
• 定义该节点$i$ 的又节点为 $rightchild(i)=2\ast i+1$

如节点4，它的值是28，他的父节点为 $4/2=2$，值是41
它的左节点为 $2\ast 4=8$，值是19
它的右节点为 $2\ast 4+1=9$, 值是17

Shift Up 堆中插入元素

如上图所示，插入元素值为52

（1）首先将52插入堆的最后一个位置，编号为11

（2）将52与其父节点16作比较，比16大，那么交换16和52的位置

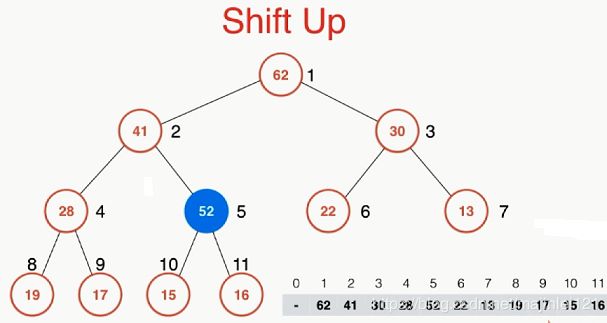
（3）将52再与其父节点41作比较，比41大，那么交换41和52的位置

（4）将52再与新的父节点62作比较，比62小，那么插入操作结束

Shift Down 堆中取出最大元素

（1）首先将最上面的父节点62取出

（2）将最后一个节点16填补到最上面的位置，同时将堆的元素总数count减1

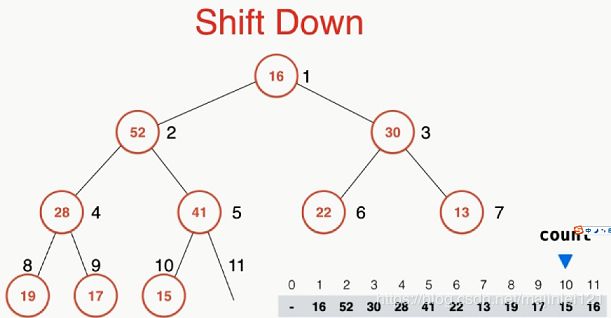
（3）然后将父节点16与其他两个子节点52和30作比较，16比52小，那么交换16与52的位置

（4）继续比较16与它的两个新的子节点28和41的大小，比41小，那么交换16和41的位置

（4）继续比较16与其子节点15的大小，16比15大，那么不用交换位置，Shift Down结束

下面就先使用ShiftUp和ShiftDown进行插入元素和取出元素

#include 
#include 
#include 
#include 
#include 
#include 
#include 

#ifndef _SORTINGHELP_H_
#define _SORTINGHELP_H_
#include "SortingHelp.h"
#endif // _SORTINGHELP_H_

#include "MergeSorting.h"
#include "quickSorting.h"

using namespace std;

template<typename Item>
class MaxHeap{
private:
    Item *data;
    int count;
    int capacity;

    void ShiftUp(int k){
        while (data[k/2] < data[k] && k > 1){
            swap(data[k/2], data[k]);
            k /= 2;
        }
    }

    void ShiftDown(int k){
        while (k <= count/2){
            int j = 2*k; //此轮循环中，data[k]和data[j]交换位置
            if (data[j] < data[j+1] && j + 1 <= count)
                j += 1;
            if (data[k] >= data[j])
                break;

            swap(data[j], data[k]);
            k = j;
        }
    }

public:
    MaxHeap(int capacity){
        data = new Item[capacity + 1];
        count = 0;
        this->capacity = capacity;
    }

    ~MaxHeap(){
        delete[] data;
    }

    int size(){
        return count;
    }

    bool isEmpty(){
        return count == 0;
    }

    void insert(Item item){

        assert( count + 1 <= capacity );
        data[count+1] = item;
        count ++;
        ShiftUp(count);
    }

    Item extractMax(){
        assert( count > 0);

        Item ret = data[1];

        swap(data[1], data[count]);
        count --;
        ShiftDown(1);

        return ret;
    }

public:
    void testPrint(){ //打印堆函数，不用掌握

        if( size() >= 100 ){
            cout<<"Fancy print can only work for less than 100 int";
            return;
        }

        if( typeid(Item) != typeid(int) ){
            cout <<"Fancy print can only work for int item";
            return;
        }

        cout<<"The Heap size is: "<<size()<<endl;
        cout<<"data in heap: ";
        for( int i = 1 ; i <= size() ; i ++ )
            cout<<data[i]<<" ";
        cout<<endl;
        cout<<endl;

        int n = size();
        int max_level = 0;
        int number_per_level = 1;
        while( n > 0 ) {
            max_level += 1;
            n -= number_per_level;
            number_per_level *= 2;
        }

        int max_level_number = int(pow(2, max_level-1));
        int cur_tree_max_level_number = max_level_number;
        int index = 1;
        for( int level = 0 ; level < max_level ; level ++ ){
            string line1 = string(max_level_number*3-1, ' ');

            int cur_level_number = min(count-int(pow(2,level))+1,int(pow(2,level)));
            bool isLeft = true;
            for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index ++ , index_cur_level ++ ){
                putNumberInLine( data[index] , line1 , index_cur_level , cur_tree_max_level_number*3-1 , isLeft );
                isLeft = !isLeft;
            }
            cout<<line1<<endl;

            if( level == max_level - 1 )
                break;

            string line2 = string(max_level_number*3-1, ' ');
            for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index_cur_level ++ )
                putBranchInLine( line2 , index_cur_level , cur_tree_max_level_number*3-1 );
            cout<<line2<<endl;

            cur_tree_max_level_number /= 2;
        }
    }

private:
    void putNumberInLine( int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft){

        int sub_tree_width = (cur_tree_width - 1) / 2;
        int offset = index_cur_level * (cur_tree_width+1) + sub_tree_width;
        assert(offset + 1 < line.size());
        if( num >= 10 ) {
            line[offset + 0] = '0' + num / 10;
            line[offset + 1] = '0' + num % 10;
        }
        else{
            if( isLeft)
                line[offset + 0] = '0' + num;
            else
                line[offset + 1] = '0' + num;
        }
    }

    void putBranchInLine( string &line, int index_cur_level, int cur_tree_width){

        int sub_tree_width = (cur_tree_width - 1) / 2;
        int sub_sub_tree_width = (sub_tree_width - 1) / 2;
        int offset_left = index_cur_level * (cur_tree_width+1) + sub_sub_tree_width;
        assert( offset_left + 1 < line.size() );
        int offset_right = index_cur_level * (cur_tree_width+1) + sub_tree_width + 1 + sub_sub_tree_width;
        assert( offset_right < line.size() );

        line[offset_left + 1] = '/';
        line[offset_right + 0] = '\\';
    }
};



int main(){
    MaxHeap<int> maxheap = MaxHeap<int>(100);
    srand(time(NULL));
    for (int i = 0; i < 10; i++){
        maxheap.insert(rand()%100);
    }
    maxheap.testPrint();
    return 0;
}

输出为

取出元素测试程序为

int main(){
    MaxHeap<int> maxheap = MaxHeap<int>(100);
    srand(time(NULL));
    for (int i = 0; i < 10; i++){
        maxheap.insert(rand()%100);
    }
    //maxheap.testPrint();
    while(!maxheap.isEmpty()){
        cout<<maxheap.extractMax()<<" ";
    }
    cout<<endl;
    return 0;
}

输出为

下面使用堆实现排序
其实就是先将数组中元素挨个放入堆中，然后挨个将堆中元素取出来逆序再放入数组中就可以
首先将堆的实现放入 Heap.h 中

//Heap.h

#include 
#include 
#include 
#include 
#include 
#include 
#include 

using namespace std;

template<typename Item>
class MaxHeap{
private:
    Item *data;
    int count;
    int capacity;

    void ShiftUp(int k){
        while (data[k/2] < data[k] && k > 1){
            swap(data[k/2], data[k]);
            k /= 2;
        }
    }

    void ShiftDown(int k){
        while (k <= count/2){
            int j = 2*k; //此轮循环中，data[k]和data[j]交换位置
            if (data[j] < data[j+1] && j + 1 <= count)
                j += 1;
            if (data[k] >= data[j])
                break;

            swap(data[j], data[k]);
            k = j;
        }
    }

public:
    MaxHeap(int capacity){
        data = new Item[capacity + 1];
        count = 0;
        this->capacity = capacity;
    }

    ~MaxHeap(){
        delete[] data;
    }

    int size(){
        return count;
    }

    bool isEmpty(){
        return count == 0;
    }

    void insert(Item item){

        assert( count + 1 <= capacity );
        data[count+1] = item;
        count ++;
        ShiftUp(count);
    }

    Item extractMax(){
        assert( count > 0);

        Item ret = data[1];

        swap(data[1], data[count]);
        count --;
        ShiftDown(1);

        return ret;
    }

public:
    void testPrint(){

        if( size() >= 100 ){
            cout<<"Fancy print can only work for less than 100 int";
            return;
        }

        if( typeid(Item) != typeid(int) ){
            cout <<"Fancy print can only work for int item";
            return;
        }

        cout<<"The Heap size is: "<<size()<<endl;
        cout<<"data in heap: ";
        for( int i = 1 ; i <= size() ; i ++ )
            cout<<data[i]<<" ";
        cout<<endl;
        cout<<endl;

        int n = size();
        int max_level = 0;
        int number_per_level = 1;
        while( n > 0 ) {
            max_level += 1;
            n -= number_per_level;
            number_per_level *= 2;
        }

        int max_level_number = int(pow(2, max_level-1));
        int cur_tree_max_level_number = max_level_number;
        int index = 1;
        for( int level = 0 ; level < max_level ; level ++ ){
            string line1 = string(max_level_number*3-1, ' ');

            int cur_level_number = min(count-int(pow(2,level))+1,int(pow(2,level)));
            bool isLeft = true;
            for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index ++ , index_cur_level ++ ){
                putNumberInLine( data[index] , line1 , index_cur_level , cur_tree_max_level_number*3-1 , isLeft );
                isLeft = !isLeft;
            }
            cout<<line1<<endl;

            if( level == max_level - 1 )
                break;

            string line2 = string(max_level_number*3-1, ' ');
            for( int index_cur_level = 0 ; index_cur_level < cur_level_number ; index_cur_level ++ )
                putBranchInLine( line2 , index_cur_level , cur_tree_max_level_number*3-1 );
            cout<<line2<<endl;

            cur_tree_max_level_number /= 2;
        }
    }

private:
    void putNumberInLine( int num, string &line, int index_cur_level, int cur_tree_width, bool isLeft){

        int sub_tree_width = (cur_tree_width - 1) / 2;
        int offset = index_cur_level * (cur_tree_width+1) + sub_tree_width;
        assert(offset + 1 < line.size());
        if( num >= 10 ) {
            line[offset + 0] = '0' + num / 10;
            line[offset + 1] = '0' + num % 10;
        }
        else{
            if( isLeft)
                line[offset + 0] = '0' + num;
            else
                line[offset + 1] = '0' + num;
        }
    }

    void putBranchInLine( string &line, int index_cur_level, int cur_tree_width){

        int sub_tree_width = (cur_tree_width - 1) / 2;
        int sub_sub_tree_width = (sub_tree_width - 1) / 2;
        int offset_left = index_cur_level * (cur_tree_width+1) + sub_sub_tree_width;
        assert( offset_left + 1 < line.size() );
        int offset_right = index_cur_level * (cur_tree_width+1) + sub_tree_width + 1 + sub_sub_tree_width;
        assert( offset_right < line.size() );

        line[offset_left + 1] = '/';
        line[offset_right + 0] = '\\';
    }
};

实现程序如下，程序中实现的快速排序与归并排序可以参考前几篇博客

#include 

#ifndef _SORTINGHELP_H_
#define _SORTINGHELP_H_
#include "SortingHelp.h"
#endif // _SORTINGHELP_H_

#include "MergeSorting.h"
#include "quickSorting.h"
#include "Heap.h"

using namespace std;


template<typename T>
void heapSorting1(T arr[], int n){
    MaxHeap<T> maxheap = MaxHeap<T>(n);
    for (int i = 0; i < n; i ++)
        maxheap.insert(arr[i]);

    for (int i = n - 1; i >=0; i--)
        arr[i] = maxheap.extractMax();
}

int main()
{
    //对普通的随机数组进行排序
    int n = 500000;
    int *arr = generateRandomArray(n, 0, n);
    int *arr2 = copyIntArray(arr, n);
    int *arr3 = copyIntArray(arr, n);
    cout<<"普通数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;

    //对近乎有序的数组进行排序
    arr = generateNearlyOrderedArray(n, 100);//生成只有200个无序元素的数组
    arr2 = copyIntArray(arr, n);
    arr3 = copyIntArray(arr, n);
    cout<<"近乎有序的数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;

    //对有大量重复元素的数组进行排序
    arr = generateRandomArray(n, 0, 10);
    arr2 = copyIntArray(arr, n);
    arr3 = copyIntArray(arr, n);
    cout<<"有大量重复元素的数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;
    return 0;
}

输出为

可以看出堆排序要慢于归并排序和快速排序，但是计算复杂度也是在允许的范围内，数据结构堆主要用于数据的动态维护
Heapify
上面程序中是将数组元素一个个插入到堆中，如下

MaxHeap<T> maxheap = MaxHeap<T>(n);
for (int i = 0; i < n; i ++)
   maxheap.insert(arr[i]);

其实还有更好的方式，即 Heapify

（1）首先将数组按顺序放入堆中，如下图所示，此时是不满足堆的性质的

（2）可以看出所有的叶子节点都是满足堆的性质的，即30,41,62,16,28

（3）第一个非叶子节点的编号为 $count/2$，也就是 $10/2=5$也就是编号为5的22

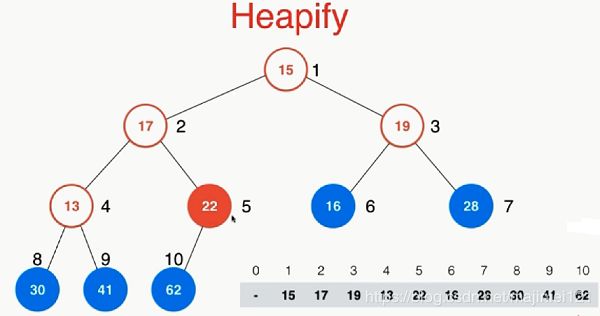
（5）找到第一个非叶子节点5后，按照5,4,3,2,1的顺序不断对他们进行ShiftDown即可，比如22比其子节点62小，那么交换22和62的位置，然后比较13和子节点30和41的大小，13比41小，交换13和41的位置，然后比较19和子节点16,28的大小，交换19和28的位置，然后比较17和子节点62,41的大小，交换17和62的位置，17继续和他的子节点比较，17比22小，那么继续交换位置，以此类推，最后就可将元素都放入正确的位置

程序实现如下，函数取名为 heapSorting2()
首先在Heap.h中添加构造函数MaxHeap(Item arr[], int n)

//Heap.h
MaxHeap(Item arr[], int n){
    data = new Item[n+1];
    capacity = n;
    for (int i = 0; i < n; i ++)
        data[i+1] = arr[i];
    count = n;
    for (int i = count / 2; i >= 1; i--)
        ShiftDown(i);
}

测试程序为

#include 

#ifndef _SORTINGHELP_H_
#define _SORTINGHELP_H_
#include "SortingHelp.h"
#endif // _SORTINGHELP_H_

#include "MergeSorting.h"
#include "quickSorting.h"
#include "Heap.h"

using namespace std;


template<typename T>
void heapSorting1(T arr[], int n){
    MaxHeap<T> maxheap = MaxHeap<T>(n);
    for (int i = 0; i < n; i ++)
        maxheap.insert(arr[i]);

    for (int i = n - 1; i >=0; i--)
        arr[i] = maxheap.extractMax();
}

//Heapify
template<typename T>
void heapSorting2(T arr[], int n){

    MaxHeap<T> maxheap = MaxHeap<T>(arr, n);

    for (int i = n - 1; i >=0; i--)
        arr[i] = maxheap.extractMax();
}

int main()
{
    //对普通的随机数组进行排序
    int n = 500000;
    int *arr = generateRandomArray(n, 0, n);
    int *arr2 = copyIntArray(arr, n);
    int *arr3 = copyIntArray(arr, n);
    int *arr4 = copyIntArray(arr, n);
    cout<<"普通数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    testSorting("heapSorting2", heapSorting2, arr4, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;

    //对近乎有序的数组进行排序
    arr = generateNearlyOrderedArray(n, 100);//生成只有200个无序元素的数组
    arr2 = copyIntArray(arr, n);
    arr3 = copyIntArray(arr, n);
    arr4 = copyIntArray(arr, n);
    cout<<"近乎有序的数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    testSorting("heapSorting2", heapSorting2, arr4, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;

    //对有大量重复元素的数组进行排序
    arr = generateRandomArray(n, 0, 10);
    arr2 = copyIntArray(arr, n);
    arr3 = copyIntArray(arr, n);
    arr4 = copyIntArray(arr, n);
    cout<<"有大量重复元素的数组进行排序"<<endl;
    testSorting("MergeSorting", MergeSorting, arr, n);
    testSorting("quickSorting2", quickSorting2, arr2, n);
    testSorting("heapSorting1", heapSorting1, arr3, n);
    testSorting("heapSorting2", heapSorting2, arr4, n);
    delete[] arr;//最后删除数组开辟的空间
    delete[] arr2;
    delete[] arr3;
    delete[] arr4;


    return 0;
}

输出为

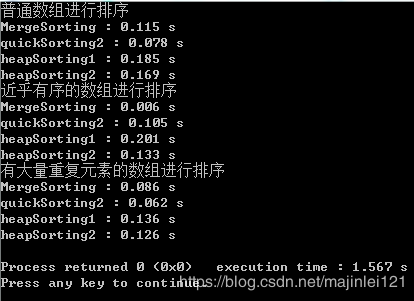
可以看出使用Heapify来将数组构造成堆后，时间变短了

• 将n个元素逐个插入到一个空堆中，算法复杂度为O(nlogn)
• heapify的过程，算法复杂度为O(n)