Matlab 数学实验----命令总结

Matlab 数学实验----命令总结

1.一元微积分实验

1.曲线绘图

曲线绘图命令主要有以下几种：

%常用
plot(x,y)  %使用前首先生成数据    x = a:b; y = f(x); plot(x,y) 
plot(x1,y1,x2,y2) 

fplot(fun,[a,b]) %使用时候需要传入函数 fun='sin(2*x)' ;fplot(fun,[a,b])

%常用
polar(theta,rho) %极坐标绘图 

%常用
ezplot(fun,[xmin,xmax]) %隐函数作图，非常方便，在接下来的例题也会大量使用

plot3(x,y,z) %用法与plot类似，首先生成数据

此外，还有一些用来调整图片格式的，比如 title 用来加标题，legend用来加图例，hold on / hold off 等等，在书上15页，此处不再赘述。

下面通过几个例题巩固对命令的理解：

例题1：立方抛物线 $y=\sqrt[3]{x}$

%使用plot绘图分为三步，首先生成数据点x，之后通过函数生成对应的数据点y，之后plot。
x = -5:0.1:0;
y=(-x)^(1/3);
y=-y;
x=0:0.1:5;
y=[y,x.^(1/3)];
x=-5:0.1:5;
plot(x,y);

例题2：做出方程 $x^4+y^4=1$ 所表示的图像

syms x y;
ezplot('x^4+y^4-1',[-1,1]);
%两句话就完事儿了，很简单有没有，不用plot生成点坐标巴拉巴拉，直接敲进去就完事儿了

例题3：笛卡尔曲线 $x^3+y^3=3xy$

%继续使用ezplot，直接敲就完事儿了
ezplot('x.^3+y.^3-3*x*y',[-5,3])

反正不管啥函数，只要不是极坐标，用ezplot，敲进去就完事儿了。

例题4：摆线 $x=t-sin(t),y=1-cos(t)$

%还记得plot的三步曲吧，这里也是一样的。
t = 0:0.1:2*pi;
x = t-sin(t);
y = t-cos(t);
plot(x,y);

例题5：星形线 $x=co{s}^{3}t,y=si{n}^{3}t,(x^{\frac{2}{3}}+y^{\frac{2}{3}}=1)$

%这就两种方法都可以了，你也可以plot像上题一样，也可以用括号里的表达式直接ezplot,这里说的够多了就不敲代码了
%。。。

例题6：阿基米德螺线 $r=\theta$

%极坐标来了，其实道理和plot差不多，还是那三步（(很啰嗦，看懂直接跳过了)）
theta = linspace(2,2*pi,100);
r = theta;
polar(theta,r);

例题7：对数螺旋线 $r=e^{\theta }$

%这里演示最后一次了，还是还是还是那三步(很啰嗦，看懂直接跳过了)
theta = linspace(2,2*pi,100);
r = exp{theta};
polar(theta,r);

---

2.极限与导数

1.极限

求极限只要记住一个命令就行了：

limit(F,x,a,'left') %简单记：函数F，在x趋于a（可以为inf）（‘left’或者'right'，分别是左右极限，可不加）时候的极限

这条命令也是一句话的事儿，这里只举一个例子：

例题1：求出下列极限

${\lim }_{x\to 1}(\frac{1}{x}-\frac{1}{e^x-1})$

limit('1/x-1/(exp(x)-1)','x',1,'left')

2.导数

syms x;
diff(F,x,n)；
%也可以不syms x，那就要在diff中加 ''了
%n表示求导阶数
%求完之后可以用simple()化简
%此处要注意求出来的是符号，因为此时x还是 syms x的状态，如果要求某个点的值，需要对x赋值之后使用eval（）

3.极值和最值

这里需要主要讲一下了，打起精神哈！

首先过一下基本的命令

[x,f] = fminbnd(F,a,b) %x是局部极小值点，f是局部极小值，F是函数，[a,b]是区间
[x,f] = fminsearch(F,x0) % 这里返回就是在x0处的极值点和极值了。

[m,k] = min(y)
[m,k] = max(y)
%上面两个命令返回最小值和最大值（老师上课讲过还有其他求解方法，可以自己思考）

接下来详解解释一道综合性比较强的例题，综合了上面讲的所有内容，顺便补充一下之前没提到的fplot知识点，之前没提是因为我个人觉得不是怎么好用，因为要解出 y=f(x)的形式，之后才能调用，但是有时候如果题中直接给你了 f(x) = … ，那fplot还是很方便的哈，具体参考下面的例子，其他看不懂的地方记得回头翻翻相关内容回忆一下：

*例题：作出下列函数以及导函数的图形，观察极值点、最值点的位置并求出，求出所有驻点以及对应的二阶导数值，求出函数的单调区间

$f(x)=x^{2}sin(x^2-x-2),[-2,2]$

ezplot('x^2*sin(x^2-x-2)-y',[-2,2]);%隐函数绘图
fplot('x^2*sin(x^2-x-2)',[-2,2])；
%题中直接给了f(x) = ...的原因，因此fplot也很方便
%顺便提一个与考试无关的，高版本的matlab已经不支持上面的写法了，最好这样写：
f=@(x)x^2*sin(x^2-x-2)
fplot('x^2*sin(x^2-x-2)',[-2,2])
%--------------------------------
%观察图像，确定极值点（极值点就是驻点，一阶导数为0的点，在这一点函数改变单调性）
%原函数在 -1 附近的极小值
[x1,f] = fminsearch('x^2*sin(x^2-x-2)',-1)
%原函数在1.5附近的极小值
[x2,f] = fminsearch('x^2*sin(x^2-x-2)',1.5)
%原函数在-1.5附近的极大值
[x3,f] = fminsearch('-x^2*sin(x^2-x-2)',-1.5)%注意加了负号
%当然还可以算原函数在上面这些极值点的函数值啦，这里演示一下，可以跳过
x=x1
f(x)%如果是符号表达式就用eval(x)，这里我因为之前用的是函数句柄
%原函数在[-2,2]最小值
x = -2:0.1:2;
y = x^2*sin(x^2-x-2);
[m,k] = min(y)
%--------------------------------
%求导数
syms x
y = x^2*sin(x^2-x-2);
dy = diff(y,x)
dy2 = diff(y,x,2) 
%作导数图像以及分析导数的极小值极大值同上面一样了
%--------------------------------
%单调区间
%上面已经求出极值点啦，单调区间就是把他们连起来。

4.方程组求根

提一下符号计算与数值计算的不同

1. 运算以推理的方式进行，不受计算误差积累问题的困扰
2. 符号计算给出完全正确的封闭解，或者任意精度的数值解
3. 计算时间长

下面介绍MATLAB命令

solve(Fun,x)%求解单个方程
[x,y] = solve(Fun1,Fun2,x,y)%求解方程组

x = fzero(Fun,[a,b])
[x,f,h]=fslove(Fun,x0)%f返回对应函数值，h返回值大于零说明结果可靠，反之不可靠

下面是例题讲解，巩固命令的掌握：

题型1：求解单个方程的解

$x^3-2x+1=0$

solve('x^3-2*x+1=0','x')%把方程原封不动敲进去就行，没啥意思

题型2：方程组的解

$x^2-y=1$

$x+y=2$

f1=('x^2-y=1')
f2=('x+y=2')
solve(f1,f2,x,y)
%两个一起敲进去，有一点意思了

fun=@(t)[t(1)^2-t(2)-1,t(1)+t(2)-2]
[t,f,h]=fsolve(fun,t)
%不知道大家看没看懂,x都换成了t(1),y都换成了t(2),使用fsolve和solve不同就在这里，solve原封不动抄进去，fsolve则要换成函数的形式，且多变量必须写成向量变量

5.不定积分与定积分

不定积分就 int()一个命令，因此就略过了，直接说定积分，问题不大。

名称	介绍
quadl	NewtonCotes积分法
trapz	梯形积分法
quad	抛物线积分法

例题：

${\int }_0^1\frac{sin(x)}{\sqrt{(1-x^2)}}dx$

syms x;
y = int(sin(x)-sqrt(1-x^2),x,0,1)
%被积表达式直接写进去，注明对x积分，之后写上下限，这是int的做法

f = @(x) sin(x)-sqrt(1-x.^2)
quad(f,0,1)
%使用函数句柄，这是quad的做法

改变积分上下啦比如上限写inf之类的还可以算广义积分，书里35页提到了瑕积分的概念，有空也可以看看。

6.级数

${\lim }_{n\to \infty }(1+\frac{1}{2}+...+\frac{1}{n}-\ln n)$

syms k n;
limit(syms(1/k,k,1,n)-log(n),inf)
%matlab中 log(n)就是 ln（n）

如果是特殊的级数，我们可以写出部分和公式，之后代入计算，如果没有symsum，我们可以用for循环代替

这一节的知识还涉及到判断级数的敛散性，绝对收敛和条件收敛，自己顺便回忆下喽~

---

2.多元微积分实验

1.曲面绘图

这一小节有两个知识点，分别是曲面绘制和等高线绘制，这里放在一起讲了，看的时候注意分别掌握。

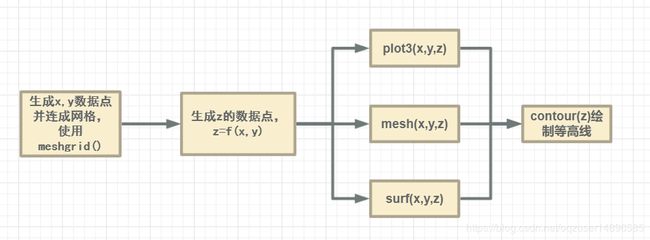
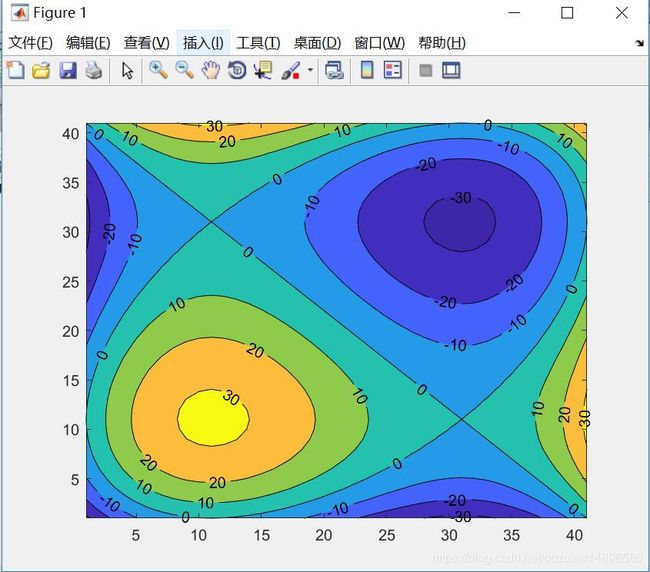
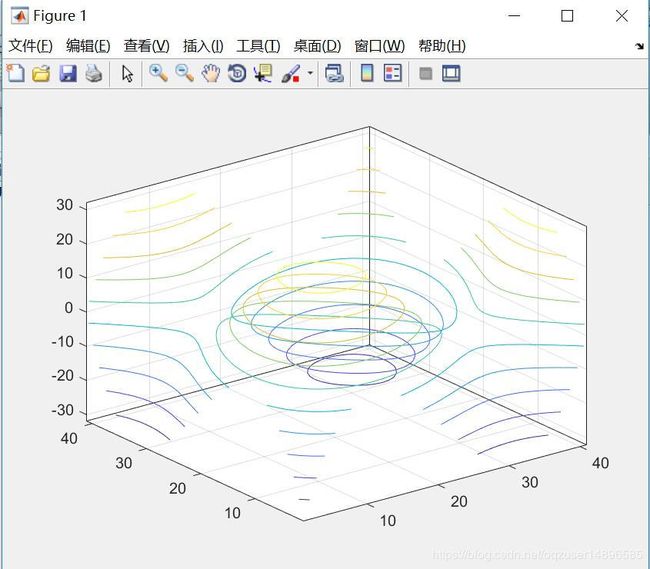
首先提一下流程，之后上代码。曲面绘制和等高线绘制其实像是一套动作，还记得plot命令如何使用吗，首先生成数据点x，之后使用函数关系生成数据点y，最后plot(x,y)，曲面绘制也是一个路子：首先生成数据点（x,y），之后用meshgrid()命令生成数据点z，最后plot3(x,y,z)。当然你也可以选择用mesh,surf等等，当当然你也可以选择用meshc,surfc等等附带等高线。之后是等高线的绘制，我们已经拿到z的数据点了，直接一句contour(z)，等高线就出来了。

下面贴了一张流程图：

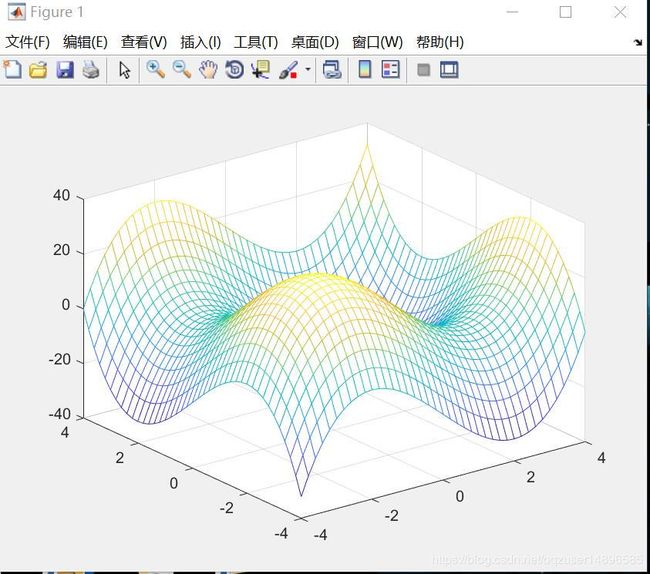
例题：画出曲面$z=x^3+y^3-12x-12y,-4⩽x,y⩽4$

[x,y] = meshgrid(-4:0.2:4) %生成数据点并连成网格
z = x.^3+y.^3-12*x-12*y;%生成数据点z
mesh(x,y,z);%绘制曲面

[x,y] = meshgrid(-4:0.2:4) %生成数据点并连成网格
z = x.^3+y.^3-12*x-12*y;%生成数据点z
meshc(x,y,z);%绘制曲面

[x,y] = meshgrid(-4:0.2:4) %生成数据点并连成网格
z = x.^3+y.^3-12*x-12*y;%生成数据点z
meshc(x,y,z);%绘制曲面
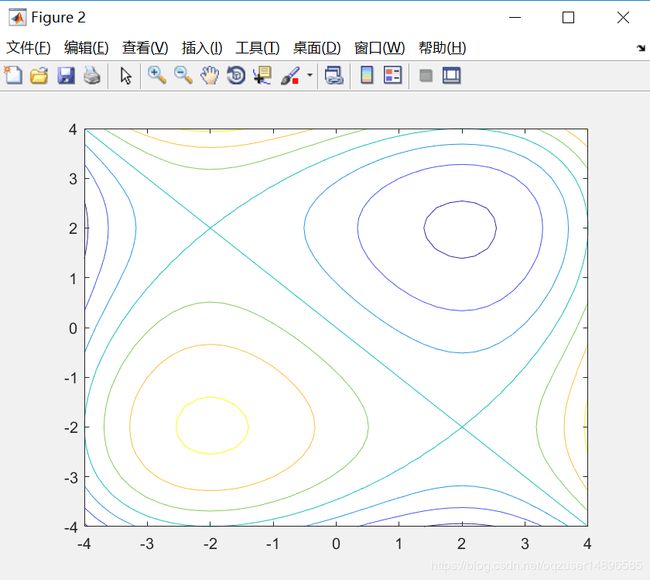
contour(z)

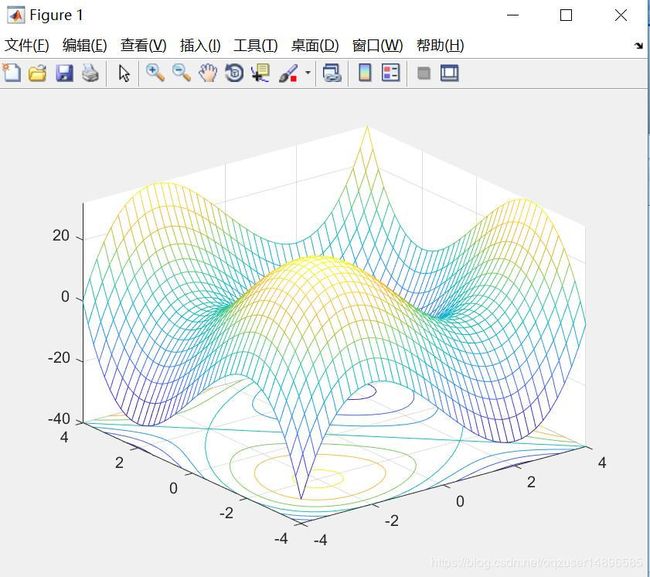
[x,y] = meshgrid(-4:0.2:4) %生成数据点并连成网格
z = x.^3+y.^3-12*x-12*y;%生成数据点z
meshc(x,y,z);%绘制曲面
[c,h]=contourf(z)%countourf填充颜色
clabel(c,h)%添加标注

[x,y] = meshgrid(-4:0.2:4) %生成数据点并连成网格
z = x.^3+y.^3-12*x-12*y;%生成数据点z
meshc(x,y,z);%绘制曲面
contour3(z,10)

还有教材51页画圆柱的例子，涉及到比较多的操作，有时间可以看下

教材48页，例题3.1.2，生成数据点z的时候在分母上加了一个eps，避免分母取到0值。

2.常微分方程求解

1.符号解

还记得解方程的solve命令吧？solve(Fun,x)方程原封不动抄进去，指出要求解的x。

dsolve也是这个道理，dsolve(‘eqn’,‘var’),eqn是常微分方程，原封不动抄进去，var是变量

以上是求通解的方法，求特解的方法就更容易了，直接在eqn后面添加condition（初始条件就可以了）

例题：求解下列常微分方程在给定初始条件下的特解

$y^{\prime \prime }=cos(2x)-y,y(0)=1,y^{\prime }(0)=0$

y = dsolve('D2y=cos(2*x)-y','y(0)=1','Dy(0)=0','x')
simplify(y)

2.数值解

求符号解要用表达式，求数值解要用function。

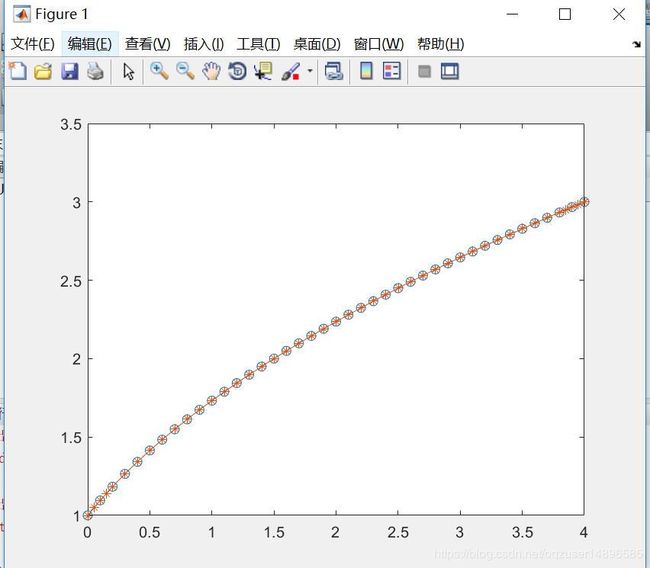
以ode45为例，与dsolve不同，参数要传进去函数句柄或者内联函数，这里直接用书上67页例3.4.4作为例题了

x=0:0.1:4;y=sqrt(1+2*x);
%odefun=inline('s-2*t/s','t','s') %生成内联函数
odefun =@(t,s)s-2*t/s %生成函数句柄
[t,s]=ode45(odefun,[0,4],1);
plot(x,y,'o-',t,s,'*-');

以上就是比较数值解和解析解的过程。

3.求解高阶微分方程

高阶微分方程式必须等价变化为一阶微分方程组，通过重新定义两个新变量。

这里直接讲书上的例3.4.5了，也可以直接看书，（手敲大括号太累了）

令$y_1=x,y_2=y_1^{\prime }$

则原微分方程变为方程组

$y_1^{\prime }=y_2,y_2^{\prime }=1000(1-y_1^2),y_2-y_1$

function dy = weifen1(t,y)
dy=zeros(2,1)
dy(1)=y(2)
dy(2)=1000*(1-y(1)^2*y(2)-y(1))

[T,Y] = ode15s('weifen1',[0 3000],[0 1])

此外，做出解的图形，也顺便看一下，在书上例3.4.4，3.4.5，3.4.6

---

3.线性代数实验

多项式不考，矩阵基本操作多且杂，复习的时候先看一遍，能记多少记多少，后面用的时候我会提的。所以这章我列举几个比较重要的操作，然后跳过矩阵部分，从最重要的求解线性方程组开始讲

1. 矩阵改变规模重新排列
2. 特殊矩阵的生成
3. 行列式
4. 删除某一特定行
5. 找出矩阵中大于x的元素
6. 求矩阵的迹
7. 提取上三角、下三角

1.求解线性方程组

复习一下线性代数的知识，如何判断一个线性方程组是否有解，有多少解？通过比较系数矩阵（A）的秩与增广矩阵（B）的秩可以得出结果。

直接上图了，如果r(A)!=r(B)，系数矩阵的秩与增广矩阵秩不同，无解，否则有解。

若r（A）=r（B）小于未知数个数n,那么有无穷多解，否则有唯一解。

简单的例题书上都有，先判断rank(A)和rank(B)的大小，之后根据情况判定有解还是无解，唯一解还是无穷解，下面讲一个综合一点的例子吧，做题之前先看一下书上95页练习4.4上面的总结！

例题：

syms lambda
A = [lambda 1 1;1 lambda 1;1 1 lambda];
b = [1;lambda;lambda^2];
D=det(A);
D=factor(D); %factor函数用来对符号多项式进行因式分解
%当 lambda != 1,-2的时候，有唯一解
r = rank(A);
x = A\b; %A始终在分母上，注意区分左除和右除
%当lambda = -2时，无解，求最小二乘解
lambda = -2;
A2 = eval(A);
b2 = eval(b);%将原矩阵中的lambda都赋值为-2，这就是eval函数的作用
r2A = rank(A2);
r2B = rank([A2,b2]);
B = rref([A2,b2]);%求出行最简型，观察到第三行应该删去，否则无法使用除法
B(3,:) = [];%删除第三行
x2 = B(:,1:3)\B(:,4);
%当lambda=1有无穷多解
lambda = 1;
A1 = eval(A);
b1 = eval(b);
r1A = rank(A1);
R2b = rank([A1,b1]);
X3 = null(A1,'r')%求齐次方程的通解
x
X3 = eval(x)%求齐次方程的特解
B = rref([A1,b1]);%求特解的替代方法
B(2:3,:) = [];
x3 = B(:,1:3)\B(:,4);

2.特征值和特征多项式

这一部分说简单也简单，说难也难。简单就是题目会很固定，掌握书上的步骤，照猫画虎就成了，难就难在，这节矩阵太多公式太多定理太多我打不过来…

emmm，所以我简单讲一个例子了，关于具体的原理，二次型正交变换之类的，有问题的当面问我吧

例题：P97页例4.5.3

源码如下：

A = [0,-1,1;-1,0,1;1,1,0];
[a,b] = eig(A);
P=orth(a)
B = P'*A*P
P*P'

简单解释一下我复习时遇到的问题吧

1. 什么是正交矩阵？

P’*P=E，转置与自身相乘（自身与转置相乘也满足）为单位矩阵，这样的矩阵就是正交矩阵。

2. 什么是正交变换？

如果P是正交矩阵，那么线性变换$y=Px$就成为正交变换。

这里有个性质还是提一下（与考试无关，可跳过）

假设$y=Px$是正交变换，则有$||x||=||y||$,什么意思呢？就是经过正交变换线段的长度保持不变！这是正交变换十分出色的特性。

3. 相似矩阵

设A,B都是n阶矩阵，若有可逆矩阵P，使得$P^{-1}AP=B$,那么称B是A的相似矩阵，对A进行$P^{-1}AP$运算成为对A进行相似变换

• 若n阶矩阵A与B相似，那么A与B特征多项式相同，特征值相同（一下把忘掉的线代都想起来了有没有~）

4. 对角化

对n阶矩阵A，寻求相似变换矩阵P，使得$P^{-1}AP=\Lambda$，称为把矩阵A对角化。

能够对角化的充要条件是，A有n个线性无关的特征向量。

5. 二次型化为标准型

贴一道我觉得比较清晰的例题：

这里面正交矩阵是在前一问求解的，我没放出来是因为不想解释了，反正在matlab里也是一条命令orth(a)的事儿，回忆整个二次型化为标准型的流程是我写这部分的主要目的。

好了总结一下把，如何求一个正交变换，把二次型化为标准型？

1. 输入矩阵A
2. [a,b] = eig(A),计算出A的特征值和特征向量，a是特征向量，我们接下来要用的
3. P=orth(a)，把特征向量正交化，题目到这里就结束了，很简单有没有，没有之前施密特正交化那么烦人。。。
4. 接下来就是验证工作了，需要验证正交化后的矩阵B=P’A*P,是一个对角阵
5. 还需要验证矩阵P是一个正交矩阵，对应命令不赘述了

---

4.最优生产方案

这是倒数第二个部分了，内容比较简单，放在前面做个放松吧。

这部分要点如下：

1. 线性规划和二次规划的标准形式，能够根据题目写出矩阵
2. 掌握linprog和quadprog命令
3. 注意quadprog中的H矩阵，标准形式中是$\frac{1}{2}{x}^{\prime }Hx$
4. 根据书上的例子，自己过一遍过程

---

5.概率论与数理统计实验

常见分布与命令字符

常见分布	二项分布	泊松分布	均匀分布	指数分布	正态分布	${\chi }^2$分布	t分布	F分布
命令字符	bino	poiss	unif	exp	norm	chi2	t	f

每种分布提供的五类函数以及命令字符

函数	概率密度函数	分布函数	分位数	均值与方差	随机数生成
命令字符	pdf	csf	inv	stat	rnd

1. 概率密度函数与分布函数的调用

2.分位数的调用

3.数据的描述与直方图

命令	名称
mean(x)	均值
median(x)	中位数
range(x)	极差
std(x)	标准差
var（x）	方差
[m,v ] = normstat(mu,sigma)	正态分布均值与方差
[m,v] = unifstat(a,b)	均匀分布的均值与方差
hist(x,n) 其中，n表示分为几段	直方图

4.参数估计

参数估计和下一节假设检验应该算是比较重要的两章了，是老师点名要出大题的

在MATLAB统计工具箱中，有专门计算总体均值、标准差的点估计和区间估计的程序，命令格式为：

[mu sigma muci sigmaci] = normfit(x,alpha)

其中，mu和sigma是总体均值$\mu$和标准差$\sigma$的点估计，后面两个是区间估计。

书上的例子也比较简单，都是先把数据敲进去，然后直接调用上面的方法。

5.假设检验中的计算

这一节主要分为三个部分，单个正态总体假设检验中的计算，双正态总体假设检验中的计算以及总体分布的正态性检验。主要内容如下：

主要看懂单正态总体假设检验整个的流程以及每个返回值的意义吧