Leetcode 51：N皇后（最详细的解法！！！）

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

上图为 8 皇后问题的一种解法。

给定一个整数 n，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个明确的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例:

输入: 4
输出: [
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]
解释: 4 皇后问题存在两个不同的解法。

解题思路

我们首先想到的解法是暴力解法，通过回溯法去解决这个问题，我们先看这样一个简单的例子。对于一个4x4的棋盘。如果我们的第一步放在

接着我们要往第二行上放，这就不能放在这两个位置。

这实际上是一种剪枝行为。最后，我们将第二个皇后放在

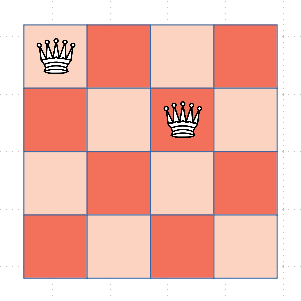
接着，我们考虑第三个皇后的位置，我们发现此时，第三个皇后没有位置可以放了。所以我们将第二个皇后，移动到下一个可行位置，然后我们放入第三个皇后

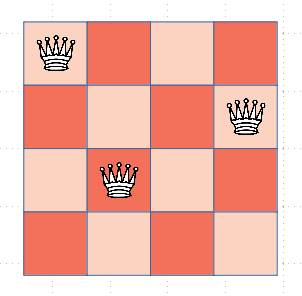
接着我们放入第四个皇后，我们发现第四个皇后没有位置可以放了，而第三个和第二个皇后也没有可行位置了，我们就调整第一个皇后的位置，最后我们可以得到这样两个可行解。

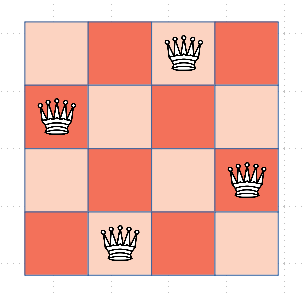
我们现在就要思考怎么通过编程去解决放的位置是否合法这个问题。也就是我们要解决，横向竖向的坐标表示，以及两个斜线方向的坐标表示。横向竖向很简单

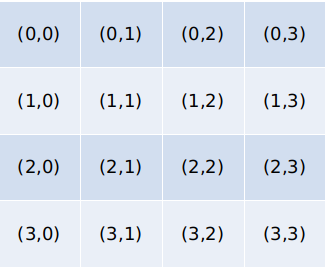
我们通过简单的坐标表示就可以确定两个点是不是在同一个横向和竖向上。那么斜线方向呢？我们将x+y

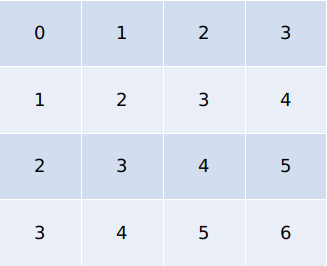
相信你也看出规律来了y=x这个斜线方向，可以通过x+y表示。我们再将x-y

为了避免出现负数，所以我们将这个矩阵加上一个常数n-1，就变成了

我们可以将y=-x上的斜线，通过x-y+n-1表示出来。这样我们就解决了最核心的问题，依照前面的解题思想，我们很容易写出这样的代码

class Solution:
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        col = [0 for i in range(n)]
        dia1 = [0 for i in range(2*n - 1)]
        dia2 = [0 for i in range(2*n - 1)]

        def generateBoard(row):
            board = [str() for i in range(n)]           
            for i in range(n):
                board[i] = row[i]*'.' + 'Q' + '.'*(n - row[i] - 1)

            return board

        result = list()
        def putQueen(index, row):
            if index == n:
                result.append(generateBoard(row))
                return

            for i in range(n):
                if not (col[i] or dia1[index + i] or dia2[index - i + n - 1]):
                    row.append(i)
                    col[i], dia1[index + i], dia2[index - i + n - 1] = 1, 1, 1
                    putQueen(index + 1, row)
                    col[i], dia1[index + i], dia2[index - i + n - 1] = 0, 0, 0
                    row.pop()

        putQueen(0, list())
        return result

我们能不能通过迭代去解决这个问题呢？也是可以的。我们不想在迭代中，再通过记录不同的变量的形式去判断我们放入的皇后是否满足条件，有没有什么更好的策略呢？其实我们观察皇后摆放的位置就可以发现这样的规律

• 考虑第n行皇后的摆放位置，对于之前的所有行i要满足：row[i] != row[n] and abs(row[i] - row[n] )!=abs(i - n)

class Solution:
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        result = list()
        row = [0 for i in range(n)]
        def generateBoard(m, row):
            board = [str() for i in range(n)]           
            for i in range(m):
                board[i] = row[i]*'.' + 'Q' + '.'*(m - row[i] - 1)

            return board

        def isValid(k, row):
            for i in range(k):
                if row[i] == row[k] or abs(row[i] - row[k]) == abs(i - k):
                    return 0
            
            return 1

        k = 0
        while k >= 0:
            while row[k] < n and not isValid(k, row):
                row[k] += 1

            if row[k] < n:
                if k == n - 1:
                    result.append(generateBoard(n, row))
                    row[k] += 1
                else:
                    k += 1
            else:
                row[k] = 0
                k -= 1
                row[k] += 1

        return result

实际上这个问题和之前的Leetcode 46：全排列（最详细的解法！！！） 很类似。这个问题有一个非常简洁的写法。你观察这个问题的解，你会发现这些解实际上是有规律的，有什么规律？所有解都是range(n)全排列的子集。也就是我们可以通过遍历这个全排列集合去寻找到它们。那么什么样的子集才满足解的条件呢？只要满足这两个条件

• 解k中的第i个元素减去i组成的集合大小为n
• 解k中的第i个元素加上i组成的集合大小为n

注意，我这里指的解是row，对于4x4问题，也就是[1,3,0,2]和[2,0,3,1]这两个解。

import itertools
class Solution:
    def solveNQueens(self, n):
        """
        :type n: int
        :rtype: List[List[str]]
        """
        result = list()
        for permute in itertools.permutations(range(n)):
            if len(set(i + v for i, v in enumerate(permute))) == n and \
                len(set(i - v for i, v in enumerate(permute))) == n:
                result.append(['.'*v + 'Q' + '.'*(n - v - 1) for v in permute])

        return result

但是实际上上面的解法将所有结果穷举了出来，显然速度很慢。

我将该问题的其他语言版本添加到了我的GitHub Leetcode

如有问题，希望大家指出！！！