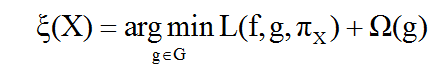与模型无关的局部可解释性方法(LIME)
在机器学习模型事后局部可解释性研究中,一种代表性方法是由Marco Tulio Ribeiro等人提出的Local Interpretable Model-Agnostic Explanation(LIME)。
一般地,对于每一个输入实例,LIME首先利用该实例以及该实例的一组近邻数据训练一个易于解释的线性模型来拟合待解释模型的局部边界,然后基于该线性模型解释待解释模型针对该实例的决策依据,其中,线性模型的权重系数直接体现了当前决策中该实例的每一维特征重要性。
LIME方法希望达到可解释性和局部可信度之间的平衡:
其中:
f:机器学习模型(待解释模型);
g:可解释模型(简单模型,如线性回归、决策树等);
G:可解释模型集合;
:可解释模型的复杂度度量(决策树是树的深度,线性模型是非零系数的个数等),在求解时应尽量小;
X:输入实例的特征;
:相似度度量函数;
L:损失函数,表征可解释模型g和复杂模型f在X附近的不一致程度;在求解时应最小化;
:目标函数。
上式中,输入是一个样本点X,输出是一个简单的可解释模型g,该可解释模型g需满足以下条件:
1.简单模型g的复杂度尽量小,即 尽量低,以求得g的可解释良好;
2.简单模型g在输入样本X附近与复杂模型f的预测效果尽量相同,即针对与X越近(或相似度越高)的样本,g与f的预测值应尽量一致,以保证g在局部能很好地近似f。
通过以上限制条件,寻求g的可解释性和g在局部近似f的可信度之间的平衡。
具体步骤:
步骤1
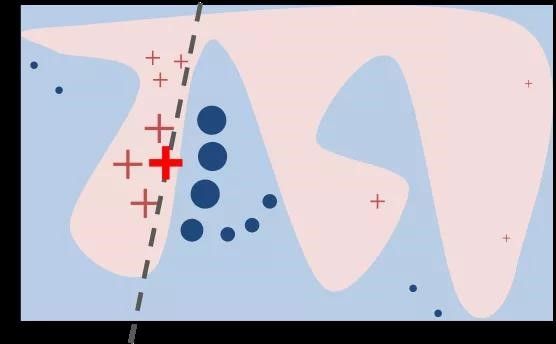
选用复杂模型f(如深度神经网络等)在全体数据上进行训练拟合;上图中,蓝色和粉色区域的边界是复杂模型的决策边界。可以看到,在全局范围内,原模型的决策边界十分复杂,但并不妨碍在局部可以使用简单模型g(如线性模型)对复杂模型进行近似拟合。
步骤2
图中,粗体红色叉点代表一个输入示例X,我们想知道复杂模型对该样本进行预测时所依据的特征重要性或者是更看重哪些特征,在此之前需要用一种可解释的表示方法对样本数据进行表示。
可解释性数据表示,旨在用一种人类可理解的表示方法对样本数据进行表示,而不考虑模型实际使用的是什么样的样本表示。
例如,在文本分类中,对于一条输入样本的可解释性表示,可能是与原样本长度相同的二进制向量,在对该样本进行扰动取样后,若所得样本对应位置的词若相对于原输入样本做了改变,则其二进制向量表示的对应位置取反,以表征原样本中的词不存在;若所得样本对应位置的词若相对于原输入样本没有改变,则其二进制向量表示的对应位置不变,以表征原样本中的词依然存在。如原样本“我喜欢这部电影”分词后(我,喜欢,这,部,电影)的可解释性表示为[1,1,1,1,1],经过扰动取样后得到“他喜欢这部电影”、“我喜欢那部电影”、“我讨厌这部电影”,对应的可解释性表示分别[0,1,1,1,1]、[1,1,0,1,1]、[1,0,1,1,1]。在使用简单模型拟合近似原复杂模型时,就是使用类似于这种人类可理解的表示方法来表示样本。
步骤3
通过扰动取样,得到粗体红色叉点附近的样本点X′,并用原有的复杂模型对它们进行预测分类。从图中可以看到,一部分样本被预测为叉点类,另一部分是圆点类。
注意:在选定的输入样例X周围,需要进行多次扰动生成局部样本,以供简单的可解释性模型学习拟合。在数据扰动时,不能作随机且无意义的扰动。对于图像数据,按照超像素(可理解的图像块)变更;对于文本数据,对单个词逐一扰动;对于结构化数据,每次单独改变一个特征。
步骤4
定义一个相似度度量函数 ,衡量抽取的样本点X′与原样本点X(粗体红色叉点)之间的距离(或相似度),并作为这些扰动样本点的权重。从图中可以看到,与原样本点距离越近,则样本点越大,距离越远则越小。
因为简单模型需要在输入样本X的附近很好地近似复杂模型,所以对与X距离越近的样本,所给予的重视度要越高。因此,需要相似度函数赋予各扰动样本相应的权重,以便使用简单模型在这些样本上训练时,同时考虑到这些样本的重要性,以确保简单模型对与X越近的样本拟合程度越好,因而越能很好地近似复杂模型在X附近(局部)的行为。
步骤5
在这些附带权重的样本点X′上(包括原样本点X),选取简单的线性模型进行训练拟合,则可以得到一个在原样本点X附近(局部)可以近似复杂模型的简单线性模型,从而得到线性模型中各特征的权重,据此得知原来的复杂模型在预测样本X时,更看重X的哪些特征。
在LIME提出时,多采用线性模型作为可解释性的简单模型,在输入样本点的局部近似拟合复杂模型。由于自身附带良好可解释性的模型还有决策树、逻辑回归、贝叶斯网络等,因而可以考虑采用不同的简单模型作为原复杂模型的局部近似模型。