hdu 5726 GCD 解题报告

Give you a sequence of N(N≤100,000) integers : a1,...,an(0<ai≤1000,000,000). There are Q(Q≤100,000) queries. For each query l,r you have to calculate gcd(al,,al+1,...,ar) and count the number of pairs (l′,r′)(1≤l<r≤N)such that gcd(al′,al′+1,...,ar′) equal gcd(al,al+1,...,ar)

.

Input The first line of input contains a number T, which stands for the number of test cases you need to solve.

The first line of each case contains a number N, denoting the number of integers.

The second line contains N integers, a1,...,an(0<ai≤1000,000,000).

The third line contains a number Q, denoting the number of queries.

For the next Q lines, i-th line contains two number , stand for the li,ri, stand for the i-th queries.
Output For each case, you need to output “Case #:t” at the beginning.(with quotes, t means the number of the test case, begin from 1).

For each query, you need to output the two numbers in a line. The first number stands for gcd(al,al+1,...,ar) and the second number stands for the number of pairs (l′,r′) such that gcd(al′,al′+1,...,ar′) equal gcd(al,al+1,...,ar).
Sample Input

1
5
1 2 4 6 7
4
1 5
2 4
3 4
4 4

Sample Output

Give you a sequence of N(N≤100,000) integers : a1,...,an(0<ai≤1000,000,000). There are Q(Q≤100,000) queries. For each query l,r you have to calculate gcd(al,,al+1,...,ar) and count the number of pairs(l′,r′)(1≤l<r≤N)such that gcd(al′,al′+1,...,ar′) equal gcd(al,al+1,...,ar)

.

Input The first line of input contains a number T, which stands for the number of test cases you need to solve.

The first line of each case contains a number N, denoting the number of integers.

The second line contains N integers, a1,...,an(0<ai≤1000,000,000).

The third line contains a number Q, denoting the number of queries.

For the next Q lines, i-th line contains two number , stand for the li,ri, stand for the i-th queries.
Output For each case, you need to output “Case #:t” at the beginning.(with quotes, t means the number of the test case, begin from 1).

For each query, you need to output the two numbers in a line. The first number stands for gcd(al,al+1,...,ar) and the second number stands for the number of pairs (l′,r′) such that gcd(al′,al′+1,...,ar′) equal gcd(al,al+1,...,ar).
Sample Input

1
5
1 2 4 6 7
4
1 5
2 4
3 4
4 4

Sample Output

Case #1:
1 8
2 4
2 4
6 1

题意：

给你n个数字，现在问你q次L,R区间的gcd值以及有多少个区间的gcd值和L，R相等（L，R本身也算一个）

思路：

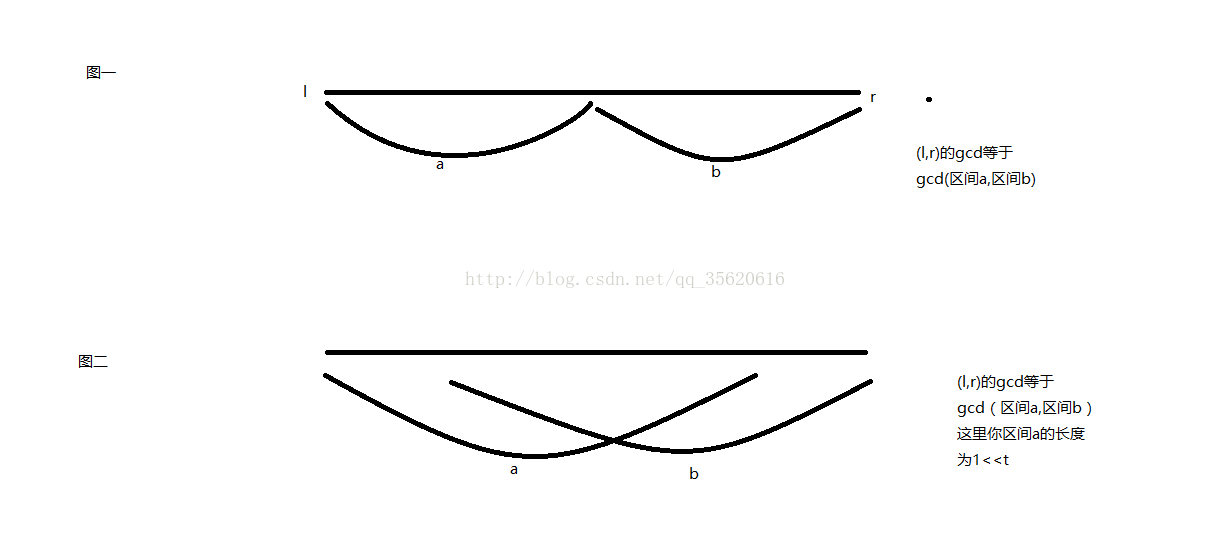
先用rmq预处理计算任意区间的gcd值；然后计算和该区间gcd相等的区间有多少个，代码如下：

#include //建议从主函数开始看
using namespace std;
#define LL long long
const int maxn = 100005;
int dp[maxn][20];//dp[i][j]代表从第i位开始往后(1<m;//m[i]代表gcd值为i的区间有多少个

int main(){
    int test;
    scanf("%d",&test);
    int T=0;
    while(test--){
        T++;
        m.clear();
        scanf("%d",&n);
        for(int i=1;i<=n;i++)scanf("%d",&num[i]);
        init();
        for(int i=1;i<=n;i++){//这里统计各区间的gcd值
            int l=i,r=i;//当你计算l,r的区间gcd值时随着r的增加这个值一定是递减的，所以我们可以这样计算：
//首先枚举i端点，然后二分找到一个最右边的r使区间(l,r)的gcd等于(l,l)，也就是说此时(l,r+1)是一个比之前小的gcd值，再如法炮制从(l,r+1)找有多少个和（l,r+1）
//gcd值相等的区间，由于不知道什么鬼的证明说对于一个端点i最多能找出来log2(n)个gcd值，而每次找的复杂度为log2(n),所以这里整体复杂度为n*logn*logn;
       while(r<=n){
                int ll=r;
                int rr=n;
                int v=rmq(l,r);
                while(ll<=rr){//二分找有多少个区间gcd等于(l,r)
                    int mid=(rr+ll)/2;
                    if(rmq(l,mid)>=v)ll=mid+1;
                    else rr=mid-1;
                }
                m[v]+=ll-r;
                r=ll;//更新r,这样可以继续找
            }
        }
        int q;
        scanf("%d",&q);
        printf("Case #%d:\n",T);
        while(q--){
            int L,R;
            scanf("%d%d",&L,&R);
            int ans=rmq(L,R);
            printf("%d %lld\n",ans,m[ans]);
        }
    }
}