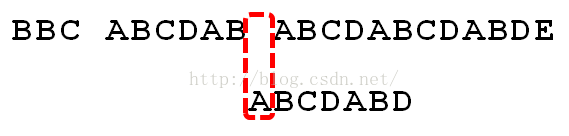KMP算法讲解(next数组求解)
KMP算法
关于算法部分,网上有比较多写的好的博客了,下面是我看到的一篇。https://blog.csdn.net/liu88010988/article/details/50789960
这种算法不太容易理解,网上有很多解释,但读起来都很费劲。直到读到Jake Boxer的文章,我才真正理解这种算法。下面,我用自己的语言,试图写一篇比较好懂的KMP算法解释。
1.
首先,字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。
2.
因为B与A不匹配,搜索词再往后移。
3.
就这样,直到字符串有一个字符,与搜索词的第一个字符相同为止。
4.
接着比较字符串和搜索词的下一个字符,还是相同。
5.
直到字符串有一个字符,与搜索词对应的字符不相同为止。
6.
这时,最自然的反应是,将搜索词整个后移一位,再从头逐个比较。这样做虽然可行,但是效率很差,因为你要把"搜索位置"移到已经比较过的位置,重比一遍。
7.
一个基本事实是,当空格与D不匹配时,你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是,设法利用这个已知信息,不要把"搜索位置"移回已经比较过的位置,继续把它向后移,这样就提高了效率。
8.
怎么做到这一点呢?可以针对搜索词,算出一张《部分匹配表》(Partial Match Table)。这张表是如何产生的,后面再介绍,这里只要会用就可以了。
9.
已知空格与D不匹配时,前面六个字符"ABCDAB"是匹配的。查表可知,最后一个匹配字符B对应的"部分匹配值"为2,因此按照下面的公式算出向后移动的位数:
移动位数 = 已匹配的字符数 - 对应的部分匹配值
因为 6 - 2 等于4,所以将搜索词向后移动4位。
10.
因为空格与C不匹配,搜索词还要继续往后移。这时,已匹配的字符数为2("AB"),对应的"部分匹配值"为0。所以,移动位数 = 2 - 0,结果为 2,于是将搜索词向后移2位。
11.
因为空格与A不匹配,继续后移一位。
12.
逐位比较,直到发现C与D不匹配。于是,移动位数 = 6 - 2,继续将搜索词向后移动4位。
13.
逐位比较,直到搜索词的最后一位,发现完全匹配,于是搜索完成。如果还要继续搜索(即找出全部匹配),移动位数 = 7 - 0,再将搜索词向后移动7位,这里就不再重复了。
14.
下面介绍《部分匹配表》是如何产生的。
首先,要了解两个概念:"前缀"和"后缀"。 "前缀"指除了最后一个字符以外,一个字符串的全部头部组合;"后缀"指除了第一个字符以外,一个字符串的全部尾部组合。
15.
"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例,
- "A"的前缀和后缀都为空集,共有元素的长度为0;
- "AB"的前缀为[A],后缀为[B],共有元素的长度为0;
- "ABC"的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
- "ABCD"的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
- "ABCDA"的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为"A",长度为1;
- "ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为"AB",长度为2;
- "ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB],后缀为[BCDABD, CDABD, DABD, ABD, BD, D],共有元素的长度为0。
16.
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。
分割线
KMP中的关键就是求公共最长匹配前缀和后缀的长度了(多读几遍这句话 你就懂了),不过下面的代码里面采取的方式和上述已经匹配长度-部分匹配值有点不太一样,直接求了next[]数组,一般KMP要么是通过前者,要么是通过后者这种方式来讲解的。
next[]数组定义
next[]数组的定义,这里先给出数学形式化的描述,可能有点抽象,不过没事,记住,一切能用数学公式或字母来形式化的东西,都是为了辅助我们更好的表述,它是无二义的,请不要害怕它。
n e x t [ j ] = { − 1 , j = 0 m a x { k ∣ 1 ≤ k ≤ j 且 t [ 0 ] . . . t [ k − 1 ] = t [ j − k ] . . . t [ j − 1 ] } , 集 合 非 空 0 , 其 他 情 况 next[j]=\begin{cases} -1,\quad j=0 \\ max\{k | 1\le k\le j 且 t[0]...t[k-1]=t[j-k]...t[j-1]\}, \quad 集合非空 \\ 0,\quad 其他情况 \end{cases} next[j]=⎩⎪⎨⎪⎧−1,j=0max{k∣1≤k≤j且t[0]...t[k−1]=t[j−k]...t[j−1]},集合非空0,其他情况
next[j]就是待匹配串从t[0]开始到t[j-1]结尾的这个子串中,前缀和后缀相等时对应前缀/后缀的最大长度,请看下图,j=10(下标从0开始):

那么,next[j]即next[10]就是待匹配串从t[0]开始到t[9]结尾的这个子串(即aabcaabcaa)中,它的前缀有很多,后缀也有很多,前缀和后缀对应相等的也有一些,不过长度最大的那个是aabcaa子串,所以next[j]=6,注意一下,我们定义next[0]=-1,因为这个时候t[0]到t[j-1]这个子串是不存在的,请注意和next[j]=0的意义区分一下。
至于说next[j]=0的情况嘛,你可以考虑一下这种情况,这个时候t[0]到t[j-1]这个子串是存在的,但是前缀和后缀相等的序列是不存在的:

#include
using namespace std;
#define MAX_LEN 100
/*
* 求待匹配串的next数组
*/
void get_next_arr(char* t, int* next)
{
// next[i]的求解方法是,找到从t[0]~t[i-1]的公共最长匹配前缀和后缀的长度
next[0]=-1; // next[0]定义为-1
next[1]=0; // next[1]肯定是0
// 只要待匹配串还没到底,都要求相应位的next[i]值
for (int i = 2;t[i] != '\0';i++)
{
int max_len=i-1; // 最长长度为i-1
int len,j;
for (len = max_len;len >= 1;len--) // 从最长的情况开始搜索
{
for (j = 0;j < len;j++)
{
if(t[j]!=t[j+i-len]) // 只要有任何一位不对应相等,那么当前len就不成立,试探下一个len
break;
}
// 如果上一个循环是正常退出,即都对应相等了,那就把当前的len赋给next[i],并不再往下试探了
if(j==len)
{
next[i]=len;
break;
}
}
if (len < 1) // 如果len=1的情况都不成立,那next[i]肯定是0了
{
next[i]=0;
}
}
}
int KMP_match(char* s, char* t)
{
// 先求待匹配串的next集合
int next[MAX_LEN];
get_next_arr(t, next);
// 再开始匹配,匹配时,在搜索串中的下标不回溯,在待匹配串中的下标根据下标j和对应的next[j]进行回溯
int i=0,j=0;
while (s[i]!='\0'&&t[j] != '\0')
{
if (s[i] == t[j]) // 如果匹配,继续往下搜索
{
i++;
j++;
}
// 否则的话,更新索引j
else
{
j = next[j];
// 注意处理一下-1的情况
if (-1 == j)
{
i++;
j++;
}
}
}
if (t[j] == '\0') // 如果匹配到了最后,那就是匹配成功,返回串首的下标
return i-strlen(t);
else // 否则返回-1
return -1;
}
int main()
{
char* s="abcdabbcdabcdabd";
char* t="abcdabd";
cout< 二更
细心看了代码的朋友可能会发现,在上面的求next[]数组的代码中,我采用的是简单的暴力搜索的方式,即对于各个next[i],代码都会去搜索t[0]~t[i-1]这个子串的所有长度的前缀和后缀,找的时候从最长的可能开始找起,一旦找到就将这个长度赋给next[i]。简单从代码上来看,有3个for循环,自然复杂度为 O ( m 3 ) O(m^3) O(m3),m指的是待匹配串的长度。一般来说,待匹配串的长度m都是比较小的,不过,肯定有更好的算法去避开这个 O ( m 3 ) O(m^3) O(m3),最好结果是 O ( m ) O(m) O(m),下面开始讲解,我会画一些图来辅助理解。
读到这里,请务必回顾一下next[]数组的定义。
请看下面的例子:

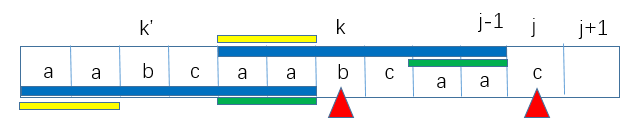
现在我们知道了next[j]=6,那么怎么求next[j+1]呢?且看下面的分析过程:
既然next[j]=6,这里我们记next[j]=k,在上图中,k对应等于6,也就是说 t [ 0 ] . . . t [ k − 1 ] t[0] ... t[k-1] t[0]...t[k−1]和 t [ j − k ] . . . t [ j − 1 ] t[j-k] ... t[j-1] t[j−k]...t[j−1]是对应相等的,也就是图上的两个蓝色条。
好,现在我们注意到,t[j]=t[k],也就是说,如果我们在两个蓝条后面都加一个相等的字符,那肯定也是对应相等的,这种情况最简单了,此时next[j+1]=next[j]+1。
我们再考虑t[j]≠t[k]的情况:

好,既然你两个蓝色条对应相等,那我取其中的一部分,那也肯定是对应相等的,没毛病,我就取下图中绿色这两段:

选取的依据就是next[k]的大小了,我们记next[k]=k’,于是下面的等式成立:
t [ k − n e x t [ k ] ] . . . t [ k − 1 ] = t [ j − n e x t [ k ] ] . . . t [ j − 1 ] t[k-next[k]] ... t[k-1]=t[j-next[k]] ... t[j-1] t[k−next[k]]...t[k−1]=t[j−next[k]]...t[j−1]
又根据next[k]的定义,我们可以得到下面的等式:
t [ 0 ] . . . t [ n e x t [ k ] − 1 ] = t [ k − n e x t [ k ] ] . . . t [ k − 1 ] t[0] ... t[next[k]-1]=t[k-next[k]] ... t[k-1] t[0]...t[next[k]−1]=t[k−next[k]]...t[k−1]
上述两个等量代换,得到
t [ 0 ] . . . t [ n e x t [ k ] − 1 ] = t [ j − n e x t [ k ] ] . . . t [ j − 1 ] t[0] ... t[next[k]-1]=t[j-next[k]] ... t[j-1] t[0]...t[next[k]−1]=t[j−next[k]]...t[j−1]
也就是说,下图中①号对应的黄色条子串和②号对应的绿色条子串是对应相等的:

那么,我们现在只要比较t[j]和t[k’](注意,这里是k’),也就是图中两个紫色的三角形,如果t[j]=t[k’],好办,next[j+1]=k’+1;如果t[j]≠t[k’],额,你还记得我们这种情况下是怎么进来的吗?不就是t[j]≠t[k]嘛!现在又来个t[j]≠t[k’],而k’=next[k],自然而然就会想到递归处理了,事实上,它们之间的确满足这个递归。至于递归退出的条件,就是next[0]这个边界值了。
next[]数组的递归求解
/*
* 求待匹配串的next数组,递归求解
*/
void get_next_arr_2(char* t, int* next)
{
next[0] = -1; // next[0]定义为-1
next[1] = 0; // next[1]肯定是0
int k;
for (int j = 2;t[j] != '\0';j++)
{
k=next[j-1];
if (k == -1)
{
next[j]=0;
continue;
}
else
{
while (t[j-1] != t[k] && k!=-1)
k=next[k];
if(t[j-1] == t[k])
next[j]=k+1;
else
next[j] = 0;
}
}
}
写的不对的地方,还请指出