python实现货币贷款分期计算（等额本金/等额本息）

背景

    最近要开始投身研究（互联网）金融了，加上最近借了一个朋友3万块钱，因为他之前是在互联网平台（某吱）上借，大概万三(10k一天3元的费用)的日息(年化差不多有11%了，速算0.0003*360=0.108)，于是便一拍即合我便按照7%的年化借了30k给他，后又商定按期限半年六次月分期来还。

    借款发生在6月5日，鉴于朋友他的公司是10号发薪，考虑服务要周到，要等用户有工资了才有钱还，那么还款日定在7月10日开始至12月10日还满6次。最终结果则是：每月还款5107.52，最终一共还款30645。

   这里有些自己总结的相关速算：

          1.一共多还约为本金的2.15%（645/30000=0.0215）；

          2.和这样算是接近的：年化（7%）的半年要除2即为3.5%，然后因为是近线性还款所以款在手中的积分大概是全款在手的0.5（实际比一半的时间要多），则是3.5%/2=1.75%（2.15%比1.75%会多一点）

介绍

关于等额本金/等额本息，自行百度/wiki了解，读读代码和注释其实也理解不难。此类一般复利的计算周期是月，也就是每月刷新本金池计算一遍利息。

 新浪: 房贷等额本金/等额本息哪个更合适

上代码正文

   阅读以下代码时，需要了解基本的python面向对象编程，以及等额本金/等额本息的大致概念。

   这段代码还有一个非常好的功能，就是可以考虑第一个还款周期不是一个标准定义周期(一般是月)的情况，比如背景那个例子的"考虑服务要周到"特性，关键参数为first_period_rate。按照经验银行贷款会经常有这样的情形（银行一般考虑结算管理，而实际的放款日可以是一个月中的任意时间）。当不考虑该情况或借款生效日到第一个还款日一定一个标准周期时，该参数默认为1.0。很有服务意识也非常之实用：

# ===========================================
# @Time    : 2019/7/2 15:37
# @project : MLprocess
# @Author  : antony
# @Email   : [email protected]
# @File    : Installment
# @Software: PyCharm
# ===========================================

from sympy import solve
from sympy import abc


class MonthInstallment:
    """
    按月的分期付款计算，按月息为计息周期，一般常用的方式有等额本金和等额本息
    """
    def __init__(self, corpus, periods, y_rate, first_period_rate=1.0):
        """
        .   @param corpus 本金.
        .   @param periods 期数 即还款一共分期几个月.
        .   @param y_rate 年化利率 我们一般以年化来讨论.
        .   @param first_period_rate 第一个周期月的倍率，恰好为整月时是1.
        """
        self.m_rate = y_rate/12                          # 月利率
        self.corpus = corpus                             # 本金
        self.periods = periods                           # 期数
        self.first_period_rate = first_period_rate       # 第一周期月的倍率
        self.m_corpus_return = corpus/periods            # 每期应还本金
        self.return_li = []                              # 应还列表


    def equal_corpus(self):
        """
        等额本金
        """
        return_interest_li, left_ = [], self.corpus
        for i in range(self.periods):
            return_interest_li += [left_ * self.m_rate]  # 每期对应的利息，注意等额本金是每期都把利息还完了
            left_ -= self.m_corpus_return                # 剩余应还本息，相当于只考虑本金部分每期应还的部分
        return_interest_li[0] *= self.first_period_rate  # 对第一个月的应还利息做first_period_rate的修正
        self.return_li = [x + self.m_corpus_return for x in return_interest_li]
        return self.return_li

    def equal_corpus_interest(self):
        """
        等额本息，比较常用，似乎是贷款的默认计算方式，无论银行还是网贷主要应用等额本息
        """
        left_ = self.corpus * (1 + self.m_rate) ** self.first_period_rate - abc.x  # 剩余应还本息，这里先计算第一个月
        for i in range(1, self.periods):
            left_ = left_ * (1 + self.m_rate) - abc.x  # abc.x为未知数：每月应还金额，注意到等额本息每期金额是一样的
        return_x = solve(left_, [abc.x])  # 解方程剩余应还金额为0，求得未知数abc.x
        self.return_li = [return_x[0] for x in range(self.periods)]
        return self.return_li


if __name__ == '__main__':
    print(__name__)
    # from mark_finance.loanp2p.Installment import *
    mo = MonthInstallment(30000,6,0.07,1.13)
    mo.equal_corpus()

欢迎关注我的github对应部分代码，后面有关互金的好用的东西还会补充到其中。因为主要实现计算，所以以下是一些不那么好看的结果和应用，还没有做相应可读性更强的格式化输出。

结果1，以背景为例：

     由于首月到还款日是经历了35天，所以first_period_rate应该传入35/30，年化0.07(函数内会转化成月息)，分期6次，那么两种方式分别的还款为：

可以看出都是半年多还了640多块钱，几乎没什么区别，虽然等额本金趋向于“更早地去还了更多的钱”，不过时间太短几乎没区别。

此处有个金融概念：复利终值。

结果2，一个买房贷款案例：

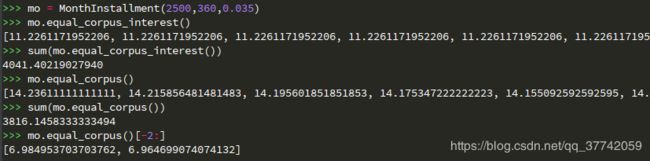
    假设帅君贷款250w=2500k买房（那么我们下面输入时2500的单位即为千元），我们分别假定他贷款20年(240期)，30年(360月)，贷款利率分别3.5%和5%：

以上是年化3.5%来计算的，这相当于大概公积金贷款的利率，最终都一共还了3479k和3378k，可以心算下是原始本金的多少倍，此时也可以直接把本金都变成1来分别看倍数。

等额本息每个月都是相同的14.5k左右，等额本金就是越还越少，最后俩月（取输出数组的最后两个元素）可以看到只有10.4k左右啦：

事实上此数值会十分接近一期份儿的本金（很好理解，每期把截止到那时的利息部分都还了，到了最后几乎没剩什么利息，只剩约对应一期的本金）。

       这里可以看出年限长了之后，看起来等额本金还的复利终值是少了一些，但其实不然，借用朋友的一句话“这个其实利息固定，其它怎么算都一样，只是看起来少了，但是钱的使用期限也少了”，道理应该都懂。

那么同样利率的30年呢：

    这里可以用一种大概的速算看到一个事实，来对比等额本息，年化3.5%的30年是共105%的息；但由于钱和时间算积分只有略大于一半的全额30年的样子，那么息即为略大于52.5%（但如果考虑一定程度的通货膨胀，那就不是略大了，虽然等额本息的余额是线性的但越早的膨胀率越小，即越值钱），而我们最后看到等额本息约是61.64%（4041/2500=1.6164），好像也确实大了一点，但比略微感觉应该还是多了一点的，这大概就是复利的影响了，毕竟复利周期是月，而上面的速算基本是只计算一次利息来看。

     这里的比较其实都是没有考虑通货膨胀的（上文括号里的部分），参考过去几十年的通货膨胀，考虑进去的话其实这样的贷款应该还是挺划算的，公积金贷款简直可以看做是种福利，即便是5%左右年化的商业贷款应该也还是很划算。

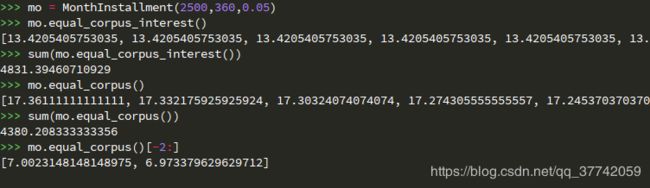
那么如果是5%的年化是怎样呢：

      可以看到第三个参数年化利率是0.05了；同样可以进行上一节类似的速算，结论应该差不多。

             速算：30年的5%的一半略多=>150%*略多于0.5=>略多于75%；
             实际：93.25%（4831.39/2500=1.932556）； 比上例3.5%同样30年的落差还是稍微大些的。

      不过能依稀感受到的是利息越高对复利的影响就稍稍更大一些，这估计也构成了此状况““”高利率的借钱容易让人陷入其中，甚至很多人后面连利息都还不上“””的原因之一吧。

      另外：对比最后两种情形的等额本金还款列表的最后两个月，可以看出，等额本金到最后几乎是剩不下多少利息了，事实上每次还款都是还干净利息了的，所以只要期数一样，那么它们的最后一个月金额都是接近于一份本金的数值，即6.9k多一点点的样子(2500/360=6.9444444)。

-----------------------------------------------------------------------------------------------------------------------------------------------------------------------------

写在最后

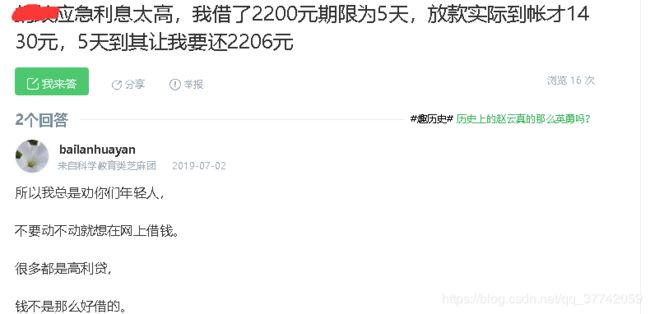
    年轻人，还是少去网贷，即便真要贷也不能随意就网贷，常常就会有在你的预期之外的情况出现，like：

     这里不针对平台，这里面的内容还是挺杂的（比如除了利息之外还有各类其他费用），空子还是挺多的，水还是挺深的，以及不明确的费用/复利计算方式，以及逾期计算。然后了解下行内比较厉害和夸张的比如什么714高炮这些的操作，比如贷款得到的钱直接砍去头息，操作贼多，所以真的非要网贷，也还是得去找些大点的靠谱点的平台，并且还是得仔细研究协议，成本还是非常之高的。当然，当你踏足进来遇到的很多情况即便是月分期的账单，可能也不太适用于上述类MonthInstallment的两个计算方法了；所谓预期之外。想想曾经还在读书的我以为："高出银行存款利息5倍的为高利贷"，简直是太简单了啊，现在看来即便按照存款利息能到年化4%(基本完全碾压国债和货币基金)，以上论断还都是显得太简单了；实际不规范的放贷更是能超过100%。
     现在的这块市场总的来说还是给人一些信任缺乏的感觉，“借款人怕不平等条约，放款人怕老赖”。金融（相关）行业利益很多，也是基于这个原因，即便不信任，其中的各位角色依然有利可图，那么自然会有不少的受害人。越是不规范，这块的空间其实也就越大。虽然，相关治理也总是慢慢在路上的。

    但是，刚了解到实际有借钱这种需求并且找到这样相关渠道的人群，和能读到我的文章的人群，画像其实是差别简直不要太大，反正是非常之大的，所以"写在最后"其实写了跟没写一样，多的还是得靠其他渠道的意识普及。

    或许，也是在了解了这些之后才觉得，房贷真的算是贷款中很趋近于“简直是福利了”的，尤其是你是公积金做的房贷。

    补充在后面的经历，后来没过多久(大概一个月)，我便离开了那里，大概是因为做的事情多少有些不太喜欢，提离职的那天，正好遭到了公安抽查，虽然场面很大，但其实打心底觉得应该不会有什么，如今又正在做一件稍微更喜欢的事情，中二台词：“算法可能能真正发挥它保护这个世界的公正的，没有骗局的，更和谐的事情”。又是一个多月过去了，听到那边裁员70%的消息，估计产品是要下线的节奏吧，我不知道该说些什么，“这事与我无瓜”？不对，本来就没关系我为什么要撇清关系，但喜闻乐见的话肯定不在其中。毕竟此事一出我还觉得自己亏了不少呢。

last of the last

    看到这篇文章发布之后下面的相关推荐，看懂过之后其实应该知道，其实等额本息和等额本金无所谓谁更划算，其真相是"一旦利率和复利计算周期定了，那么便没有本质差别了"。大家要做的只是根据自己的能力选择适合自己的还款方式。

   当然，目前的资金方一般只给出了这两种还款方式，可谓能选择的余地并不多，在以上代码的基础上其实可以继续推广，实现周期内还款任意金额的后续计算，那么用户每一期就可在一定范围内想还多少还多少，也不存在“现在什么提前还款还要申请”之类的。当然这种定制化不怎么存在的原因并太不是技术原因，而是预算管理，除了方便计算之外，资金方需要对资金进行预期，并依据此管理一些资金策略。