浅谈数据结构与算法(三)
数据结构与算法(三)
- 栈
- 顺序栈
- 链栈
- 队列
- 顺序队列
- 链式队列
- 双端队列
栈
- 栈的定义
栈(stack) 又称堆栈,它是运算受限的线性表。
其限制就是只允许在表的一端进行插入和删除,不允许在其他位置进行删除、查找、添加等操作。
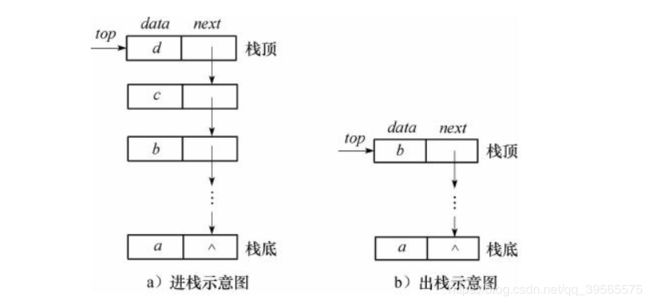
表中进行插入、删除操作的一端叫做栈顶(top),栈顶保存的元素为栈顶元素。相对的表的另一端为栈底。
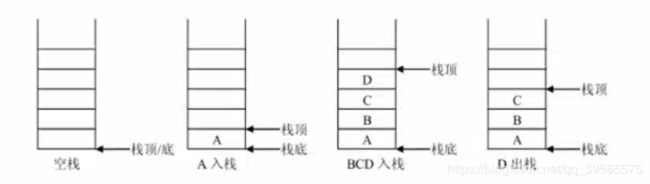
- 栈中没有元素时称为空栈
- 向栈中添加元素称为入栈或进栈。
从栈中删除元素称为出栈或退栈 - 由于栈的插入仅在栈顶操作,所以后插入的元素肯定先出栈,所以又把堆栈称为后进先出栈(Last in first out,简称LIFO)
上代码:
/*
* 定义栈接口
* 定义栈主要操作
*/
public interface Stack {
// 返回堆栈的大小
public int getSize();
// 判断堆栈是否为空
public boolean isEmpty();
// 数据元素 e 入栈
public void push(Object e);
// 栈顶元素出栈
public Object pop();
// 取栈顶元素
public Object peek();
}
这里要留意一下,栈操作的专业词汇:pop、push、peek
- 栈的存储结构
和线性表相似,栈也对应两种存储结构,顺序存储结构和链式存储结构
顺序栈
是使用顺序存储结构的堆栈,即利用一组地址连续的存储单元依次存储堆栈中的数据元素
由于堆栈是一种特殊的线性表,即在线性表顺序存储结构的基础上,选择线性表的一端作为栈的栈顶。
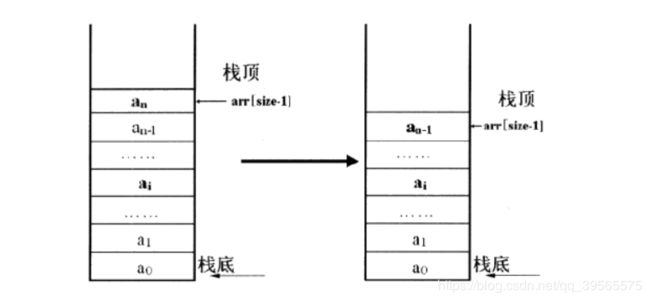
根据数组操作的特性,选择数组下标最大的一端,即线性表顺序存储的表尾作为栈顶,此时入栈和出栈都可以在O(1)完成。
由于堆栈的操作都在栈顶完成,因此在顺序栈的实现中需要附设一个指针top来动态的指示栈顶元素在数组中的位置,通常top可以用栈顶元素在数组中的下标来表示,当top = -1时,此时为空栈
上代码:
/*
* 基于数组实现的顺序栈
*/
public class ArrayStack<E> {
private Object[] data = null;
//栈容量
private int maxSize = 0;
//栈顶指针
private int top = -1;
//初始化栈容量
ArrayStack() {
this(10);
}
ArrayStack(int initialSize){
if (initialSize >= 0) {
this.maxSize = initialSize;
data = new Object[initialSize];
top = -1;
}else {
throw new RuntimeException("初始化容量不能小于0" + initialSize);
}
}
//判断是否为空栈
public boolean isEmpty(){
return top == -1 ? true : false;
}
//进栈,第一个元素top=0
public E push(E e) {
if (top == maxSize -1) {
throw new RuntimeException("栈已满,无法添加元素");
}else {
data[++top] = e;
return e;
}
}
//取出栈顶元素但不删除
public E peek() {
if (top == -1) {
throw new RuntimeException("栈为空");
}else {
return (E)data[top];
}
}
//弹出栈顶元素
public E pop() {
if (top == -1) {
throw new RuntimeException("栈为空");
}else {
return (E)data[top--];
}
}
//返回对象在堆栈中的位置,以1为基数
public int search(E e) {
int i = top;
while(top != -1) {
if (peek() != e) {
top --;
}else {
break;
}
}
int result = top + 1;
top = i;
return result;
}
}
看这段代码的时候,你要记得它是个栈。。。。。。。
链栈
链栈采用链表作为存储结构结构实现的栈
当采用单链表存储线性表时,根据单链表的操作特性选择单链表的头部作为栈顶,此时出栈、入栈都可以在O(1)完成。
由于堆栈的操作只在线性表的一端进行,在这里使用带头结点的单链表或不带头结点的单链表都可以。
使用带头结点的单链表时,结点的插入和删除都在头结点之后进行;
使用不带头结点的单链表时,结点的插入和删除都在链表的首结点上进行。
public class LinkedStack<E> {
public class Node<E>{
E e;
Node<E> next;
public Node(){
}
public Node(E e, Node next){
this.e = e;
this.next = next;
}
}
//栈顶元素
private Node<E> top;
//当前栈的大小
private int size;
public LinkedStack() {
top = null;
}
//当前栈大小
public int length() {
return size;
}
public boolean empty() {
return size == 0;
}
//入栈,让top指向新的元素,新元素的next指向原来的栈顶元素
public boolean push(E e) {
top = new Node(e, top);
size++;
return true;
}
//查看栈顶元素但不删除
public Node<E> peek(){
if (empty()) {
throw new RuntimeException("栈为空");
}else {
return top;
}
}
//出栈
public Node<E> pop(){
if (empty()) {
throw new RuntimeException("栈为空");
}else {
Node<E> value = top;
top = top.next;
value.next = null;
size --;
return value;
}
}
}
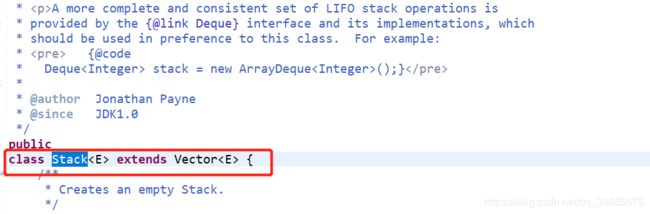
看源码的时候Stack是继承自Vector的,而Vector已经过时了,所以相对来说Stack也过时了,只是Stack这个类过时了,但是栈这种数据结构还是有引用的,接下来往下看。。。。
接下来到了队列了。。。- _ -#
队列
-
队列的定义
队列(queue )简称队,它同堆栈一样,也是一种运算受限的线性表,
其限制是仅允许在表的一端进行插入,而在表的另一端进行删除。
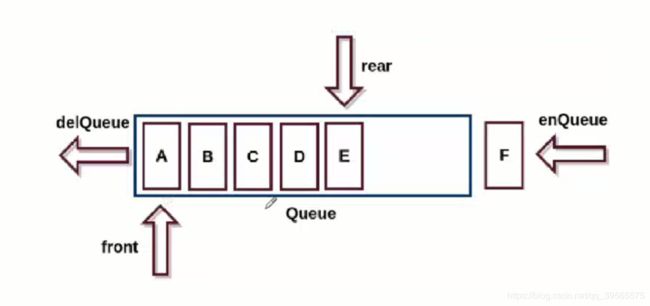
在队列中把插入数据元素的一端称为 队尾(rear) ),删除数据元素的一端称为 队首(front) )。 -
向队尾插入元素称为 进队或入队,新元素入队后成为新的队尾元素;
从队列中删除元素称为 离队或出队,元素出队后,其后续元素成为新的队首元素。 -
由于队列的插入和删除操作分别在队尾和队首进行,每个元素必然按照进入的次序离队。
也就是说先进队的元素必然先离队,所以称队列为 先进先出表(First In First Out,简称FIFO)。
public interface Queue {
// 返回队列的大小
public int getSize();
// 判断队列是否为空
public boolean isEmpty();
// 数据元素 e 入队
public void enqueue(Object e);
// 队首元素出队
public Object dequeue();
// 取队首元素
public Object peek();
}
顺序队列
方法一:使用数组作为存储结构
public class Queue<E> {
private Object[] data = null;
//队列容量
private int maxSize;
//队列头,允许删除
private int front;
//队列尾,允许插入
private int rear;
//构造函数
public Queue(){
this(10);
}
public Queue(int initialSize){
if(initialSize >=0){
this.maxSize = initialSize;
data = new Object[initialSize];
front = rear =0;
}else{
throw new RuntimeException("初始化大小不能小于0:" + initialSize);
}
}
//判空
public boolean empty() {
return front == rear ? true : false;
}
//入队
public boolean add(E e) {
if (rear == maxSize) {
throw new RuntimeException("队列已满");
}else {
data[rear++] = e;
return true;
}
}
//获取队首元素,但不删除
public E peek() {
if(empty()) {
throw new RuntimeException("队列为空");
}else {
return (E)data[front];
}
}
//出队
public E poll() {
if (empty()) {
throw new RuntimeException("队列为空");
}else {
E value = (E)data[front];//保留队列的front端的元素的值
data[front++] = null;//释放队列的front端的元素
return value;
}
}
//队列长度
public int length() {
return rear - front;
}
}
缺点: 如果顺序队列使用数组作为存储结构,当每次进行出队操作将数据弹出去后(即如果A出队以后,front指针就会移到B,但是之前A的存储空间存在,如果队列不是一直保持满队列的情况下,那么该空间就会一直处于闲置的状态从而导致空间上的浪费),就再也不会使用front之前的空间了,这些空间就会将一直处于闲置状态,导致空间的浪费。
方法二:使用循环数组作为存储结构
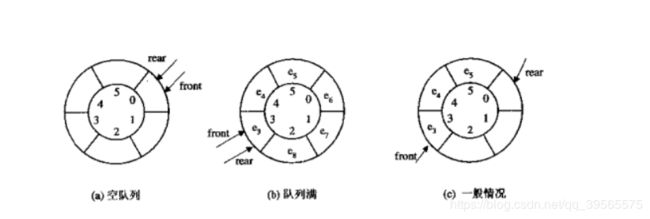
为了解决上述问题,将普通数组换成循环数组。在循环数组中,末尾元素的下一个元素不是数组外,而是数组的头元素。
这样就能够再次使用front之前的存储空间了
- a种情况: 当队列为空的时候,front和rear指针都指向队列的起始位置
- b中情况: 当队列为满的时候,front和rear指针都指向队列的第一个元素,这样front指针既是指向头又是指向尾。
- c种情况: 当队列为一般情况的时候,front还是会指向位于队列第一个元素,rear则指向队列最后一个元素的下一个位置。
上代码。。。。。
public class LoopQueue<E> {
public Object[] data = null;
//队列容量
private int maxSize;
//队列头,只允许删除
private int front;
//队列胃,只允许插入
private int rear;
//队列当前长度
private int size =0;
public LoopQueue() {
this(10);
}
public LoopQueue(int initialSize) {
if (initialSize >= 0) {
this.maxSize = initialSize;
data = new Object[initialSize];
front = rear = 0;
} else {
throw new RuntimeException("初始化大小不能小于0:" + initialSize);
}
}
// 判空
public boolean empty() {
return size == 0;
}
public boolean add(E e) {
if (size == maxSize) {
throw new RuntimeException("队列已满,无法插入新的元素!");
}else {
data[rear] = e;
rear = (rear + 1) % maxSize;
size ++;
return true;
}
}
// 返回队首元素,但不删除
public E peek() {
if (empty()) {
throw new RuntimeException("空队列异常!");
} else {
return (E) data[front];
}
}
// 出队
public E poll() {
if (empty()) {
throw new RuntimeException("空队列异常!");
} else {
E value = (E) data[front]; // 保留队列的front端的元素的值
data[front] = null; // 释放队列的front端的元素
front = (front+1)%maxSize; //队首指针加1
size--;
return value;
}
}
// 队列长度
public int length() {
return size;
}
//清空循环队列
public void clear(){
Arrays.fill(data, null);
size = 0;
front = 0;
rear = 0;
}
}
链式队列
- 队列的链式存储可以使用单链表来实现。为了操作实现方便,这里采用带头结点的单链表结构。
- 根据单链表的特点,选择链表的头部作为队首,链表的尾部作为队尾。
- 除了链表头结点需要通过一个引用来指向之外,还需要一个对链表尾结点的引用,以方便队列的入队操作的实现。
为此一共设置两个指针,一个队首指针和一个队尾指针,如图 所示。
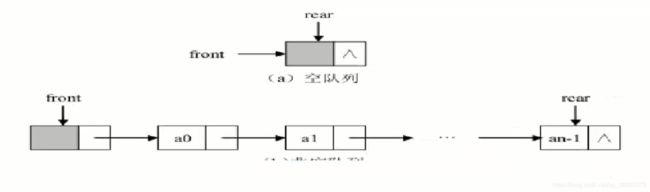
队首指针指向队首元素的前一个结点,即始终指向链表空的头结点,队尾指针指向队列当前队尾元素所在的结点。 当队列为空时,队首指针与队尾指针均指向空的头结点,标红的部分基本就是它的设计思想,有了设计思想代码就可以写出来了
public class LinkQueue<E> {
public class Node<E>{
E e;
Node<E> next;
public Node(){}
public Node(E e, Node next){
this.e = e;
this.next = next;
}
public E getE() {
return e;
}
public void setE(E e) {
this.e = e;
}
public Node<E> getNext() {
return next;
}
public void setNext(Node<E> next) {
this.next = next;
}
}
private Node front;//队列头
private Node rear;//队列胃
private int size;//队列当前长度
public LinkQueue() {
front = null;
rear = null;
}
public boolean empty() {
return size == 0;
}
public boolean add(E e) {
if (empty()) {
//如果只有一个节点,front和rear都指向一个节点
front = new Node(e, null);
rear = front;
}else {
Node<E> newNode = new Node<E>(e,null);
rear.next = newNode; //让尾指针的next指向新的元素
rear = newNode;//把新节点作为新的尾结点
}
size++;
return true;
}
public Node<E> peek(){
if (empty()) {
throw new RuntimeException("队列为空");
}else {
return front;
}
}
public Node<E> pop(){
if (empty()) {
throw new RuntimeException("队列为空");
}else {
Node<E> value = front; //得到队列头元素
front = front.next; //将头元素的next指向下一个元素
value.next = null;//将原来的头元素next引用释放掉
size--;
return value;
}
}
public int length() {
return size;
}
}
好记性不如烂笔头,敲一敲吧~~~~
双端队列
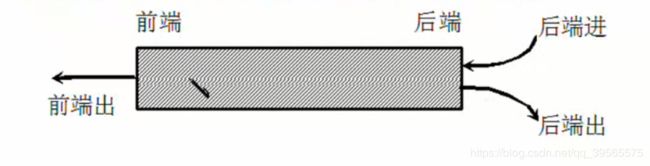
所谓双端队列是指两端都可以进行进队和出队操作的队列,如下图所示,将队列的两端分别称为前端和后端,两端都可以入队和出队。其元素的逻辑结构仍是线性结构。
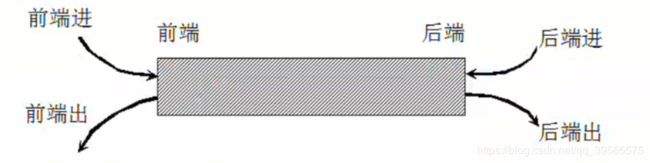
- 在双端队列进队时,前端进的元素排列在队列中后端进的元素的前面,后端进的元素排列在队列中前端进的元素的后面。
- 在双端队列出队时,无论前端出还是后端出,先出的元素排列在后出的元素的前面。
输出受限的双端队列:
即一个端点允许插入和删除,另一个端点只允许插入的双端队列。

输入受限的双端队列:
即一个端点允许插入和删除,另一个端点只允许删除的双端队列。
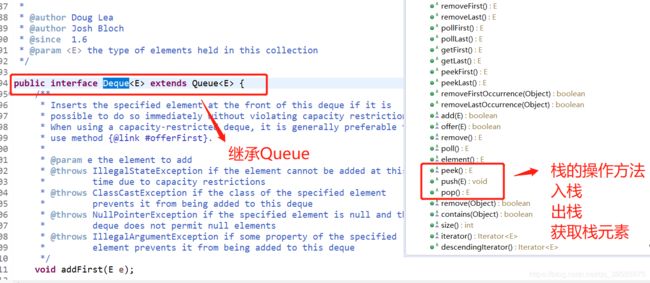
这里就要想一下,如果只在一端进行输入和输出,那么它是不是就变成栈了。所以双端队列既可以当栈使用,也可以当队列来使用。之前提到过Stack和Vector已经过时了,然而其实Stack的实现就在队列里,如下图所示:
锊一下栈、队列、链表的关系,如下图所示:
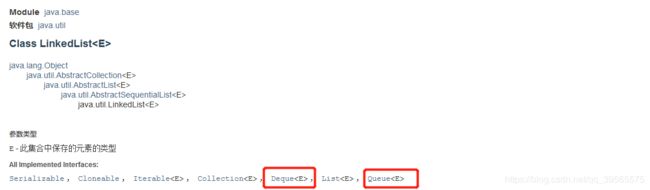
我们可以看到链表实现的接口有Deque和Queue,Deque里面又有栈的操作方法,所以可以看出栈和队列的底层其实就是链表,我们再来看一下Queue,如下图所示:
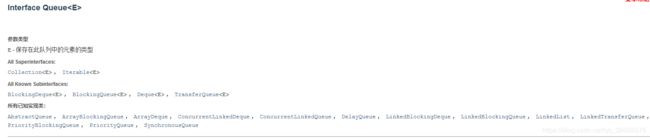
Queue扩展了java.util.Collection接口。怎么扩展的。。。。接着如下图所示:

通过看API可以看出,具体是咋拓展的,总结一下:
- Queue使用时要尽量避免Collection的add()和remove()方法,而是要使用offer()来加入元素,使用poll()来获取并移出元素。它们的优点是通过返回值可以判断成功与否,add()和remove()方法在失败的时候会抛出异常。 如果要使用前端而不移出该元素,使用element()或者peek()方法。
队列这一块没有上代码,因为我自己也是有选择性的实现了几个,网上有很多更好的demo,最好试着去看一下源码,体会一下设计者的巧妙思想,至少现在乃至未来一段时间都写不出那样的代码。。。。。咳咳,浅谈浅谈,重要的是理解它的设计思路。
接下来就是树、图、哈希。。。。。想把它单独拿出来,这些东西现在是用的最多的,我也真的很想把它们锊顺了,搞懂了。
本博客文章皆出于学习目的,个人总结或摘抄整理自网络。引用参考部分在文章中都有原文链接,如疏忽未给出请联系本人。另外,如文章内容有错误,欢迎各方大神指导交流。