数据挖掘技术 知识点整理

ch01 绪论

课内重点

Q1. 数据仓库的四个特征

• 面向主题
• 集成的
• 不可修改
• 随时间变化

Q2. 数据仓库数据的粒度与组织

• 数据的粒度是指数据仓库的数据单元中所保存数据的综合程度
• 数据的综合程度越高，其粒度越粗
• 数据仓库存储的数据粒度越细，则占用的存储空间越大，但提供的更细节的查询

Q3. 知识发现概念

• 定义：知识发现（KDD）就是采用有效算法从大量的、不完全的、有噪声的、模糊和随机的数据中识别出有效的、新颖的、潜在有用乃至最终可理解的模式（Pattern）的非平凡过程
• 过程：
  • 数据采集
  • 数据预处理
  • 数据挖掘
  • 知识评价
  • 知识应用
• 知识发现过程中一个特定而关键的步骤：数据挖掘

Q4. 数据挖掘的数据来源

• 数据库
  • 传统数据库（DB）
  • 数据仓库（DW）
  • 空间数据库（Spatial Database）
  • 时态数据库和时间序列数据库（Temporal Database and Time-Series Database）
  • 多媒体数据库（Multimedia Database）
  • 文本数据库（Text Database）
• 非数据库
  • 数据流（Data Stream）
  • Web数据

Q5. 数据挖掘的步骤

• 问题定义
• 数据准备
  • 数据抽取
  • 数据预处理
  • 数据存储
• 挖掘实施
• 评估解释
• 知识应用
  

Q6. 数据仓库与数据挖掘的区别

• 结论：数据仓库不是为数据挖掘而生的，反过来数据挖掘也不是为数据仓库而活。它们是支持决策的两个相对独立的知识体系

Q7. 数据仓库与数据挖掘的联系

一个中心（决策支持），两个基本点（DW，DM）

• DW为DM提供了更好的、更广泛的数据源
• DW为DM提供了新的数据支持平台
• DW为DM提供了方便
• DM为DW提供了更好的决策支持工具
• DM为DW的数据组织提出了更高的要求
• DM为DW提供了广泛的技术支持

---

课后练习题

4. 简述数据仓库的定义

答： 数据仓库是一个面向主题的、集成的、不可修改的、随时间变化的，支持管理决策的数据集合

5. 简述数据库与数据仓库的关系

答：数据仓库，是在数据库已经大量存在的情况下，为了进一步挖掘数据资源、为了决策需要而产生的，数据仓库的出现，并不是要取代数据库。目前，大部分数据仓库还是用关系数据库管理系统来管理的。可以说，数据库、数据仓库相辅相成的

相关：
数据库与数据仓库的区别：

• 数据库是面向事务设计的，数据仓库是面向主题设计的
• 数据库一般存储在线交易数据，数据仓库存储的一般是历史数据
• 数据库是为捕获数据而设计，数据仓库是为分析数据而设计
• 事务系统是实时的，而分析系统是事后的

6. 简述数据仓库特征

答：

• 面向主题
• 集成的
• 不可修改
• 随时间变化

11. 简述数据挖掘的主要步骤

答：

• 问题定义
• 数据准备
• 挖掘实施
• 评估解释
• 知识应用

ch02 数据仓库原理

课内重点

Q1. 多数据源的问题

• 数据不一致：数据之间的矛盾性和不相容性。如职务升迁了，但工资数据却没有改变
• 属性差异：性别属性有的取“男”/“女”,长度为2；有的取“1”/“0”，长度为1
• 数据重复：数据源中存在两条或多条完全相同的记录，或者同一个数据冗余地存在于多个数据源中
• 数据不完整：某些属性的值可能是缺失的，甚至是错误的数据
• 数据噪声：测量数据时遇到的随机或其它不确定因素，导致被测量的数据产生了偏差或错误
• 高维数据：为较全面的描述实体，原始数据通常都使用了较多属性
• 模式不统一：将集成为单一数据集的多个数据源的模式不同。如“常住人口数据”和“暂住人口数据”两张表，前者有128个属性，后者也有98个属性
• 数据不平衡：数据集中某一类样本的数量明显少于其他类型样本的数量

Q2. 数据预处理

• 定义：在多数据源集成为统一数据集之前进行的数据清洗、数据变换、数据规约等数据处理过程
• 目的：清除多数据源集成存在的问题，为数据仓库或数据挖掘提供一个完整、干净、准确、且有针对性的数据集合

Q3. 数据清洗

定义：发现并纠正数据源，即原始数据中存在的问题或错误的过程，包括检查数据一致性，处理无效值、填补缺失值、以及过滤掉那些不符合要求的数据等

• 属性的处理：
  • 重命名属性
  • 统一属性
  • 处理主键属性
  • 派生新属性
  • 选择相关属性
• 空值的处理：
  • 人工填补
  • 忽略记录
  • 忽略属性
  • 使用默认值
  • 使用平均值
  • 使用预测值
• 数据噪声处理
  • 等深分箱法
  • 等宽分箱法
  • 用户自定义区间
    • 按平均值平滑
    • 按边界值平滑
    • 按中值平滑
• 不平衡数据处理
  • 过抽样
  • 欠抽样

Q4. 等深分箱法

计算思路：
把数据集中的数据按照排列顺序分配到k个箱子中(k=1,2,…,k)

• 当k 整除 n时，令p=n/k，则每个箱子都有p个数据，即
  第1个箱子的数据为：a₁，a₂，…，a_p；
  第2个箱子的数据为：a_p+1，a_p+2，…，a_2p；
  ……
  第k个箱子的数据为：a_n-p+1，a_n-p+2，…，a_n；
• 当k 不能整除 n时，令p=n/k [向下取整]，q=n-k*p，则可让前面q个箱子有p+1个数据，后面k-q个箱子有p个数据，即
  第1个箱子的数据为：a₁，a₂，…，a_p+1；
  第2个箱子的数据为：a_p+2，a_p+3，…，a_2p+2；；
  ……
  第k个箱子的数据为：a_n-p+1，a_n-p+2，…，a_n
  也可让前面k-q个箱放p个数，后面q个箱放p+1个数据

例题：
设A={1, 2, 3, 3, 4, 4, 5, 6, 6, 7, 7, 8, 9,11}共14个数据，请用等深分箱法将其分成k=4个箱子

Q5. 等宽分箱法

计算思路：
把数据集最小值和最大值形成的区间分为k个左闭右开的子区间（最后一个除外）I₁，I₂，…，I_k。如果a_i 属于 I_j就把数据a_i放入第j个箱子

例题：
设A={1, 2, 3, 3, 4, 4, 5, 6, 6, 7, 7, 8, 9,11}共14个数据，请用等深分箱法将其分成k=4个箱子

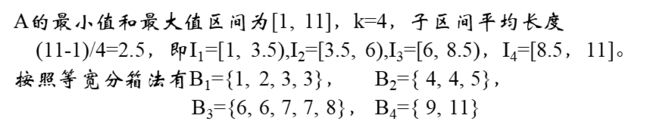
Q6. 数据变换

• 数据聚集：对数据按照管理或挖掘需要进行汇总
• 数据概化：用较高层次的数据代替较低维度层次的数据
• 数据规范化：将原始数据按照一定的比例缩放，使之落入一个特定的区间
  • 最小—最大规范化
    
  • 零—均值规范化
    
  • 小数定标规范化
    

Q7. 数据规约

定义：用精简数据表示原始数据的方法，且归约后数据量通常比原始数据小很多，但具有接近甚至等价于原始数据表达的信息

• 维归约：减少描述问题的随机变量个数
• 属性归约：减少描述问题的数据集的属性个数
• 数量归约：用较少的数据表示形式替换原始数据
• 数据压缩：使用变换方法得到原数据的归约或“压缩”表示，图像压缩技术就是一种典型的数据压缩方法

Q8. 数据仓库的概念模型

• 定义：对现实管理决策中各个主题及其特征的数据抽象表示
• 特点：
  • 能够比较真实地模拟或抽象表示用户的决策主题
  • 表示方法简单直观且易于用户理解
  • 与计算机系统支持的具体数据模型无关
  • 易于向数据仓库的逻辑数据模型转换

Q9. 星型模型

• 特点
  • 星型模型由一个事实表和多个维度表的连接表示多维数据模型，矩形：事实表，凹圆角矩形表示维度表，并用直线表示其间的主键-外键联系
    
  • 星型模型是多维数据模型在关系数据库中的组织和存储结构描述，即它是多维数据模型的关系模型表示方法。因此，星型模型是多维数据模型的一种逻辑模型
• 优势
  • 星型模型围绕一个确定的主题，体现了数据仓库对数据结构和组织的要求
  • 星型模型表达直观，易于理解且设计相对容易
  • 星型模型维度表包含了用户经常查询和分析的属性，优化了对数据库的浏览，在维度表和事实表之间没有任何“迷宫”，使查询的过程变得简单而直接
  • 星型模型为OLAP提供了良好的工作条件，使OLAP能通过星形连接和星形索引，显著提高查询性能
  • 设计相对较为简单
• 不足
  • 维度表通常是非规范化的，造成很大的数据冗余
  • 由于星型模型中各个维度表主键的组合构成事实表的主键，导致维度的变化非常复杂、费时
  • 维度属性的复杂形成的大维度问题
  • 处理维的层次关系比较困难
  • 无法表达“多对多”的联系

Q10. 雪花模型

概念

• 雪花模型是星形模型按照关系数据库规范化理论对维度表进行分解的结果
• 目的：消除数据冗余，同时增加更多对事实进行细节描述的信息，提高查询分析的灵活性
• 其查询效率通常比星型模型表示的多维数据集要低一些

优势：

• 减少了一定数据冗余量，节约了许多存储空间
• 处理复杂维度和更新维度更加容易
• 表示“多对多”的联系方便
• 查询分析更具灵活性

不足：

• 事实表与维度表、详细类别表联系比较复杂，用户不易理解
• 浏览查询多维数据内容相对困难
• 额外的详细类别连接操作导致查询性能下降

Q11. 位图索引模型

• 重要实用：在数据仓库的存储结构中，位图索引是一项非常重要且实用的索引模型
• 索引条件：对于那种只取少量几个离散值的属性列（属性取值种类在1%以下）来说，位图索引就是用一个二进制串，替代基本表中某一列的取值
• 索引效果：使我们在不触及数据记录的情况下，直接通过位图索引快速地获得查询结果

---

课后练习题

5.试述对一个数据集采用分箱技术包含的主要步骤

• 对数据集的数据进行排序
• 确定箱子个数k、选定数据分箱的方法并对数据集中数据进行分箱
• 选定处理箱子数据的方法，并对其重新赋值
  • 常用分箱方法：等深分箱、等宽分箱、自定义区间、最小熵分箱法

6. 设数据集A={1,1,3,3,4,5,5,5,6,7,7,7,9,10,12,15}，请用等深分箱法将其分成k=4个箱子

7. 设数据集A={1,1,3,3,4,5,5,5,6,7,7,7,9,10,12,15}，请用等宽分箱法将其分成k=4个箱子

16. 数据仓库有哪几种逻辑模型？

• 多维模型
• 星型模型
• 雪花模型

ch03 数据仓库的设计开发应用

课内重点

Q1. 数据仓库设计的特点及含义

“数据驱动”的设计

• 数据仓库是从已有数据出发的设计方法，即从数据源抽取数据，经转换形成面向主题，支持决策的数据集合
• 以全面了解并利用现有数据为出发点

“分析驱动”的设计

• 是从决策分析需求出发的设计
• 从已有数据源出发，按照决策分析主题对数据源中数据及其之前的联系重新考察，并重新组织形成数据仓库分析需要的主题数据

“需求模糊”的设计

• 数据仓库设计的数据分析处理需求更加灵活，也没有固定的模式，有时用户自己对所要进行的分析处理也不能事先确定
• 数据仓库的分析需求在设计初期往往是模糊或不明确的，通常只有在数据仓库设计过程中，或后来数据仓库的决策支持过程中逐渐明确

“螺旋周期”的设计

• 数据仓库系统的开发是一个动态反馈启发式的循环过程，也称为螺旋上升的周期性开发过程，即“螺旋周期”
• 数据仓库的数据内容、结构、粒度、分割以及其他物理设计，需要根据用户使用数据仓库所反馈的意见和建议进行调整，以提高系统的效率和性能
• 用户在使用数据仓库进行决策过程中，不断提出新的决策分析需求，增加新的主题，使数据仓库进入新一轮的设计周期，数据仓库进一步完善，为用户提供更准确、更有效的决策信息

Q2. 数据仓库系统开发过程

5个时期划分方式

• 规划时期
• 设计时期（需求分析、概念分析、逻辑设计、物理设计）
• 实施时期
• 开发时期
• 应用时期

3个阶段划分方式

• 规划设计阶段（规划时期、设计时期）
• 实施开发阶段（实施时期、开发时期）
• 使用维护阶段（应用时期）

Q3. 了解虚拟数据仓库与数据集市

• 虚拟数据仓库：决策支持功能直接在事务处理数据库上实现
• 单纯数据仓库：从数据源中抽取、转换和加载到一个统一的数据仓库之中，各部门的查询和分析功能都从这个统一的数据仓库中进行
• 单纯数据集市：一个部门使用的数据仓库，因为企业中的每个职能部门都有自己的特殊管理决策需要，而统一的数据仓库可能无法同时满足这些部门的特殊要求
• 完整数据仓库：数据仓库从企业各种数据源抽取数据，部门数据集市从企业数据仓库中获取数据

Q4. ETL

数据抽取、转换和装载（Extraction-Loading-Transformation，ETL）

---

课后练习题

4. 数据仓库系统开发需要经历哪几个时期？

若划分为5个时期

• 规划时期：项目规划
• 设计时期：需求分析、概念设计、逻辑设计、物理设计
• 实施时期：DW创建，ETL
• 开发时期：应用开发
• 应用时期：决策支持、维护评价

若划分为3个时期

• 规划设计阶段（规划时期、设计时期）
• 实施开发阶段（实施时期、开发时期）
• 使用维护阶段（应用时期）

5. 简述数据仓库设计时期的主要工作内容

• 决策需求调查、数据仓库环境分析，数据仓库开发需求确定
• 各种模型的建立，包括多维数据模型、星型模型、雪花模型和物理模型等，特别是数据源的属性列与数据仓库目标列的映射关系等，并根据选择的数据仓库管理系统，完成相应的物理设计

ch04 警务数据仓库的实现

课内重点

Q1. SSIS包后缀是什么

.dtsx

ch05 联机分析处理（OLAP）技术

课内重点

Q1. OLAP的12条准则

• 多维概念的视图（multidimensional conceptual view）
  从用户的角度来看，整个企业的数据视图本质是多维的（时间，地点，品种），因此OLAP的概念模型也应该是多维的
• 透明性（transparency）
  • 用户不必关心表格或图显的数据的来源，只用OLAP工具查询数据
  • OLAP系统应该是开放系统架构的一个部分，当按用户需要将OLAP系统嵌入到架构的任何地方都不影响 OLAP分析工具的性能
• 存取能力 （accessibility）
  • OLAP系统应该有能力利用自有的逻辑结构访问异构数据源，并且进行必要的转换以提供给用户一个连贯的展示
  • 还能提供高效的存取策略
• 稳定的报表性能（consistent reporting performance）
  当数据的维度和数据综合层次增加时，OLAP系统为最终用户提供报表的能力和相应速度不应该有明显的降低和减慢
• 客户/服务器体系结构（client/server architecture）
  OLAP系统应该是一种客户/服务器（C/S）应用结构，并有足够的智能保证多维数据服务器能被不同的客户应用工具以最小的代价访问
• 维的等同性（generic dimensionality）
  每个数据维度应该具有等同的层次结构和操作能力，比如对每个维度都可以进行“切片”、“切块”和“旋转”等相同的操作
• 动态的稀疏矩阵处理能力（dynamic sparse matrix handling）
  • 多维数据集的稀疏特性，即大多数单元格的值都是零
  • 若存储所有这些零值数据就会占用大量的存储空间
  • OLAP系统应该为这种具有稀疏性的多维数据集的存储和查询分析提供一种“最优”处理能力，既尽量减少零值单元格的存储空间，又保证动态查询分析的快速、高效
• 多用户支持能力（multi-user support）
  OLAP应提供并发获取和更新访问，保证完整性和安全性的能力
• 非受限的跨维操作（unrestricted cross-dimensional operations）
  多维数据之间存在固有的层次关系，这就要求OLAP工具能自己推导出而不是最终用户明确定义出相关的计算
• 直观的数据操作（intuitive data manipulation）
  OLAP工具应为数据的分析操纵提供直观易懂操作界面，比如“下钻”、“上卷”、“切片”等多维数据分析方法都可以通过直观、方便的点击操作完成
• 灵活的报表生成（flexible reporting）
  OLAP提供的报表功能应该以用户需要的任何方式展现信息，以充分反映数据分析模型的多维特征
• 非受限维与聚集层次（unlimited dimensions and aggregation levels）
  • OLAP工具不应该为多维数据的维度数量和维度层次数量设置任何限制
  • 说明：这个要求对系统要求有点高，可以适当降低要求。因为在实际应用中，多维数据集的维度数量很少超过15个，维度层次也通常在6个以内

说明
联机分析处理（On-Line Analysis Processing，OLAP）：针对特定问题的联机多维数据快速访问和分析处理的软件技术、能帮助决策者对数据进行深入的多角度观察

Q2. OLAP的简要准则

联机分析处理（OLAP）就是共享多维信息的快速分析，即FASMI（Fast Analysis of Shared Multidimensional Information）

• 快速性（Fast）
  • 用户对OLAP系统的快速反应能力有很高的要求，希望系统能在5秒内对用户的大部分分析要求做出反应
  • 快速性需求必须在线响应才能完成，故又称为在线性
  • 快速性还需要一些专门的技术支持，如专门的数据存储结构、大量数据的预先计算、还有硬件特别设计等
• 分析性（Analysis）
  • OLAP系统应能处理与应用有关的任何逻辑分析和统计分析
  • 例如，连续时间序列分析、成本分析、意外报警等
  • 此外，还应使用户无须编程就可以定义新的计算，并作为查询分析的一部分，以用户理想的方式给出报告
• 共享性（Shared）
  • OLAP系统必须提供并发访问控制机制，让多个用户共享同一OLAP数据集的查询分析，并保证数据完整性和安全性
• 多维性（Multidimensional）
  • OLAP系统必须提供对数据分析的多维视图，包括对层次维和多重层次维的完全支持
  • 事实上，多维分析是分析企业数据最有效的方法，是OLAP系统的灵魂和关键特性
• 信息性（Information）
  • 无论数据量有多大，也不管数据存储在何处，OLAP系统应能及时获得信息，并且能管理大容器信息

关键特征：快速性和多维性

Q3. OLAP的多维分析操作

• 切片（slice）
• 切块（dice）
• 下钻（drill-down）
• 上卷（roll-up）
• 旋转（pivot）

Q4. 切片

• 在n(>=3)维数据集的某一维上，指定一个维成员的选择操作
• 若对一个n维数据集进行切片操作，则将得到一个n-1维的数据集
• 多维数据集的维度越高，人们对其理解就越困难
• 切片操作是对多维数据集进行降维处理，方便用户理解多维数据蕴藏的决策信息
• 从n(>=2)维数据集中选择一个2维子集的操作称为局部切片操作
• 对任意n(>=2)维数据集，其局部切片操作结果永远是2维数据集

Q5. 切块

• 在n(>=3)维数据集的某一维上指定若干维成员的选择操作
• 对于n(>=3)维数据集，如果某一维上指定的维度成员数大于等于2，则切块操作的结果仍然是一个n维数据集（仅当指定一个维度成员时，其切块操作的结果是一个切片）

Q6. 旋转

• 在多维数据集展示的时候，对其改变维的显示方向的操作
• 多维数据集的旋转结果仍然是原先的多维数据集，它仅仅改变了数据集展示的方位，方便用户观察数据

Q7. 钻取

• 多维数据集的钻取就是改变数据所属的维度层次，变换数据分析的粒度，它是下钻和上卷这两个相反操作的统称
• 目的：方便用户从不同维度的不同层次观察多维数据

---

上卷

• 对多维数据选定的维度成员，按照其上层次维度对数据进行求和计算并展示的操作
• 它是在某一维度上，将低层次的细节数据概括为高层次的汇总数据，以增大数据的粒度，并减少了数据单元格个数或数据的维度

下钻

• 对多维数据选定的维度成员，按照其下层次维度对数据进行分解的操作
• 它从由当前的汇总数据深入到其下一层次的细节数据，以便用户观察到更为细粒度的数据

Q8. OLAP、DW与DM的联系

• OLAP（联机分析处理）、DW（数据仓库）与DM（数据挖掘）是相互独立而又相互联系的3个概念
• 相互独立：它们在不同的时间，由不同的学者或组织分别提出，因此它们在基本内涵，解决的主要问题和使用的基本技术上都有很大的区别
• 相互联系：它们都是为了支持企业的管理决策这一中心任务，即共同目标而提出的。因此，我们可以用“一个中心，三个基本点”来形容DW、OLAP、DM之间关系
  

Q9. OLAP、DW与DM的区别

课后练习题

4. 写出FASMI的英文短语，并简述其含义

• fast：快速性，指用户对OLAP系统的快速反应能力要求很高
• analysis：分析性，指OLAP系统应能处理与应用有关的任何逻辑分析和统计分析
• shared：共享性，指OLAP系统必须提供并发访问控制机制，让多个用户共享同一OLAP数据集的查询分析，并保证数据完整性和安全性
• multidimensional：多维性，指OLAP系统必须提供对数据分析的多维视图
• information：信息性，指OLAP系统应能及时获得信息，并且能管理大容量信息

5. 在OLAP的5个特征FASMI中，哪两个是OLAP的关键特性？

• 快速性
• 多维性

6. 多维数据分析有哪几种基本分析操作？

• 切片
• 切块
• 下钻
• 上卷
• 旋转

7. 简述多维数据集“切片”（slice）操作的含义，并举例说明切片操作的结果

• 含义：在数据集的某一维上，指定一个维成员的选择操作
• 举例：若对一个3维数据集进行切片，会得到一个2维的数据集

8. 简述多维数据集“下钻”（drill down）操作的含义，并举例说明下钻操作的结果

• 含义：对多维数据选定的维度成员，按照其下层次维度对数据进行分解的操作
• 举例：“1季度”这个数据集，将其下钻到下层次“月”，则得到“1月”、“2月”、“3月”

9. 简述多维数据集“上卷”（roll up）操作的含义，并举例说明上卷操作的结果

• 含义：对多维数据选定的维成员，按照其上层次维度对数据进行求和计算并展示的操作
• 举例：将时间维“1月”、“2月”、“3月”上卷恰好为“季度”的层次，即“1季度”

10. 简述多维数据集“切块”（dice）操作的含义，并举例说明切块操作的结果

• 含义：在数据集的某一维上指定若干维成员的选择操作
• 举例：对于一个3维数据集进行切片，还是得到3维的数据集

ch07 数据的属性与相似性

课内重点

Q1. 数据集的结构

• 二维表
  
• 数据矩阵
  

Q2. 属性的类型

• 连续属性：通常在一个实数区间内取值，因此其取值个数理论上是无穷个
• 离散属性：该属性可以取有限或可数无限个不同的值
• 分类属性：
  • 特殊的离散属性，即离散属性的一个细分类别
  • 取值是一些符号或事物的名称，每个值代表某种类别、编码或状态，并且这些值之间不存在大小或顺序关系
  • 例如：单身、已婚、离异、丧偶
• 二元属性
  • 分类属性的一种特殊情况
  • 这种属性只取两种可能的值或只能处于两个状态之一
  • 例如：1或0，布尔属性
• 序数属性
  • 离散属性的一种
  • 它所有可能的取值之间可以进行排序，虽然任意两个相距值之间的差值是未知的
  • 例如：其他<学士<硕士<博士
• 数值属性
  • 一种定量属性，也看作是一种连续属性
  • 它的取值是可以度量的，一般用整数或实数值表示
  • 数值属性可以是区间标度或比率标度属性
    • 区间标度属性：用相等的单位尺度度量。区间属性的值是有序的，可正、0、负
    • 比率标度属性：具有固有零点的数值属性，它弥补了区间标度无固定0点的不足，故可有一个值是另一个的倍数（或比率）

Q3. 相似度与相异度

相似度

• 非负有界性：0<=s(X_i,X_j)<=1，当X_i=X_j时，s(X_i,X_j)=1
• 对称性

相异度

关系： 当d(X,Y) != 0时，s(X,Y) = 1/d(X,Y)

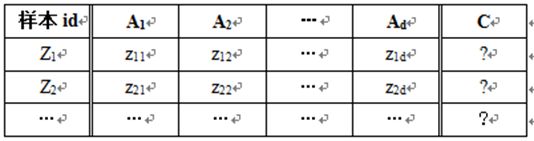
Q4. 数值属性的距离

明可夫斯基距离

当r取不同的值时，上述距离公式就特化为一些常用的距离公式

• 若r=1，则得绝对值距离公式，就称曼哈坦距离：
  
• 若r=2，则得欧几里得距离，也简称为欧氏距离：
  
• 若r->∞，称切比雪夫距离：
  

二次型距离
设A是n阶非负定矩阵，则向量X_i与X_j的二次型距离定义为：

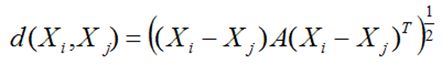
Q5. 分类属性的相似度

简单匹配系数相似度（二元相似度）

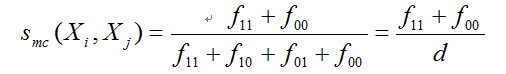
Jaccard系数相似度（非对称的二元相似度）

Rao系数相似度（非对称的二元相似度）

---

例子：试计算s_mc(X₁,X₂)，s_jc(X₁,X₂)和s_rc(X₁,X₂)

Q6. 序数属性的相似度

序数属性的值之间具有实际意义的顺序或排位，但相继值之间的差值是未知的，可用m_k表示第k个属性的可能取值有状态

计算方式：例子
假设某校用考试成绩、奖学金和月消费 3个属性来描写学生在校的信息（下表）。其中第1个属性考试成绩取m₁=5个状态，其 顺序排位为优秀>良好>中等>及格>不及格；第2个属性奖学金取m₂=3个状态，其 顺序排位为甲等>乙等>丙等 ；第3个属性月消费取m₃=3个状态，其顺序排位为高>中>低

序数属性的数据对象之间相异度计算的基本思想是将其转换为数值型属性，并用距离函数来计算，主要分为三个步骤：

• 将第k个属性的域映射为一个整数的排位集合，即将每个数据对象X_i对应分量的取值x_ik用其对应排位数代替并仍记为x_ik
• 将整数表示的数据对象Xi的每个分量映射到[0, 1]实数区间之上，其映射方法为 z_ik=(x_ik-1)/(m_k-1)
• 根据实际情况选择一种距离公式，计算任意两个数值型数据对象X_i和X_j的相异度

答：
考试成绩的域为 {优秀, 良好, 中等, 及格, 不及格} ，其整数排位集合为{5, 4, 3, 2, 1}，同理可得下图

将其映射到0~1区间内

选用欧几里得距离函数计算任意两点之间的相异度

同理可得：d(X₁,X₃)=1.22， d(X₂,X₃)=0.56

所以 从计算结果可知d(X₂,X₃)的值是最小的，即X₂与X₃的差异度最小

Q7. 余弦相似度

对数值型或属性值用数字表示的数据集中任意两个数据对象X_i=(x_i1,x_i2,…,x_in)和X_j=(x_j1,x_j2,…,x_jn)，其余弦(cosine)相似度定义为：

• X_i*X_j表示两个向量的内积
• ||Xi||表示向量X_i的欧几里得范数，即X_i到坐标原点的距离，也就是向量X_i的长度

当s_cos(X_i,X_j)=0，即向量X_i和X_j呈90°夹角，也就是说它们是相互垂直的，亦即它们是不相似的
当s_cos(X_i,X_j)=1，即向量X_i和X_j的方向是一致的，它们的方向是完全相似的

余弦相似度常常用来评价文档间的相似性。每一个文档通常用一个词频向量(term-frequency vector)来表示，每个属性为文档中可能出现的特定词或短语，属性取值为该词或短语在文档中出现的频度

Q8. 混合属性的相异度

若数据集S={X₁ ,X₂, …X_m}的属性既有数值属性，又有离散属性时，称S为混合属性数据集
处理方法：

• 假设S有d个属性
• 根据第k属性的类型，计算S关于第k属性的相异度矩阵D^(k)(S) (k=1,2,…,d)
• 将其集成为S的相异度矩阵D(S)，公式如下：
  
  • 相异度d^(k)(X_i,X_j)的取值都在 [0, 1]内
  • 第k属性是分类或二元属性时，比较X_i和X_j在第k属性的取值
    • 如果x_ik=x_jk，则d^(k)(X_i,X_j)=0，否则d^(k)(X_i,X_j)=1
  • 当第k属性是数值属性时，先求出S第k属性所有非缺失值的最大值max_k和最小值min_k，则有
    
  • 当第k属性是序数属性时
    • 先将X_i的第k属性值转换为[0,1]区间的实数z_ik=(x_ik-1)/(m_k-1)，其m_k是X第ｋ属性排位数的最大值，x_ik是X_i的第k属性值对应的排位数
    • 用z_ik和z_jk代替上述公式中的x_ik和x_jk即可

注意：

---

例题：设有下表所示的混合属性数据集S，试计算其相异度矩阵

从上表可知，数据集S除顾客id外，共有4个属性。下面分别计算S关于第1、第2、第3和第4属性的相异度矩阵

第1属性“性别”是二元属性，其的相异度矩阵

第2属性“婚姻状况”是分类属性，其相异度矩阵

第3属性“当月消费额”是数值属性，其相异度矩阵

第4属性“学位”是序数属性

• 首先转换成排位数
  
• 再将排位数转换为[0,1]区间的实数
  
• 得其相异度矩阵
  

最后

提醒：若有null值，则在计算相异度时 该项直接忽略即可

课后练习题

4. 设有5个分类属性，3个属性对象的数据集，试计算s(X₁, X₂)和s(X₁, X₃)和s(X₂, X₃)

注意：第一个s(X₁, X₂)=1/5，上图错写成2/5了

5. 设某校用考试成绩、奖学金和月消费 3个属性来描写学生在校的信息（见表7-15）。其中第1个属性考试成绩取m₁=5个状态，其 顺序排位为优秀>良好>中等>及格>不及格；第2个属性奖学金取m₂=3个状态，其顺序排位为甲等>乙等>丙等；第3个属性月消费取m₃=3个状态，其顺序排位为高>中>低，试按照序数属性相似度计算方法求s(X₁, X₂)和s(X₁, X₃)和s(X₂, X₃)

7. 设有混合属性数据集（见表7-16），试计算S的相异度矩阵

ch08 关联规则挖掘

课内重点

Q1. 关联规则挖掘的概念

支持度

---

最小支持度

---

关联规则

---

关联规则X $\Rightarrow$ Y的支持度

---

频繁项集

---

最大频繁项集

---

置信度

---

最小置信度

---

强关联规则

Q2. 四个重要定理

• 定理1（频繁项集性质1）：如果X是频繁项集，则它的任何 非空子集X’ 也是频繁项集，即频繁项集的子集必是频繁项集
• 定理2（频繁项集性质2）：如果X是非频繁项集，那么它的所有超集都是非频繁项集，即非频繁项集的超集也是非频繁项集
• 定理3（关联规则性质1）
  
• 定理4（关联规则性质2）
  

Q3. 关联规则的Apriori算法

步骤：

• 发现频繁项集
  根据用户给定的最小支持度MinS，寻找出所有的频繁项集，即满足支持度Support不低于MinS的所有项集。由于这些频繁项集之间有可能存在包含关系，因此，我们可以只关心所有的最大频繁项集，即那些不被其他频繁项集所包含的所有频繁项集
• 生成关联规则
  根据用户给定的最小可信度MinC，在每个最大频繁项集中，寻找置信度Confidence不小于MinC的关联规则

计算：发现频繁项集

计算：生成关联规则

Q4. FP-增长算法的背景

Apriori算法存在两方面的不足

• 产生大量的候选项集
  例如，当事务数据库有10⁴个频繁1-项集时，Apriori算法就需要产生多达10⁷个候选2-项集，即对存储空间要求会影响算法的执行效率
• 多次重复地扫描事务数据库
  对每个k=1,2,3,…,m，为了计算候选k-项集的支持度，都需要扫描一次事务数据库，才能确定候选k-项集的支持度，其计算时间开销很大

Q5. FP-增长算法的计算过程

用FP-增长（Frequent-Pattern Growth，FP-Growth）算法来发现频繁项集。算法只需扫描事务数据库两次，其计算过程主要由以下两步构成：

• 构造FP-树
• 生成频繁项集

举例说明：构造FP-树
对下表所示的事务数据库T，假设最小支持数MinS=2，试构造它的FP-树

冒号后面的数字代表有多少个事务含有该商品，例如 a:8，代表有8个事务中含有商品a

注意：上图仅仅是了解如何构造fp树，对于该题并没有做完，还需要进行剪枝（即满足最小支持数为2）

Q6. 提升度

• 提升度（lift） 是一种简单的相关性度量
• 对于项集A和B，如果概率P(A$\bigcup$B) = P(A)P(B)，则A和B是相互独立的，否则它们就存在某种依赖关系
• Lift(A,B)=P(A$\bigcup$B)/(P(A))$\times$P(B))=(P(A$\bigcup$B)/P(A))/P(B)
• Lift(A,B)=Confidence(A$\Rightarrow$B)/Support(B)
• 如果Lift(A,B)的值大于1表示二者存在正相关，而小于1表示二者存在负相关。若其值等于1，则表示二者没有任何关系

课后练习题

8. 设有交易数据库如表8-17所示，令MinS=0.3，试用Apriori算法求出其所有的频繁项集 + 9. 对如表8-17所示的交易数据库，令MinC=0.6，试在习题8所得频繁项集的基础上，求出所有的强关联规则

10. 设有交易数据库如表8-18所示，令MinS=0.3，试用Apriori算法求出其所有的频繁项集 + 11. 对如表8-18所示的交易数据库，令MinC=0.6，试在习题10所得频繁项集的基础上，求出所有的强关联规则

ch09 分类规则挖掘

课内重点

Q1. 数据分类的目的

从历史数据记录中自动地推导出已知数据的趋势，使其能够对未来的新数据进行预测

Q2. 分类规则挖掘

• 通过对由分类标号的训练集进行分析处理（称为有监督的学习），找到一个数据分类函数或分类模型（也称为分类器）
• 对训练集以外的、没有分类标号的任意样本点Z_u，该模型都能够将其映射到给定类别集合中的某一个类别，即给出Z_u可能的类别标号

Q3. 分类分析的三个步骤

• 挖掘分类规则（建立分类器或分类模型）
• 分类规则评估
• 分类规则应用

---

具体内容：
挖掘分类规则

• 先将一个已知类别标号的数据样本集（也称为示例数据库）随机地划分为训练集S（通常占2/3） 和 测试集T两部分
• 通过分析S中的所有样本点（数据对象），为每个类别做出准确的特征描述，或建立分类模型，或挖掘出分类规则。这一步也称为有监督的学习，即 在模型建立之前就被告知每个训练样本
• 定义：对于给定的训练样本数据集S和分类属性C=$\{$C₁,C₂,…,C_k$\}$，如果能找到一个函数f 满足以下条件，则称函数f为分类器，或分类规则，或分类方法，器寻找过程称为分类规则挖掘
  • f: S$\to$C，即f是S到C的一个映射；
  • 对于每个X_i$\in$S存在唯一C_j使f(X_i)=C_j，并记C_j= $\{$ X_i | f(X_i)=C_j，1$\le$j$\le$k，X_i $\in$ S $\}$

分类规则评估

• 对测试集T中的样本点，若有N个样本点被分类模型正确地分类，则分类模型在测试集T上的准确率定义为 “正确预测数/预测总数”，即准确率=N/|T|
• 由于T中的样本点已有分类标识，很容易统计分类器对T中样本进行正确分类的准确率，加之T中样本是随机选取的，且完全独立于训练集S，其测试准确率高就说明分类模型是可用的
• 若直接使用训练集S进行评估，则其评估结果完全可能是乐观的，即准确率很高，但因为分类模型是由S学习而得到的，它会倾向于过分拟合训练集S，而对S以外的其他数据对象进行分类却可能很不准确。因此，交叉验证法来对模型进行评估是更合理的方法

分类规则应用

• 如果评估分类模型的准确率可以接受，接下来就是利用这个分类器对没有类别标号的数据集Z进行分类
  
• 即从Z中任意取出一个样本点Z_u，将其输入分类器，得到的类别标号就是Z_u所属的类别集合

Q4. k-最近邻分类法

• k-最近邻（k-Nearest Neighbour,KNN）分类法是一种基于距离的分类算法，它既不需要事先建立分类模型，也无需对分类模型进行评估，而仅利用有类别标号的样本集，直接对没有类别标号的数据对象Z_u进行分类，即确定其类别标号
• 假定样本集S中每个数据点都有一个唯一的类别标号，每个类别标识C_j中都有多个数据对象。对于一个没有标识的数据点Z_u，k-最近邻分类法遍历搜索样本集S，找出距离Z_u最近的k个样本点，即k-最近邻集N，并将其中多数样本的类别标号分配给Z_u

例题
设某公司现有15名员工的基本信息，包括其个子为高个、中等、矮个的分类标识

公司现刚招进一位名叫刘萍的新员工Z₁，令k=5，试采用k-最近邻分类算法判断员工刘萍的个子属于哪一类？

解：

• 只有身高才是与个子高矮相关的属性，因此用X_i表示第i个员工的身高
• 首先从X中选择5个员工作为初始k-最近邻集N。不失一般性，取N={X₁=1.60，X₂=2.00，X₃=1.90，X₄=1.88，X₅=1.70}
• 对S的X₆=1.85，身高X₂=2.00是N中与身高Z₁=1.62 差距最大的员工，且有d(Z₁,X₂)>d(Z₁,X₆)，因此，在N中用X₆ 替换 X₂得到N={X₁=1.60，X₆=1.85 ，X₃=1.90，X₄=1.88，X₅=1.70}
• 同理，用S中X₇=1.59 替换 N中身高距离Z₁=1.65最大的员工X₃=1.90，得到N={X₁=1.60，X₆=1.85，X₇=1.59，X₄=1.88，X₅=1.70}
• 用X₈=1.70 替换 N中距离Z₁最大的员工X₆=1.85，得到N={X₁=1.60，X₈=1.70，X₇=1.59，X₄=1.88，X₅=1.70}
• 因为S中的X₉=2.20和X₁₀=2.10，故根据算法，N 不需要改变
• 用X₁₁=1.8 替换 N中X₄=1.88得N={X₁=1.60，X₈=1.70，X₇=1.59，X₁₁=1.80，X₅=1.70}；
• 因为S中的X₁₂=1.95，X₁₃=1.90，X₁₄=1.80，故N 不需要改变
• 用X₁₅=1.75 替换 N中X₁₁=1.8得N={X₁=1.60，X₈=1.70，X₇=1.59，X₁₅=1.75，X₅=1.70}；
• 由上所得N中，有5个身高最接近Z₁=1.62的员工，且其X₁=1.60，X₈=1.70，X₇=1.59， X₅=1.70这4个员工的类别都是“矮个”，仅有X₁₅=1.75的类别是“中等”；因此，新员工Z1=刘萍的个子为矮个

Q5. 决策树的概念

决策树是一棵有向树，也称为根树，它由矩形结点、椭圆型结点和有向边构成。

• 根结点（root node），用矩形表示，如“天气”结点，它没有入边，但有零条或多条出边。其中的字串“天气”是样本集属性名称
• 内部结点（internal node），用矩形表示。如“温度”结点，它恰有一条入边，但有两条或多条出边。“温度”是样本集属性名称
• 叶结点（leaf node）或终结点（terminal node），用椭圆表示，如“是”结点，恰有一条入边，但没有出边。椭圆形里的“是”等字符串是样本集的一个类别标号
• 每条有向边都用其出点的属性值标记，如“晴天”，“多云”、“雨天”是其出点“天气”属性的三种取值

通常，一个属性有多少种取值，就从该结点引出多少条有向边，每一条边代表属性的一种取值

Q6. Hunt算法

Hunt算法是Hunt等人1966年提出的决策树算法，它在选择划分训练集的属性时采用贪心策略，将训练集相继划分成较纯（包括更少类别）的子集，以递归方式建立决策树，并成为许多决策树算法的衍生框架，包括ID3、C4.5等

假设结点h对应的样本集用S_h表示，而C=$\{$C₁,C₂,…,C_k$\}$是其类别属性，则Hunt算法的递归定义如下：

• 如果S_h中所有样本点都属性同一个类C_h，则h为叶结点，并用分类标号C_h标记该结点
• 如果S_h中包含多个类别的样本点，则选择一个 “好” 的属性A，以属性A命名h并作为一个内部结点
• 按照属性A的取值将S_h划分为较小的子集，并为每个子集创建A的子结点
• 把A的每个子结点作为h结点，递归地调用Hunt算法

Hunt算法的停止

• 简单策略：分裂结点直到所有的记录都属于同一个类，或者所有的记录都具有相同的属性值
• 其他策略：在实际过程中还可能出现其他情况，应该考虑其它的标准来提前终止决策树的生长过程，如下所示：
  • 子结点为空
  • 训练集S_h属性值完全相同，但类别标号却不同

Q7. ID3分类方法

• ID3分类算法以信息论的信息熵为基础，以信息增益度为“属性测试条件”，并选择信息增益最大的属性对训练集进行分裂，从而实现数据的归纳分类
• 熵：最早来源于统计热力学，它是热力学系统混乱程度的一种度量。系统的混乱程度越低，其熵值就越小
• 优点
  • 模型理解容易：可方便地提取“如果-则”形式的分类规则
  • 噪声影响较小：信息增益计算使用当前的所有训练样本，可以降低个别错误样本点带来的影响
  • 分类速度较快，对未知类别标号的样本Z_u，只需从树根开始搜索一条分裂属性值与Z_u对应属性值相等的一条路径，即可对Z_u分类
• 缺点
  • 只能处理离散属性数据
  • 不能处理有缺失的数据
  • 仅是局部最优的决策树：ID3采用贪心算法，结果非全局最优
  • 偏好取值种类多的属性：ID3采用信息增益作为选择分裂属性的度量标准，但大量的研究分析与实际应用发现，信息增益偏向于选择属性值个数较多的属性，而属性取值个数较多的属性并不一定是最优或分类能力最强的属性

Q8. C4.5算法

C4.5算法不仅继承了ID3算法的优点，并增加了对连续型属性和属性值空缺情况的处理，对树剪枝也使用了当时更为成熟的方法

Q9. 贝叶斯分类方法

贝叶斯（Bayes）分类方法是以贝叶斯定理为基础的一系列分类算法的总称。贝叶斯定理就是以研究者Thomas Bayes的姓氏命名的，他是一位英国牧师，也是18世纪概率论和决策论的早期研究者之一

• 朴素贝叶斯分类器
• 树扩展的朴素贝叶斯分类器
• 贝氏增强网络朴素贝叶斯分类器
• 贝叶斯多网分类器
• 一般贝叶斯网络分类器