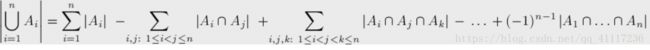容斥定理与抽屉原理

目录

【容斥定理】

【抽屉原理】

---

【容斥定理】

在计数时，为了使重叠部分不被重复计算，人们研究出一种新的计数方法，这种方法的基本思想是：先不考虑重叠的情况，把包含于某内容中的所有对象的数目先计算出来，然后再把计数时重复计算的数目排斥出去，使得计算的结果既无遗漏又无重复，这种计数的方法称为容斥原理。

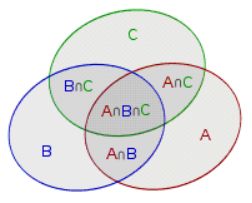
要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

【简单应用】

http://120.78.128.11/Problem.jsp?pid=2332

电灯泡

TimeLimit:1000MS  MemoryLimit:128MB

64-bit integer IO format:%lld

Problem Description

V_Dragon有n栈电灯泡，编号为1-n，每个灯泡都有一个开关。那么问题来了

1. 所有灯泡初始时为不亮的

2. V_Dragon分别进行三次操作

3. 每次操作他都选一个质数x，将编号为x和x的整数倍的灯泡的开关都拨动一下（如果灯为亮，那么拨动以后灯为不亮,如果灯不亮，拨动以后变为亮）

求最后亮着的灯的数量

Input

输入T表示T组测试数据（1<=T<=100）

接下来T组测试数据

每组第一行一个n表示灯泡个数（1<=n<=10^9）

第二行三个数a,b,c表示V_Dragon每次选择的数（1<=a,b,c<=10^6）（a,b,c全为质数且a,b,c两两互不相等）

不懂格式的同学可以参考以下格式：

Output

数组最后亮着的灯的个数

SampleInput

1 30 2 3 5

SampleOutput

15

【题解】

题意就是求A∪B∪C-A∩B-A∩C-B∩C+A∩B∩C的部分。

【代码】

#include
int main()
{
    int t,n;
    int a,b,c;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        scanf("%d%d%d",&a,&b,&c);
        int sum=n/a+n/b+n/c-2*(n/a/b+n/b/c+n/a/c)+4*(n/a/b/c);
        printf("%d\n",sum);
    }
    return 0;
}

【抽屉原理】

桌上有十个苹果，要把这十个苹果放到九个抽屉里，无论怎样放，我们会发现至少会有一个抽屉里面放两个苹果。这一现象就是我们所说的“抽屉原理”。 抽屉原理的一般含义为：“如果每个抽屉代表一个集合，每一个苹果就可以代表一个元素，假如有n+1或多于n+1个元素放到n个集合中去，其中必定至少有一个集合里有两个元素。” 抽屉原理有时也被称为鸽巢原理（“如果有五个鸽子笼，养鸽人养了6只鸽子，那么当鸽子飞回笼中后，至少有一个笼子中装有2只鸽子”）。它是组合数学中一个重要的原理。

第一抽屉原理：

原理1： 把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。

原理2 ：把多于mn(m乘n)+1（n不为0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。

原理3 ：把无穷多件物体放入n个抽屉，则至少有一个抽屉里 有无穷个物体。

第二抽屉原理：

把（mn－1）个物体放入n个抽屉中，其中必有一个抽屉中至多有（m—1）个物体。

【简单应用】

http://acm.nyist.edu.cn/JudgeOnline/problem.php?pid=417   （555这oj还有小心心的真可爱）

死神来了

时间限制：1000 ms  |  内存限制：65535 KB

难度：3

输入

有多组测试数据，不多于10000;
每组有两个数n,m;
以文件结束符EOF为结束标志。

输出

输出"YES"或"NO"。

样例输入

100 80
100 20

样例输出

YES
NO

描述

有一天，小王子在遨游世界时，遇到了一场自然灾害。一个人孤独的在一个岛上，没有吃的没有喝的。在他饥寒交迫将要死亡时，死神来了。由于这个死神在成神之前是一个数学家，所以他有一个习惯，会和即死之人玩一个数学游戏，来决定是否将其灵魂带走。游戏规则是死神给小王子两个整数n（100<=n<=1000000）,m(2<=m<=n)，在1~n个数中，随机取m个数,问在这m个数中是否一定存在一个数是另一个数的倍数，是则回答“YES",否则”NO"。如果小王子回答正确，将有再活下去的机会。但是他很后悔以前没有好好学习数学，小王子知道你数学学得不错，请你救他一命。

【代码】

#include
main()
{
    int n,m;
    while(~scanf("%d%d",&n,&m))
    {
        if(m>n/2+(n&1))
            printf("YES\n");
        else
            printf("NO\n");
    }
}