树状数组(单点修改+区间修改)
【引入】
树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和,但是每次只能修改一个元素的值;经过简单修改可以在log(n)的复杂度下进行范围修改,但是这时只能查询其中一个数组的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。
这种数据结构(算法)并没有C++和Java的库支持,需要自己手动实现。在Competitive Programming的竞赛中被广泛的使用。树状数组和线段树很像,但能用树状数组解决的问题,基本上都能用线段树解决,而线段树能解决的树状数组不一定能解决。相比较而言,树状数组效率要高很多,实现起来也比较简单。
【原理】
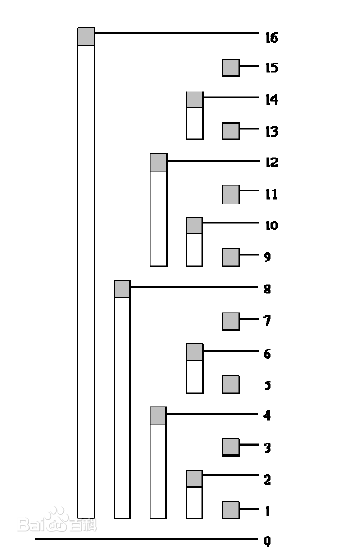
如下图所示,树状数组就是巧妙的进行二进制拆分存储元素之和,从而达到提高求和的效率的目的。
首先,我们先来了解一下lowbit(),这个函数的功能就是求某一个数的二进制表示中最低的一位1.举个栗子,x=6,二进制表示为110,那么lowbit(x)就能返回2。
二进制的视角:一个数n,假设n = 6,它的二进制为110,我们把它表示成累加的形式110 = 100 + 10,这样是可以的,那么我们要求前6(110)项的和是不是可以这样求:
∑(i=1,6)=(arr1+arr2+arr3+arr4)+(arr5+arr6)
注意括号中的元素个数,是不是4(100)个加2(010)个,和110=100+10是不是很像,10就是lowbit(110)的结果,100是lowbit(100)的结果。求和的时候我们总是把∑(i=1,n)拆分成这样的几段区间和来计算,而如何去确定这些区间的起点和长度呢?就是根据n的二进制来的,二进制怎么拆的,你就怎么拆分,而拆分二进制就要用到上面说的lowbit函数了。
【实现代码】
#include
using namespace std;
//一维
int c[100005];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,int v)
{
while(x<=n){
c[x]+=v;
x+=lowbit(x);
}
}
int query(int x)
{
int res=0;
while(x){
res+=c[x];
x-=lowbit(x);
}
return res;
}
//二维
int c[301][301];
int lowbit(int x)
{
return x&(-x);
}
void update(int x,const int &y,const int &v)
{
for(;;x<=n;x+=lowbit(x))
for(int j=y;j<=n;j+=lowbit(j))
c[x][j]+=v;
}
int getsum(int x,const int &y)
{
int res=0;
for(;x;x-=lowbit(x))
for(int j=y;j;j-=lowbit(j))
res+=c[x][j];
return res;
}
【例题】hdu 1166 敌兵布阵
【...】树状数组其实就是单点修改,区间查询。那么区间修改呢?下面我们来引入题目详细讲解。
【题目】
Color the ball
TimeLimit: 9000/3000 MS (Java/Others) MemoryLimit: 32768/32768 K (Java/Others)
64-bit integer IO format:%I64d
Problem Description
N个气球排成一排,从左到右依次编号为1,2,3....N.每次给定2个整数a b(a <= b),lele便为骑上他的“小飞鸽"牌电动车从气球a开始到气球b依次给每个气球涂一次颜色。但是N次以后lele已经忘记了第I个气球已经涂过几次颜色了,你能帮他算出每个气球被涂过几次颜色吗?
Input
每个测试实例第一行为一个整数N,(N <= 100000).接下来的N行,每行包括2个整数a b(1 <= a <= b <= N)。
当N = 0,输入结束。
Output
每个测试实例输出一行,包括N个整数,第I个数代表第I个气球总共被涂色的次数。
SampleInput
3
1 1
2 2
3 3
3
1 1
1 2
1 3
0SampleOutput
1 1 1
3 2 1【题解】
题意:区间修改,单点查询。
思路:这道题可以把每次染色的点抽象为每次涂改的区间,然后对要查询的点所在区间的更新次数进行求和,这样就可以在时间上大大缩短,查询和统计的时间复杂度都为log(n)。
树状数组中的每个节点都代表了一段线段区间,每次更新的时候,根据树状数组的特性可以把b以前包含的所有区间都找出来,全部加一次染色次数,然后再把a以前的区间全部减一次染色次数。这样就修改了树状数组中的[a,b]的区间染色次数,查询每一个点总的染色次数的时候,就可以直接向上统计每个父节点的值,就是包含这个点的所有区间被染色次数。这就是树状数组中向下查询,向上统计的典型应用。
【代码】
#include
#include
#define lowbit(x) (x&-x)
const int MAXN=100010;
int n,c[MAXN];
void update(int x,int v)
{
while(x>0){
c[x]+=v;
x-=lowbit(x);
}
}
int query(int x)
{
int ret=0;
while(x<=n){
ret+=c[x];
x+=lowbit(x);
}
return ret;
}
main()
{
int a,b,i;
while(scanf("%d",&n),n){
memset(c,0,sizeof(c));
for(i=0;i 【题目】
题目描述 Description
给你N个数,有两种操作:
1:给区间[a,b]的所有数增加X
2:询问区间[a,b]的数的和。
输入描述 Input Description
第一行一个正整数n,接下来n行n个整数,再接下来一个正整数Q,每行表示操作的个数,如果第一个数是1,后接3个正整数,
表示在区间[a,b]内每个数增加X,如果是2,表示操作2询问区间[a,b]的和是多少。
输出描述 Output Description
对于每个询问输出一行一个答案
样例输入 Sample Input
3
1
2
3
2
1 2 3 2
2 2 3
样例输出 Sample Output
9
数据范围及提示 Data Size & Hint
数据范围
1<=n<=200000
1<=q<=200000
【题解】
题意:区间修改,区间查询。
思路:观察式子:
a[1]+a[2]+...+a[n] = (c[1]) + (c[1]+c[2]) + ... + (c[1]+c[2]+...+c[n]) = n*c[1] + (n-1)*c[2] +... +c[n]
= n * (c[1]+c[2]+...+c[n]) - (0*c[1]+1*c[2]+...+(n-1)*c[n]) ---> 式子①
那么我们就维护一个数组c2[n],其中c2[i] = (i-1)*c[i],每当修改c1的时候,就同步修改一下c2,这样复杂度O(logN)就不会改变。
那么式子①=n*query(c1,n) - query(c2,n)
【代码】
#include
#define lowbit(x) (x&-x)
#define ll long long
#define maxn 200010
using namespace std;
ll n,q,c1[maxn],c2[maxn],num[maxn];
void add(ll *r, ll pos, ll v)
{
for(;pos<=n;pos+=lowbit(pos))
r[pos]+=v;
}
ll query(ll *r, ll pos)
{
ll ans=0;
for(;pos;pos-=lowbit(pos))
ans+=r[pos];
return ans;
}
main()
{
ll i, j, type, a, b, v, sum1, sum2;
scanf("%lld",&n);
for(i=1;i<=n;i++){
scanf("%lld",num+i);
add(c1,i,num[i]-num[i-1]);
add(c2,i,(i-1)*(num[i]-num[i-1]));
}
scanf("%lld",&q);
while(q--){
scanf("%lld%lld%lld",&type,&a,&b);
if(type==1){
scanf("%lld",&v);
add(c1,a,v);add(c1,b+1,-v);
add(c2,a,v*(a-1));add(c2,b+1,-v*b);
}
else{
sum1=(a-1)*query(c1,a-1)-query(c2,a-1);
sum2=b*query(c1,b)-query(c2,b);
printf("%lld\n",sum2-sum1);
}
}
}