【机器学习系列】之决策树剪枝和连续值、缺失值处理数学公式计算

作者：張張張張
github地址：https://github.com/zhanghekai
【转载请注明出处，谢谢！】

【机器学习系列】之“西瓜数据集”决策树构建数学公式计算过程
【机器学习系列】之决策树剪枝和连续值、缺失值处理数学公式计算
【机器学习系列】之ID3、C4.5、CART决策树构建代码

一、剪枝处理

​ 剪枝(pruning)是决策树学习算法对付“过拟合”的主要手段，可通过主动去掉一些分支来降低过拟合的风险。

• “预剪枝(prepruning)：”预剪枝是指在决策树生成过程中，对每个节点在划分前先进行估计，若当前节点的划分不能带来决策树泛化性能提升，则停止划分并将当前节点标记为叶节点。

• “后剪枝(postpruning):”后剪枝则是先从训练集生成一颗完整的决策树，然后自底向上地对非叶节点进行考察，若将该结点对应的子树替换为叶节点能带来决策树泛化性能提升，则将该子树替换为叶节点。

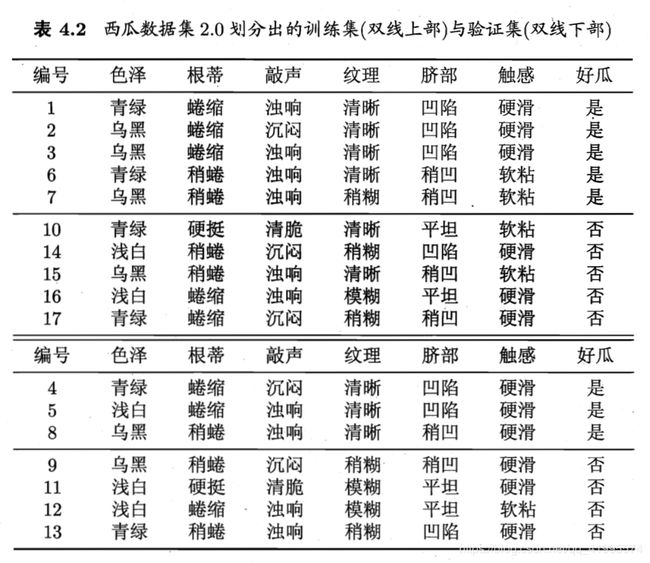
  本节采用“留出法”，预留一部分数用作“验证集”以进行性能评估，实验数据采用周志华《机器学习》一书中的“西瓜数据集”，如下表所示。

  

  假定采用信息增益准则来进行划分特征选择，则从表4.2的训练集将会生成一颗决策树，如下图所示，为了便于讨论，我们对图中的部分节点做了编号。
  

  注意事项：

  • 先通过信息曾增益确定选择的特征
  • 再计算精度，决定是否继续划分此节点（未用特征划分前的精度，与使用特征划分后的精度，进行比较）
  • 若决定不划分该特征，则将该特征下的属性设置为叶节点，节点类别为属性数据集中类别最多的类别（若正、反类别数量相等，则可任意设置），类别标记用的是训练集数据
  • 由于决策树的建立是深度优先，若决定不继续划分当前特征，则需要往回遍历
  • 剪枝操作用到了测试集！即在构建树的过程中，一边用训练集构建，一边用验证集剪枝。
  • 剪枝操作计算的是验证集在叶子节点上的精度（决策树的建立及特征的选择是在训练集上；节点精度的计算是在验证集上）
  • $测试精度=\frac{验证集正确划分数据个数}{验证集数据总数}$
  • 根节点与总验证数据集的精度比较，其余特征节点与其父特征节点精度相比较

1.预剪枝

​ 预剪枝判断的标准是看划分前后的泛化性能是否有提升：如果划分后泛化性能有提升则划分；否则，不划分。

1. 经过信息增益计算后，第（1）个节点选择的特征是“脐部”：

   ★划分前：a。所有样本都在根节点，把该节点标记为叶节点，其类别标记为训练集中样本数量最多的类别，假设这个节点标记为好瓜。

   ​ b。用验证集对其性能进行评估，{4，5，8}被正确分类，其他被错误分类，因此精度为$\frac{3}{7}\times 100$

   
   ★划分后：

   使用“脐部”特征划分后，将其下的属性标记为叶节点，类别分别为“好瓜”，“”好瓜“，”坏瓜“。此时验证集中编号为{4，5，8，11，12}的样本被正确分类，验证集精度为$\frac{5}{7}\times 100$，所以，用”脐部“进行划分。

   

2. 计算信息增益，对节点（2）进行数据划分，选取信息增益最大的特征，经计算后选择”色泽“特征。

   ★划分前：划分前的精度为该节点父节点的精度，即”脐部“特征的精度，为71.4%。

   ★划分后：

   使用“色泽”特征划分后，将其下的属性标记为叶节点，类别分别为“好瓜”，“”好瓜“，”坏瓜“。此时验证集中编号为{4，8，11，12}的样本被正确分类，验证集精度为$\frac{4}{7}\times 100$，所以，不使用”色泽“特征划分，将该节点设置为叶子节点。

   

3. 计算信息增益，对节点（3）进行数据划分，选取信息增益最大的特征，经计算后选择”根蒂“特征。

   ★划分前：划分前的精度为该节点父节点的精度，即”脐部“特征的精度，为71.4%。

   ★划分后：使用“根蒂”特征划分后，将其下的属性标记为叶节点，类别分别为“坏瓜”，“”好瓜“，”好瓜“。此时验证集中编号为{4，5，8，11，12}的样本被正确分类，验证集精度为$\frac{5}{7}\times 100$，该节点精度与其父节点精度相同，这个划分不能提升验证集精度，所以，不使用”根蒂“特征划分，将该节点设置为叶子节点。

   

4. 计算信息增益，对节点（4）进行数据划分，由于其所含训练样本已属于同一类，所以不再进行划分，将其设置为叶节点

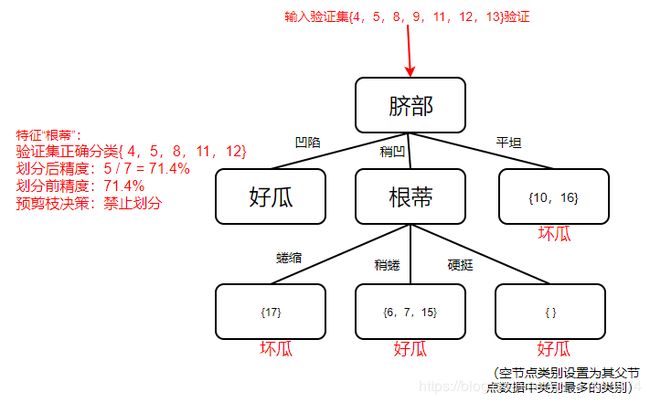
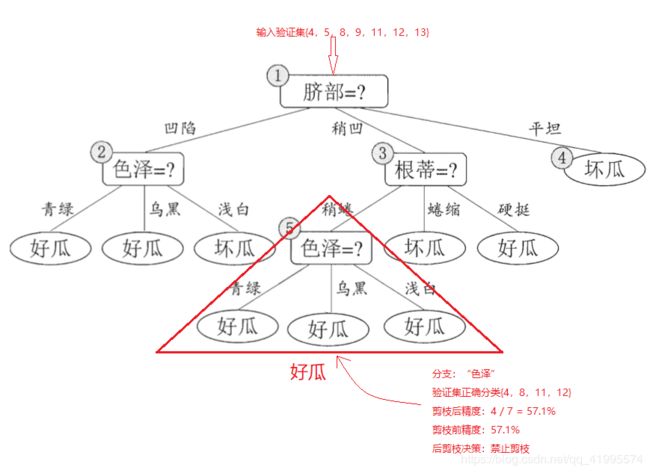
综上所述，经”预剪枝“操作后，生成的决策树如下图所示，其验证精度为71.4%。

总结：预剪枝使得决策树的很多分支都没有“展开”，这不仅降低了过拟合的风险,还显著减少了决策树的训练时间开销和测试时间开销.但另一方面,有些分支的当前划分虽不能提升泛化性能、甚至可能导致泛化性能暂时下降,但在其基础上进行的后续划分却有可能导致性能显著提高；预剪枝基于“贪心”本质禁止这些分支展开，给预剪枝决策树带来了欠拟合的风险。

2.后剪枝

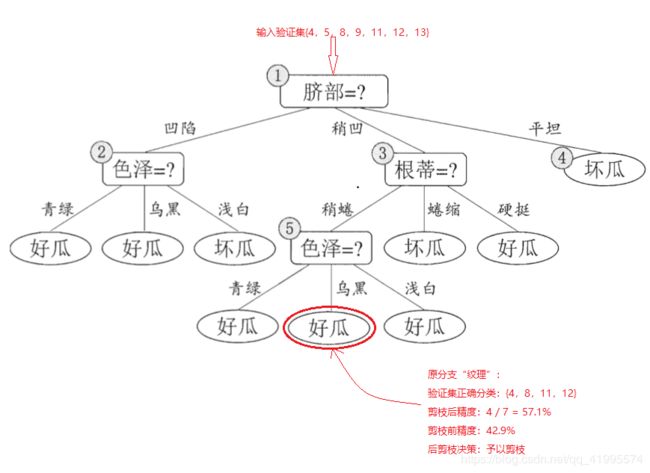
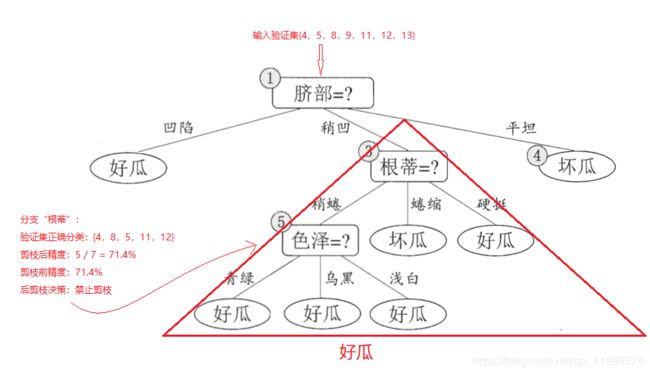
后剪枝先从训练集生成一颗未剪枝的完整的决策树，如下图所示，然后自底向上的对非叶节点进行考察，若将该节点对应的子树转换为叶节点能够带来泛化性能的提升，即精度提升，则把该节点设置为叶子节点。

1. 传入验证集，此时验证集中编号为{4，11，12}的样本被正确分类，该决策树的验证集精度为$\frac{3}{7}\times 100$

   

2. 后剪枝算法首先考察上图中的节点（6），若将以其为根节点的子树删除，即相当于把节点（6）替换为叶节点，替换后的叶节点包括编号为{7，15}的训练样本，因此把该叶节点类别设置为”好瓜“，此时验证集中编号为{4，8，11，12}的样本被正确分类，验证集精度为$\frac{4}{7}\times 100$，所以将该节点进行剪枝，将其设置为叶节点。

   

3. 然后考察节点（5），将其领衔的子树替换为叶节点，则替换后的叶节点包含编号为{6，7，15}的训练数据，叶节点类别表记为”好瓜“，此时验证集中编号为{4，8，11，12}的样本被正确分类，验证集精度为$\frac{4}{7}\times 100$，精度并没有提升，于是可以不进行剪枝。
   

4. 对节点（2），若将其领衔的子树替换为叶节点，则替换后的叶节点包含编号为{1，2，3，14}的训练数据，叶节点标记为好瓜，此时验证集中编号为{4，5，8，11，12}的样本被正确分类，验证集精度为$\frac{5}{7}\times 100$,所以将该节点进行剪枝，将其设置为叶节点。

   

5. 对节点（3），若将其领衔的子树替换为叶节点，则替换后的叶节点包含编号为{6，7，15，17}的训练数据，叶节点标记为好瓜，此时验证集中编号为{ 4，5，8，11，12 }的样本被正确分类，验证集精度为$\frac{5}{7}\times 100$，精度并没有提升，于是可以不进行剪枝。

   

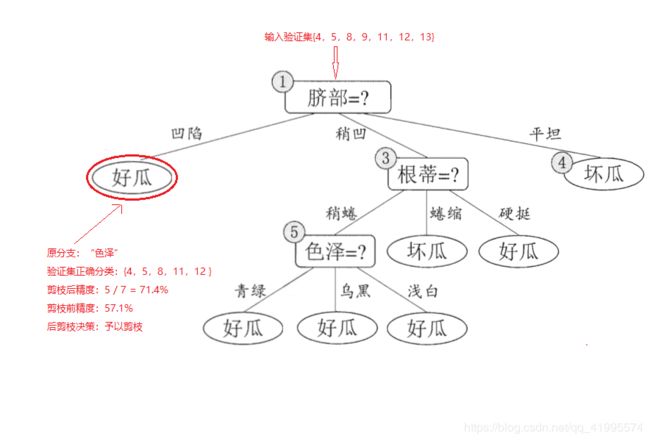
6. 对节点（1），若将其领衔的子树替换为叶节点，则替换后的叶节点包含编号为{1，2，3，6，7，10，14，15，16，17}的训练数据，叶节点标记为好瓜，此时验证集中编号为{ 4，5，8 }的样本被正确分类，验证集精度为$\frac{5}{7}\times 100\%=42.9\%<71.4\%$，精度未得到提高，所以不进行剪枝。

最终基于后剪枝策略从表4.2数据所生成的决策树如下图所示，其验证集精度为71.4%。

总结：
1.后剪枝决策树的欠拟合风险很小，泛化西宁嗯往往优于预剪枝决策树。但后剪枝过程是在生成完全决策树之后进行的，并且要自底向上地对树中的所有非叶节点进行逐一考察，因此其训练时间开销比未剪枝决策树和预剪枝决策树都要大得多。

2.预剪枝决策树精度没有提升，则进行剪枝操作；

​ 后剪枝决策树精度没有提升，则不进行剪枝操作；

​ 原因：减少多余的操作。

二、连续与缺失值

1.连续值处理

由于连续属性的可取值数目不再有限，因此，不能直接根据连续属性的可取值来对节点进行划分。此时，最简单的策略时采用“二分法（bi-partition）”对连续属性进行处理。

处理操作：给定样本集D和连续属性a，假定a在D上出现了n个不同的取值，将这些值从小到大进行排序，记为$a^1，a^2，...，a^n$。基于划分点 t 可将D分为子集$D_t^{—}$和$D_t^{+}$，其中$D_t^{—}$包含哪些在属性a上取值不大于 t 的样本，而$D_t^{+}$则包含哪些在属性a上取值大于 t 的样本。因此，对连续属性a，我们可考察包含n - 1个元素的候选划分点集合：
$$T_a=\{\frac{a^i+a^{i+1}}{2}|1\le i\le n-1\}$$
即把区间$[a^i，a^{i=1})]$的中位点$\frac{a^i+a^{i+1}}{2}$做为候选划分点。然后，我们就可以像离散属性值一样来考察这些划分点，选取最优的划分点进行样本集合的划分。

我们以增添了两个连续属性“密度”和“含糖率”的西瓜数据集为例，如下表所示，用这个数据集来生成一颗决策树。

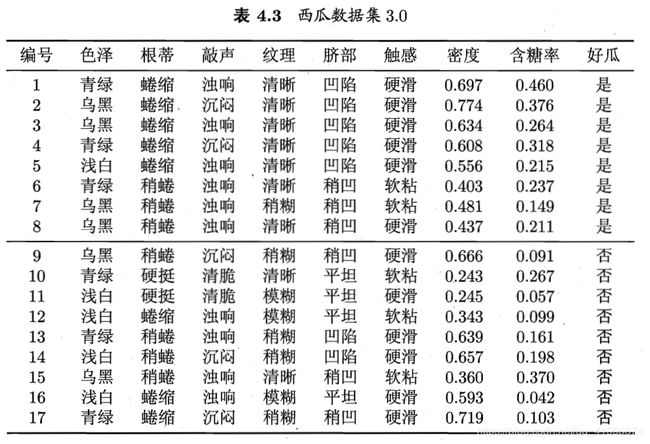
以信息增益构造树的规则为例：

将根节点视为叶节点时的信息增益为：
$$Ent(D)=-\sum _{k=1}^2{p}_{k}lo{g}_2{p}_k=-(\frac{8}{17}lo{g}_2\frac{8}{17}+\frac{9}{17}lo{g}_2\frac{9}{17})=0.998$$
★特征“密度”：

1. 决策树开始学习时，根节点包含的17个训练样本在“密度”特征上取值均不同。我们先把“密度”这些值从小到大排序：

   $T_{sort}=\{0.243，0.245，0.343，0.360，0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

2. 根据上面$T_a$的计算公式，，依次计算相邻两位的平均值，计算好后总计 n - 1 位：

   $T_{mid}=\{0.244,0.294,0.351,0.381,0.420,0.459,0.518,0.574,0.600,0.621,0.636,0.648,0.661,0.681,0.708,0.746\}$

3. $⨀$当 t = 0.244时：

   $D_t^{—}=\{0.243\}$

   $D_t^{+}=\{0.245，0.343，0.360，0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

   $Ent(D_t^{—})=-(0lo{g}_{2}0+1lo{g}_{2}1)=0$

   $Ent(D_t^{+})=-(\frac{8}{16}lo{g}_2\frac{8}{16}+\frac{8}{16}lo{g}_2\frac{8}{16})=1$

   $\therefore Gain(D,密度,0.244)=0.998-(\frac{1}{17}\times 0+\frac{16}{17}\times 1)=0.057$

   $⨀$当 t = 0.294时：

   $D_t^{—}=\{0.243，0.245\}$

   $D_t^{+}=\{0.343，0.360，0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

   $Ent(D_t^{—})=-(0lo{g}_{2}0+\frac{2}{2}lo{g}_2\frac{2}{2})=0$

   $Ent(D_t^{+})=-(\frac{8}{15}lo{g}_2\frac{8}{15}+\frac{7}{15}lo{g}_2\frac{7}{15})=0.997$

   $\therefore Gain(D,密度,0.294)=0.998-(\frac{2}{17}\times 0+\frac{15}{17}\times 0.997)=0.118$

   $⨀$当 t = 0.351时：

   $D_t^{—}=\{0.243，0.245，0.343\}$

   $D_t^{+}=\{0.360，0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

   $Ent(D_t^{—})=-(0lo{g}_{2}0+\frac{3}{3}lo{g}_2\frac{3}{3})=0$

   $Ent(D_t^{+})=-(\frac{8}{14}lo{g}_2\frac{8}{14}+\frac{6}{14}lo{g}_2\frac{6}{14})=0.985$

   $\therefore Gain(D,密度,0.351)=0.998-(\frac{3}{17}\times 0+\frac{14}{17}\times 0.985)=0.187$

   $⨀$当 t = 0.381时：

   $D_t^{—}=\{0.243，0.245，0.343，0.360\}$

   $D_t^{+}=\{0.403，0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

   $Ent(D_t^{—})=-(0lo{g}_{2}0+\frac{4}{4}lo{g}_2\frac{4}{4})=0$

   $Ent(D_t^{+})=-(\frac{8}{13}lo{g}_2\frac{8}{13}+\frac{5}{13}lo{g}_2\frac{5}{13})=0.961$

   $\therefore Gain(D,密度,0.381)=0.998-(\frac{4}{17}\times 0+\frac{13}{17}\times 0.961)=0.263$

   $⨀$当 t = 0.420时：

   $D_t^{—}=\{0.243，0.245，0.343，0.360，0.403\}$

   $D_t^{+}=\{0.437，0.481，0.556，0.593，0.608，0.634，0.639，0.657，0.666，0.697，0.719，0.774\}$

   $Ent(D_t^{—})=-(\frac{1}{5}lo{g}_2\frac{1}{5}+\frac{4}{5}lo{g}_2\frac{4}{5})=0.722$

   $Ent(D_t^{+})=-(\frac{7}{12}lo{g}_2\frac{7}{12}+\frac{5}{12}lo{g}_2\frac{5}{12})=0.980$

   $\therefore Gain(D,密度,0.420)=0.998-(\frac{5}{17}\times 0.722+\frac{12}{17}\times 0.980)=0.094$

   $⨀$当 t = 0.459、t= 0.518、t = 0.574 …就不再展示详细的计算过程了

   经过比较后发现，当t = 0.381时，Gain(D，a，t)最大为0.263。因此选择该划分点，此时可计算出特征“密度”的信息增益为0.263。

★特征“含糖率”：

​ 可以用同样的方法、同样的计算，计算出：

​ $当t=0.126时，Gain(D，含糖率，0.126)=0.349$

★离散特征：

​ 可以由上一篇博客“西瓜数据集”决策树构建数学公式计算过程中的方法计算到各特征的信息增益：

​ Gain(D，色泽) = 0.109 \quad\quad\quad Gain(D，根蒂) = 0.143 \quad\quad\quad Gain(D，敲声) = 0.141

​ Gain(D，纹理) = 0.381 \quad\quad\quad Gain(D，脐部) = 0.289 \quad\quad\quad Gain(D，触感) = 0.006

​ Gain(D，密度) = 0.262 \quad\quad\quad Gain(D，含糖率) = 0.349

​ 比较能够知道纹理的信息增益最大，因此“纹理”特征被选作根节点划分属性，此后节点划分过程递归进行，最终生成如下图所示的决策树。

​

注意：

1. 选择划分点时从$T_{mid}$中选；生成$D_t^{—}$ 和 $D_t^{+}$子集的时候从$T_{sort}$中选。
2. 属性是连续的特征，选取所有“划分点”中信息增益最大的划分点，作为该特征的信息增益和划分点。
3. 若当前节点划分属性为连续属性，该特征还可作为其后代节点的划分特征，只不过候选划分点集合中，去除了其父节点使用过的那个划分点为界限的一部分划分点。例：在父结点上使用了$“密度\le 0.381”$，不会禁止在子结点上使用$“密度\le 0.294”$，但其子结点上不应该也不能出现$"密度>0.381"$的划分点。

2.缺失值处理

​ 如下表所示，下表是西瓜数据集出现缺失值的版本，如果放弃不完整的样本，则仅有编号{4，7，14，16}的4个样本能被使用，显然，有必要考虑利用有缺失属性值的训练样例来进行学习。

我们需要解决两个问题：

1. 如何在特征下属性缺失的情况下进行划分特征选择？比如“色泽”这个特征有的样本在该特征下的值是缺失的，那么如何计算“色泽”特征的信息增益？
2. 给定划分特征，若样本在该特征下的值缺失，如何对样本进行划分？即：到底把这个样本划分到哪个节点里？

给定训练集$D$和特征$a$，令$\tilde{D}$表示$D$中在特征$a$上没有缺失值的样本子集。比如，假设$a="色泽"，则\tilde{D}=\{2,3,4,6,7,8,9,10,11,12,14,15,16,17\}$。

2.1 对于问题（1）

$显然我们可以根据\tilde{D}来判断特征a的优劣。可以根据\tilde{D}来计算特征a的信息增益或其他指标，再给定根据\tilde{D}计算出来的值一个权重，就可以表示D中特征a的优劣。$
问题（1）缺失值处理操作：$假定特征a下有V个可取属性\{a^1,a^2,\cdots ,a^V\},令{\tilde{D}}^v表示\tilde{D}中在特征a下的属性为a^v的样本子集，{\tilde{D}}_k表示\tilde{D}中属于第k类(k=1，2，\cdots ,|Y|)的样本子集。假定为每个数据样本x赋予一个权重w_x，并定义：$
$$\begin{gathered} \rho :表示无缺失值样本\tilde{D}在D上所占的比例； \\ {\tilde{\rho }}_k：表示无缺失值样本中第k类样本({\tilde{D}}_k)在\tilde{D}上所占的比例； \\ {\tilde{\gamma }}_v：表示无缺失值样本中特征a下的属性取值为a^v的样本({\tilde{D}}^v)在\tilde{D}上所占的比例。 \end{gathered}$$
因此可以把前面用到的信息增益公式改为：
$$\begin{gathered} Gain(D,a)=\rho \times Gain(\tilde{D},a)=\rho \times (Ent(\tilde{D})-\sum _{v=1}^V{\tilde{\gamma }}_{v}Ent({\tilde{D}}^v)) \\ Ent(\tilde{D})=-\sum _{k=1}^{|Y|}{\tilde{p}}_{k}lo{g}_2{\tilde{p}}_k \end{gathered}$$
可以把信息增益率公式改为：
$$\begin{gathered} Gain\_ratio(D,a)=\frac{Gain(D,a)}{IV(a)} \\ IV(a)=-\sum _{v=1}^V{\tilde{\gamma }}_{v}lo{g}_2{\tilde{\gamma }}_v \end{gathered}$$
可以把基尼指数公式改为：
$$\begin{gathered} Gini\_index(D,a)=\rho \times Gini\_index(\tilde{D},a)=\rho \times (\sum _{v=1}^V{\tilde{\gamma }}_{v}Gini({\tilde{D}}^v)) \\ Gini(\tilde{D})=1-\sum _{k=1}^V{\tilde{p}}_k^2 \end{gathered}$$

2.2 对于问题（2）

$若样本x在划分特征a下的属性取值未知，则将x同时划入所有子结点，且样本权值在与属性值a^v对应的子结点中调整为{\tilde{\gamma }}_v\cdot w_x。$即：让同一个样本以不同的概率划分到不同的子结点中去。

以表4.4 含有缺失项的西瓜数据集2.0$\alpha$为例构造决策树：

1. 根节点开始时包含训练集$D$中全部17个样本，每个样本权重$w_x=1$。

2. ★特征”色泽“：

该属性上无缺失值的样本子集$\tilde{D}=\{2,3,4,6,7,8,9,10,11,12,14,15,16,17\}$共14个样本，因此$\rho =\frac{14}{17}，其中正样本比例{\tilde{p}}_1=\frac{6}{14}。{\tilde{p}}_2=\frac{8}{14}，则：$
$$Ent(\tilde{D})=-\sum _{k=1}^2{\tilde{p}}_{k}lo{g}_2{\tilde{p}}_k=-(\frac{6}{14}lo{g}_2\frac{6}{14}+\frac{8}{14}lo{g}_2\frac{8}{14})=0.985$$
${\tilde{D}}^1\{色泽=青绿\}：\{4,6,10,17\}$
$Ent({\tilde{D}}^1)=-(\frac{2}{4}lo{g}_2\frac{2}{4}+\frac{2}{4}lo{g}_2\frac{2}{4})=1$

${\tilde{D}}^2\{色泽=乌黑\}：\{2,3,7,8,9,15\}$
$Ent({\tilde{D}}^2)=-(\frac{4}{6}lo{g}_2\frac{4}{6}+\frac{2}{6}lo{g}_2\frac{2}{6})=0.918$

${\tilde{D}}^3\{色泽=浅白\}：\{11，12，14，16\}$
$Ent({\tilde{D}}^3)=-(\frac{0}{4}lo{g}_2\frac{0}{4}+\frac{4}{4}lo{g}_2\frac{4}{4})=0$

$$Gain(\tilde{D}，色泽)=Ent(\tilde{D})-\sum _{v=1}^3{\tilde{\gamma }}_{v}Ent({\tilde{D}}^v)=0.985-(\frac{4}{14}\times 1+\frac{6}{14}\times 0.918+\frac{4}{14}\times 0)=0.306$$
$$Gain(D,色泽)=\rho \times Gain(\tilde{D}，色泽)=\frac{14}{17}\times 0.306=0.252$$
由上述方法可以得到其他特征的信息增益：
Gain(D,根蒂)=0.171 \quad\quad\quad Gain(D,敲声)=0.145 \quad\quad\quad Gain(D,纹理)=0.424
Gain(D,脐部)=0.289 \quad\quad\quad Gain(D,触感)=0.006
比较后发现，“纹理”在所有特征中的信息增益最大，因此，纹理被选为划分特征，用于对根结点进行划分。

此时，编号为{8，10}的样本在”纹理“这个特征上是缺失的，于是，将这两个样本同时放入到三个分支里，只不过进入到每个分支后还需要调整该编号的权重（上述说过，初始时每个样本的权重均为1）。加入缺失值后划分的决策树如下图，并显示了编号{8，10}在每个结点内的权重。

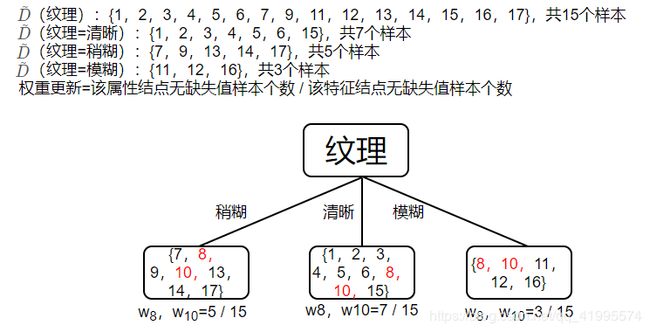
由于样本权重发生了变化，在决策树递归建立时要注意变化后的样本权重。接下来递归执行”纹理=稍糊“，样本集$D=\{7,8,9,10,13,14,17\}$

3.★特征”色泽“
$该属性上无缺失值的样本子集\tilde{D}=\{7,8,9,10,14,17\}$共6个样本，但是样本8和样本10的权重都不再是1，而是$\frac{1}{3}$，因此$\rho =\frac{4+\frac{2}{3}}{5+\frac{2}{3}}=\frac{14}{17}$，其中正样本比例${\tilde{p}}_1=\frac{1+\frac{1}{3}}{4+\frac{2}{3}}=\frac{4}{14}$，${\tilde{p}}_2=\frac{3+\frac{1}{3}}{4+\frac{2}{3}}=\frac{10}{14}$。则：
$$Ent(\tilde{D})=-\sum _{k=1}^2{\tilde{p}}_{k}lo{g}_2{\tilde{p}}_k=-(\frac{4}{14}lo{g}_2\frac{4}{14}+\frac{10}{14}lo{g}_2\frac{10}{14})=0.863$$
${\tilde{D}}^1\{色泽=乌黑\}：\{7,8,9\};{\tilde{\gamma }}_1=\frac{2+\frac{1}{3}}{4+\frac{2}{3}}=\frac{7}{14};$
$Ent({\tilde{D}}^1)=-(\frac{1+\frac{1}{3}}{2+\frac{1}{3}}lo{g}_2\frac{1+\frac{1}{3}}{2+\frac{1}{3}}+\frac{1}{2+\frac{1}{3}}lo{g}_2\frac{1}{2+\frac{1}{3}})=-(\frac{4}{7}lo{g}_2\frac{4}{7}+\frac{3}{7}lo{g}_2\frac{3}{7})=0.985$

${\tilde{D}}^2\{色泽=青绿\}：\{10，17\};{\tilde{\gamma }}_2=\frac{1+\frac{1}{3}}{4+\frac{2}{3}}=\frac{4}{14};$
$Ent({\tilde{D}}^2)=-(\frac{0}{1+\frac{1}{3}}lo{g}_2\frac{0}{1+\frac{1}{3}}+\frac{1+\frac{1}{3}}{1+\frac{1}{3}}lo{g}_2\frac{1+\frac{1}{3}}{1+\frac{1}{3}})=0$

${\tilde{D}}^3\{色泽=浅白\}：\{14\};{\tilde{\gamma }}_3=\frac{1}{4+\frac{2}{3}}=\frac{3}{14};$
$Ent({\tilde{D}}^3)=-(\frac{0}{1}lo{g}_2\frac{0}{1}+\frac{1}{1}lo{g}_2\frac{1}{1})=0$

$$Gain(\tilde{D},色泽)=Ent(\tilde{D})-\sum _{v=1}^3{\tilde{\gamma }}_{v}Ent({\tilde{D}}^v)=0.863-(\frac{7}{14}\times 0.985+\frac{4}{14}\times 0+\frac{3}{14}\times 0)=0.371$$
$$Gain(D,色泽)=\rho \times Gain(\tilde{D}，色泽)=\frac{14}{17}\times 0.371=0.305$$

由上述方法可以得到其他特征的信息增益：
Gain(D,根蒂)=0.039 \quad\quad\quad Gain(D,敲声)=0.381
Gain(D,脐部)=0.216 \quad\quad\quad Gain(D,触感)=0.291
比较后发现，“敲声”在所有特征中的信息增益最大，因此，纹理被选为划分特征，用于对该结点进行划分，划分后的决策树如下图所示。

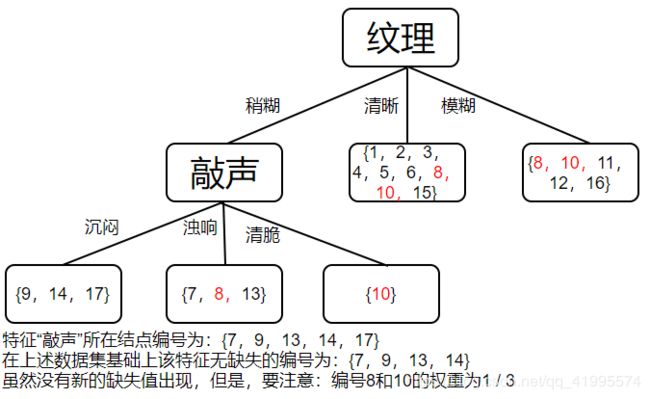
​ 4.按上述的方法经过递归操作后，最终生成的决策树如下图所示：

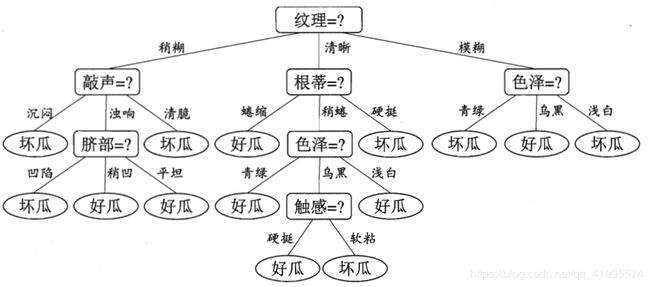
至此，决策树的部分就整理完了，回顾下第一篇博客我们讲了ID3、C4.5、CART决策的构建；第二篇博客我们讲了剪枝、连续值、缺失值的处理。接下来我会把三种决策树构建的代码整理好，并在下一篇博客中进行讲解。

【参考文献】

• 天泽28 CSDN博客：https://blog.csdn.net/u012328159/article/details/70184415
• 刘建平 博客园：https://www.cnblogs.com/pinard/
• 周志华 《机器学习》