数据结构---串（结构体实现）

目录

顺序串及其基本运算的实现

链串及其基本运算的实现

串的模式识别

BF算法（简单粗暴）

 KMP算法

改进的KMP算法

---

串(string)是由零个或多个字符组成的有限序列。kong'chuan是任何串的子串

串中所含字符的个数称为该串的长度。一般情况下，英文字母、数字和常用的变电符号以及空格符都是合法的字符。

两个串相等当且仅当它们的长度相等并且各对应位置上的字符都相同。

顺序串及其基本运算的实现

顺序串的存储方式有两种：

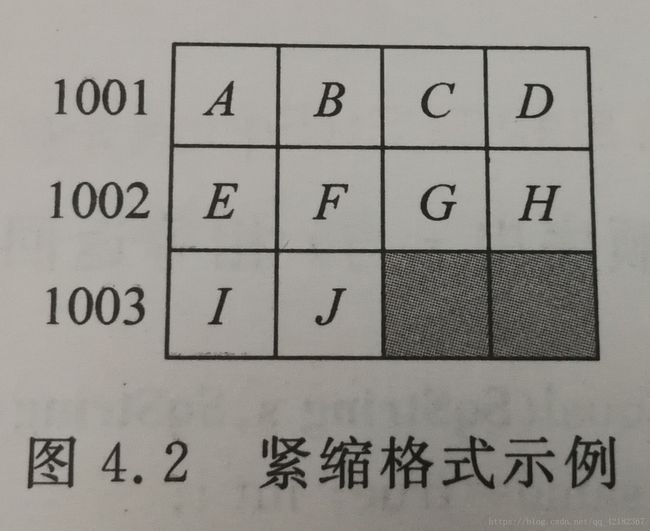
第一种，每个字只存一个字符（假设一个字包含4个字节），称为非紧缩格式（存储密度小）；

第二种，每个字存放多个字符，称为紧缩格式（存储密度大）。

非紧缩格式         紧缩格式  

顺序串参数采用直接传递顺序串的方法，不同于顺序表算法采用的是顺序表指针。

顺序串结构体声明

#define MaxSize 20
typedef struct {
	char data[MaxSize];
	int length;
}SqString;

生成串 StrAssign(&s, cstr)

将一个字符串常量（以‘\0’结尾）赋给顺序串s

void StrAssign(SqString &s, char cstr[]) {
	int i = 0;
	for (; cstr[i] != '\0'; i++)
		s.data[i] = cstr[i];
	s.length = i;
}

串的复制 StrCopy(&s, t)

void StrCopy(SqString &s, SqString t) {
	for (int i = 0; i < t.length; i++)
		s.data[i] = t.data[i];
	s.length = t.length;
}

判断串相等 StrEqual(s, t)

bool StrEqual(SqString s, SqString t) {
	bool same = true;
	if (s.length != t.length) same = false;
	else
		for (int i = 0; i < s.length; i++)
			if (s.data[i] != t.data[i]) {
				same = false;
				break;
			}
	return same;
}

串的连接 Concat(s, t)

SqString Concat(SqString s, SqString t) {
	SqString str;
	str.length = s.length + t.length;
	for (int i = 0; i < s.length; i++)
		str.data[i] = s.data[i];
	for (int i = 0; i < t.length; i++)
		str.data[s.length + 1] = t.data[i];
	return str;
}

求子串 SubStr(s, i, j)

求从第 i 个字符开始的由连续 j 个字符组成的子串

SqString SubStr(SqString s, int i, int j) {
	SqString str;
	str.length = 0;
	if (i <= 0 || i > s.length || j<0 || j>s.length - i + 1)
		return str;									//参数不正确时返回空串
	for (int k = i - 1; k < i + j - 1; k++)
		str.data[k - i + 1] = s.data[k];
	str.length = j;
	return str;
}

子串的插入 InsStr(s1, i, s2)

将顺序串s2插入到顺序串s1的第 i (i<=i<=n+1) 个位置上

SqString InsStr(SqString s1, int i, SqString s2) {
	SqString str;
	str.length = 0;
	if (i <= 0 || i > s1.length + 1) return str;
	for (int j = 0; j < i - 1; j++)
		str.data[j] = s1.data[j];
	for (int j = 0; j < s2.length; j++)
		str.data[i - 1 + j] = s2.data[j];
	for (int j = i - 1; i < s1.length; j++)
		str.data[s2.length + j] = s1.data[j];
	str.length = s1.length + s2.length;
	return str;
}

子串的删除 DelStr(s, i, j)

在顺序串中删去从第 i 个字符开始的长度为 j 的子串

SqString DelStr(SqString s, int i, int j) {
	SqString str;
	str.length = 0;
	if (i <= 0 || i > s.length || j<0 || j>s.length - i + 1)
		return str;
	for (int k = 0; k < i - 1; k++)
		str.data[k] = s.data[k];
	for (int k = i + j - 1; k < s.length; k++)
		str.data[k - j] = s.data[k];
	str.length = s.length - j;
	return str;
}

子串的替换 RepStr(s, i, j, t)

在顺序串s中将第i个字符开始的连续 j 个字符构成的子串用顺序串t替换

SqString RepStr(SqString s, int i, int j, SqString t) {
	SqString str;
	str.length = 0;
	if (i <= 0 || i > s.length || j<0 || j>s.length - i + 1)
		return str;
	for (int k = 0; k < i - 1; k++)
		str.data[k] = s.data[k];
	for (int k = 0; k < t.length; k++)
		str.data[i + k - 1] = t.data[k];
	for (int k = i + j - 1; k < s.length; k++)
		str.data[t.length + k - j] = s.data[k];
	str.length = i + t.length - 1;
	return str;
}

输出串 DispStr(s)

void DispStr(SqString s) {
	if (s.length > 0) {
		for (int i = 0; i < s.length; i++)
			cout << s.data[i] << " ";
		cout << endl;
	}
}

链串及其基本运算的实现

链串的组织形式与一般的单链表类似，主要区别在于链串中的一个结点可以存储多个字符。通常将链串中每个结点所存储的字符个数称为结点大小。这里只讨论结点大小为1的链串。

链串的结点类型 LinkNode 的声明

typedef struct snode {
	char data;
	struct snode* next;
}LinkStrNode;

生成串 StrAssign(&s, cstr)

void StrAssign(LinkStrNode* &s, char cstr[]) {
	LinkStrNode *r, *p;
	s = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = s;
	for (int i = 0; cstr[i] != '\0'; i++) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = cstr[i];
		r->next = p;
		r = p;
	}
	r->next = NULL;
}

销毁串 DestroyStr(&s)

void DestroyStr(LinkStrNode* &s) {
	LinkStrNode *pre = s, *p = s->next;
	while (p != NULL) {
		free(pre);
		pre = p;
		p = p->next;
	}
	free(pre);
}

串的复制 StrCopy(&s, t)

void StrCopy(LinkStrNode* &s, LinkStrNode *t) {
	LinkStrNode *r, *p, *q = t->next;
	s = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = s;
	while (q != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	r->next = NULL;
}

判断串相等 StrEqual(s, t)

bool StrEqual(LinkStrNode *s, LinkStrNode *t) {
	LinkStrNode *p = s->next, *q = t->next;
	while (p != NULL && q != NULL && q->data == p->data) {
		p = p->next;
		q = q->next;
	}
	if (p == NULL && q == NULL)
		return true;
	else
		return false;
}

求串长 StrLength(s)

int StrLength(LinkStrNode *s) {
	int i = 0;
	LinkStrNode *p = s->next;
	while (p != NULL) {
		i++;
		p = p->next;
	}
	return i;
}

串的连接 Concat(s, t)

LinkStrNode* Concat(LinkStrNode* s, LinkStrNode* t) {
	LinkStrNode *str, *q = s->next, *r, *p;
	str = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = str;
	while (q != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	q = t->next;
	while (q != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	r->next = NULL;
	return str;
}

求子串 SubStr(s, i, j)

求从第 i 个字符开始的由连续 j 个字符组成的子串

LinkStrNode* SubStr(LinkStrNode* s, int i, int j) {
	LinkStrNode* str, *q = s->next, *r, *p;
	str = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = str;
	if (i <= 0 || i > StrLength(s) || j<0 || i + j - 1>StrLength(s))
		return str;
	for (int k = 1; k < i; k++)
		q = q->next;
	for (int k = 1; k < j; k++) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	r->next = NULL;
	return str;
}

子串的插入 InsStr(s1, i, s2)

将顺序串s2插入到顺序串s1的第 i (i<=i<=n+1) 个位置上

LinkStrNode* InsStr(LinkStrNode* s, int i, LinkStrNode *t) {
	LinkStrNode *str, *qs = s->next, *qt = t->next, *r, *p;
	str = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = str;
	if (i <= 0 || i > StrLength(s) + 1)
		return str;
	for (int k = 1; k < i; k++) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qs->data;
		r->next = p;
		r = p;
		qs = qs->next;
	}
	while (qt != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qt->data;
		r->next = p;
		r = p;
		qt = qt->next;
	}
	while (qs != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qs->data;
		r->next = p;
		r = p;
		qs = qs->next;
	}
	r->next = NULL;
	return str;
}

子串的删除 DelStr(s, i, j)

在顺序串中删去从第 i 个字符开始的长度为 j 的子串

LinkStrNode* DelStr(LinkStrNode* s, int i, int j) {
	LinkStrNode *str, *q = s->next, *p, *r;
	str = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = str;
	if (i <= 0 || i > StrLength(s) || j<0 || i + j - 1 > StrLength(s))
		return str;
	for (int k = 1; k < i; k++) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	for (int k = 0; k < j; k++)
		q = q->next;
	while (q != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = q->data;
		r->next = p;
		r = p;
		q = q->next;
	}
	r->next = NULL;
	return str;
}

子串的替换 RepStr(s, i, j, t)

在顺序串s中将第i个字符开始的连续 j 个字符构成的子串用顺序串t替换

LinkStrNode* RepStr(LinkStrNode* s, int i, int j, LinkStrNode* t) {
	LinkStrNode *str, *qs = s->next, *qt = s->next, *p, *r;
	str = (LinkStrNode*)malloc(sizeof(LinkStrNode));
	r = str;
	if (i <= 0 || i > StrLength(s) || j<0 || i + j - 1>StrLength(s))
		return str;
	for (int k = 1; k < i; k++) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qs->data;
		r->next = p;
		r = p;
		qs = qs->next;
	}
	for (int k = 0; k < j; k++)
		qs = qs->next;
	while (qt != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qt->data;
		r->next = p;
		r = p;
		qt = qt->next;
	}
	while (qs != NULL) {
		p = (LinkStrNode*)malloc(sizeof(LinkStrNode));
		p->data = qs->data;
		r->next = p;
		r = p;
		qs = qs->next;
	}
	r->next = NULL;
	return str;
}

输出串 DispStr(s)

void DispStr(LinkStrNode* s) {
	LinkStrNode *p = s->next;
	while (p != NULL) {
		cout << p->data<<" ";
		p = p->next;
	}
	cout << endl;
}

串的模式识别

BF算法（简单粗暴）

int BF(SqString s, SqString t) {
	int i = 0, j = 0;
	while (i < s.length&&j < t.length) {
		if (s.data[i] == t.data[j]) {
			i++;
			j++;
		}
		else {
			j = 0;
			i = i - j + 1;
		}
	}
	if (j >= t.length)
		return i - t.length;
	else
		return -1;
}

 KMP算法

避免了串s的i指针的回溯

void GetNext(SqString t, int next[]) {
	int j = 0, k = -1;
	next[0] = -1;
	while (j < t.length - 1) {
		if (k == -1 || t.data[j] == t.data[k]) {
			j++;
			k++;
			next[j] = k;
		}
		else
			k = next[k];
	}
}
int KMPIndex(SqString s, SqString t) {
	int next[MaxSize], i = 0, j = 0;
	GetNext(t, next);
	while (i < s.length&&j < t.length) {
		if (j == -1 || s.data[i] == t.data[j]) {
			i++;
			j++;
		}
		else
			j = next[j];
	}
	if (j >= t.length)
		return i - t.length;
	else
		return -1;
}

改进的KMP算法

void GetNextval(SqString t, int nextval[]) {
	int j = 0, k = -1;
	nextval[0] = -1;
	while (j < t.length) {
		if (k == -1 || t.data[j] == t.data[k]) {
			j++;
			k++;
			if (t.data[j] != t.data[k])
				nextval[j] = k;
			else
				nextval[j] = nextval[k];
		}
		else
			k = nextval[k];
	}
}
int KMPIndex_val(SqString s, SqString t) {
	int nextval[MaxSize], i = 0, j = 0;
	GetNext(t, nextval);
	while (i < s.length&&j < t.length) {
		if (j == -1 || s.data[i] == t.data[j]) {
			i++;
			j++;
		}
		else
			j = nextval[j];
	}
	if (j >= t.length)
		return i - t.length;
	else
		return -1;
}