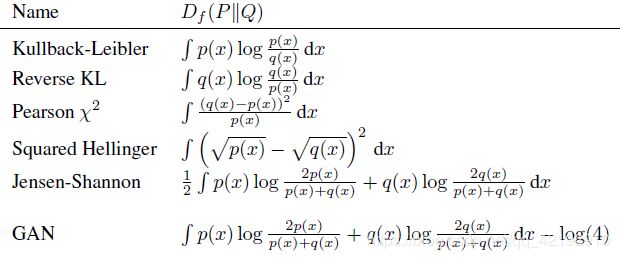f-GAN: Training Generative Neural Samplers using Variational Divergence Minimization

$f$-GAN: Training Generative Neural Samplers using Variational Divergence Minimization

Paper:http://papers.nips.cc/paper/6066-f-gan-training-generative-neural-samplers-using-variational-divergence-minimization.pdf
Tips：Nips2016的一篇paper，主要研究GAN的object function的问题。
（阅读笔记）

1.Main idea

• 提出问题：GAN的效果很好能够生成一个与目标相似的分布，但是却无法计算出某个事件的似然或者边缘似然。but cannot be used for computing likelihoods or for marginalization.
• GAN做生成只是一个特例。We show that the generative-adversarial approach is a special case of an existing more general variational divergence estimation approach.
• 任意的目标函数（散度）都能用于GAN的训练。We show that any $f$-$divergence$ can be used for training generative neural samplers.

2.Intro

• 当有了生成模型$Q$后，一般用于：
  • 抽样：从模型$Q$中抽样，可以得到重要的信息，如：做决策。
  • 估计：从$P$中得到独立同分布的样本$\{x_1,x_2,...,x_n\}$，然后可以找到$Q$相似于$P$分布。
  • 似然估计：给定$x$，估计是分布$Q$的概率。
• 原始GAN是$\mathbf{J}\mathbf{S}$散度（Details中详述），如下所示：
  $$\begin{array}{r}{D}_{\mathbf{J}\mathbf{S}}(P\Vert Q)=\frac{1}{2}{D}_{\mathbf{K}\mathbf{L}}(P\Vert \frac{1}{2}(P+Q))+\frac{1}{2}{D}_{\mathbf{K}\mathbf{L}}(Q\Vert \frac{1}{2}(P+Q))\end{array}\text{\hspace{1em}(1)}$$

3.Details

• $f$-$divergence$用于衡量两个分布$P$和$Q$之间得差距的。其中$f(\cdot )$要求：是下凸函数且$f(1)=0$，所以不同的$f(\cdot )$也就用不同的距离散度形式：
  $$\begin{array}{r}{D}_f(P\Vert Q)={\int }_{\mathcal{X}}q(x)f(\frac{p(x)}{q(x)})\mathrm{d}x\end{array}\text{\hspace{1em}(2)}$$
  其实很明显地，当$p(x)$和$q(x)$相等时，$f(\cdot )=0$，即$D_f(P\Vert Q)=0$，之间距离就为0；又$f(\cdot )$是下凸函数，也就是$f(\frac{x_1+x_2+,,,+x_n}{n})\le \frac{f(x_1)+f(x_2)+...+f(x_n)}{n}\to f(\mathbb{E}(x))\le \mathbb{E}(f(x))$，于是：
  $$\begin{array}{rl}\mathbb{E}(f(x))\ge f(\mathbb{E}(x))\to {\int }_{\mathcal{X}}q(x)f(x)\mathrm{d}x& \ge f({\int }_{\mathcal{X}}q(x)x\mathrm{d}x)\\ \to {\int }_{\mathcal{X}}q(x)f(\frac{p(x)}{q(x)})\mathrm{d}x& \ge f({\int }_{\mathcal{X}}q(x)\frac{p(x)}{q(x)}\mathrm{d}x)\\ & =f({\int }_{\mathcal{X}}p(x)\mathrm{d}x)\\ & =f(1)\\ & =0\end{array}\text{\hspace{1em}(3)}$$
  $D_f(P\Vert Q)$有下界且是其最小值0，即可用于衡量距离。
• $f$-$divergence$中的函数$f(\cdot )$有一共轭函数$f^{\ast }(\cdot )$；在当前自变量$t$值的时候，取到$f(\cdot )$定义域内所有$u$，使得$\{\cdot \}$中值最大的情况就是函数$f^{\ast }(t)$的值，如下式所示：
  $$\begin{array}{r}{f}^{\ast }(t)=\underset{u\in {\mathrm{d}\mathrm{o}\mathrm{m}}_f}{\sup }\{ut-f(u)\}\end{array}\text{\hspace{1em}(4)}$$
  $f$与$f^{\ast }$可以互相转换，即$f(u)={\sup }_{t\in {\mathrm{d}\mathrm{o}\mathrm{m}}_{f^{\ast }}}\{tu-f^{\ast }(t)\}$，所以有：
  $$\begin{array}{rl}{D}_f(P\Vert Q)& ={\int }_{\mathcal{X}}q(x)f(\frac{p(x)}{q(x)})\mathrm{d}x\\ & ={\int }_{\mathcal{X}}q(x)\underset{t\in {\mathrm{d}\mathrm{o}\mathrm{m}}_{f^{\ast }}}{\sup }\{t\frac{p(x)}{q(x)}-f^{\ast }(t)\}\mathrm{d}x\\ & \ge {\int }_{\mathcal{X}}q(x)\times (T(x)\frac{p(x)}{q(x)}-f^{\ast }(T(x)))\mathrm{d}x\\ & ={\int }_{\mathcal{X}}T(x)p(x)-q(x)f^{\ast }(T(x))\mathrm{d}x\\ & ={\int }_{\mathcal{X}}T(x)p(x)\mathrm{d}x-{\int }_{\mathcal{X}}q(x)f^{\ast }(T(x))\mathrm{d}x\end{array}\text{\hspace{1em}(5)}$$
  由上式有，因为$D_f(P\Vert Q)$要求取到所有的$t$得到的函数最大值才是最终的结果，直接替换成另一函数$T(x)$必然是更小的，即使$T(x)$是从某一函数集$\mathcal{T}$得到的最大的函数，所以找到一个很好的最大的$T(x)$就可以去逼近$D_f(P\Vert Q)$；所以上式改写如下：
  $$\begin{array}{rl}{D}_f(P\Vert Q)& \ge \underset{T\in \mathcal{T}}{\sup }\{{\int }_{\mathcal{X}}T(x)p(x)\mathrm{d}x-{\int }_{\mathcal{X}}q(x)f^{\ast }(T(x))\mathrm{d}x\}\\ & =\underset{T\in \mathcal{T}}{\sup }\{{\mathbb{E}}_{x\sim P}[T(x)]-{\mathbb{E}}_{x\sim Q}[f^{\ast }(T(x))]\}\end{array}\text{\hspace{1em}(6)}$$
  同时，$T^{\ast }(x)=f^{\prime }(\frac{p(x)}{q(x)})$，见https://arxiv.org/pdf/0809.0853.pdf中5.1节式子$(45)(46)$。
• 用$f$-$divergence$作为目标函数来训练GAN；其中$P$是真实分布，$T_{\omega }$是输入输出函数（给一输入找到最优的结果最大化$(6)$式），$Q_{\theta }$是生成器（假的分布），如下所示：
  $$\begin{array}{r}F(\theta ,\omega )={\mathbb{E}}_{x\sim P}[T_{\omega }(x)]-{\mathbb{E}}_{x\sim Q_{\theta }}[f^{\ast }(T_{\omega }(x))]\end{array}\text{\hspace{1em}(7)}$$
  正如式子$(6)(7)$所示，目标是两个分布最小化，即需要$D_f(P\Vert Q)$最小化，但是需要找到最大化$(6)$式得到最优$T(x)$才能很好衡量$D_f$，其次才对$D_f$最小化。所以训练即关于$\omega$最大化，关于$\theta$最小化。
• 需要考虑$f^{\ast }$的定义域，所以假设$T_{\omega }(x)=g_f(V_{\omega }(x))$，其中${\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{g}\mathbf{e}}_{V_{\omega }}\to \mathbb{R}$；同时${\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{g}\mathbf{e}}_{g_f}\to {\mathbf{d}\mathbf{o}\mathbf{m}\mathbf{a}\mathbf{i}\mathbf{n}}_{f^{\ast }}$，$g_f$激活函数的选择为单调递增函数：
  $$\begin{array}{r}F(\theta ,\omega )={\mathbb{E}}_{x\sim P}[g_f(V_{\omega }(x))]+{\mathbb{E}}_{x\sim Q_{\theta }}[-f^{\ast }(g_f(V_{\omega }(x)))]\end{array}\text{\hspace{1em}(8)}$$
  原始GAN的目标函数如下所示：
  $$\begin{array}{r}F(\theta ,\omega )={\mathbb{E}}_{x\sim P}[\log D_{\omega }(x)]+{\mathbb{E}}_{x\sim Q_{\theta }}[\log (1-D_{\omega }(x))]\end{array}\text{\hspace{1em}(9)}$$
  实际中其实找不到$D_{\omega }$，只能尽量去接近。
  所以参数更新即是，其中$f(\cdot )=u\log u-(u+1)\log (u+1)$：
  $$\begin{array}{rl}\{\theta ,\omega \}& =\arg \underset{G}{\min }\underset{D}{\max }{D}_f(P\Vert G_{\theta })\\ & =\arg \underset{G}{\min }\underset{D}{\max }\{{\mathbb{E}}_{x\sim P}[\log D_{\omega }(x)]+{\mathbb{E}}_{x\sim G_{\theta }}[\log (1-D_{\omega }(x))]\}\\ & \to \frac{\partial \{{\mathbb{E}}_{x\sim P}[\log D_{\omega }(x)]+{\mathbb{E}}_{x\sim G_{\theta }}[\log (1-D_{\omega }(x))]\}}{\partial D_{\omega }}\\ & =\frac{\partial \{\int p(x)\log D_{\omega }(x)\mathrm{d}x+\int g_{\theta }(x)\log (1-D_{\omega }(x))\mathrm{d}x\}}{\partial D_{\omega }(x)}\\ & \to p(x)\frac{1}{D_{\omega }(x)}-g_{\theta }(x)\frac{1}{1-D_{\omega }(x)}=0\\ & \to D_{\omega }(x)=\frac{p(x)}{p(x)+g_{\theta }(x)}\end{array}\text{\hspace{1em}(10)}$$
  将上式子再带回目标函数：
  $$\begin{array}{rl}& {\mathbb{E}}_{x\sim P}[\log \frac{p(x)}{p(x)+g_{\theta }(x)}]+{\mathbb{E}}_{x\sim G_{\theta }}[\log (1-\frac{p(x)}{p(x)+g_{\theta }(x)})]\\ & =\int p(x)\log \frac{p(x)}{p(x)+g_{\theta }(x)}\mathrm{d}x+\int g_{\theta }(x)\log (1-\frac{p(x)}{p(x)+g_{\theta }(x)})\mathrm{d}x\\ & =\int p(x)\log \frac{\frac{p(x)}{2}}{\frac{p(x)+g_{\theta }(x)}{2}}\mathrm{d}x+\int g_{\theta }(x)\log (1-\frac{\frac{p(x)}{2}}{\frac{p(x)+g_{\theta }(x)}{2}})\mathrm{d}x\\ & =\int p(x)\log \frac{p(x)}{\frac{p(x)+g_{\theta }(x)}{2}}\mathrm{d}x+\int g_{\theta }(x)\log (1-\frac{p(x)}{\frac{p(x)+g_{\theta }(x)}{2}})\mathrm{d}x-2\log 2\\ & =\mathbf{K}\mathbf{L}(P\Vert \frac{P+G_{\theta }}{2})+\mathbf{K}\mathbf{L}(G_{\theta }\Vert \frac{P+G_{\theta }}{2})-2\log 2\\ & =\mathbf{J}\mathbf{S}(P\Vert G_{\theta })-2\log 2\end{array}\text{\hspace{1em}(11)}$$
  所以整体GAN训练过程就是固定G，找D；然后固定D，找G；如$(7)$式所示。
• 用不同$f$-$divergence$作为目标函数就是不同的度量方式来衡量差距，GAN的由来可能是因为理解生成器和判别器打分形象，但是发现其实很多散度都可以用作差距。如下图所示：