二叉查找树&哈夫曼树
目录
- 二叉排序树(BST)(Binary Sort(Search)Tree)
- 二叉排序树的节点删除
- 哈夫曼树
二叉排序树(BST)(Binary Sort(Search)Tree)
- 二叉排序树的任何一个非叶子节点要求:
- 左子节点的值比当前节点的值小
- 有子节点的值比当前节点的值大
注:如果有相同的值,可以将该节点放在左子节点或右子节点
- 结构体定义
typedef struct tree_node
{
int data;
uint key;// 索引,找到key,就找到对应的信息。
// 类似于根据编号找到学生信息,用二叉排序树比链表一个一个查找编号更快了
struct tree_node *left;
struct tree_node *right;
}Node, *pNode, **ppNode;
typedef struct tree
{
pNode root;
}Tree;
- 插入节点
pNode insert_node(pNode root, pNode node)
{
if (root == NULL)
{
return NULL;
}
if (node == NULL){
return root;
}
if (root->key < node->key)
{
if (root->right == NULL)
{
link_node(node, root, 0, node->left, node->right);//0 是右边 1是左边
}
else
{
insert_node(root->right, node);
}
}
else
{
if (root->left == NULL)
{
link_node(node, root, 1, node->left, node->right);
}
else
{
insert_node(root->left, node);
}
}
return root;
}
- 链接节点
void link_node(pNode cur,pNode parent, uint isleft,pNode left, pNode right)
{
if (isleft)
{
parent->left = cur;
}
else
{
parent->right = cur;
}
cur->left = left;
cur->right = right;
}
- 根据查找值key找到节点
pNode search_node(pNode root, uint key)
{
if (root == NULL)
{
return NULL;
}
if (root->key == key)
{
return root;
}
if (root->key > key)
{
return search_node(root->left, key);
}
if (root->key < key)
{
return search_node(root->right,key);
}
}
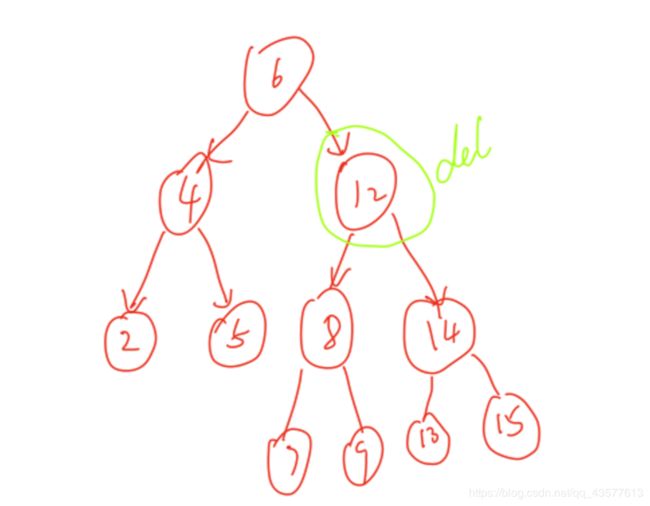
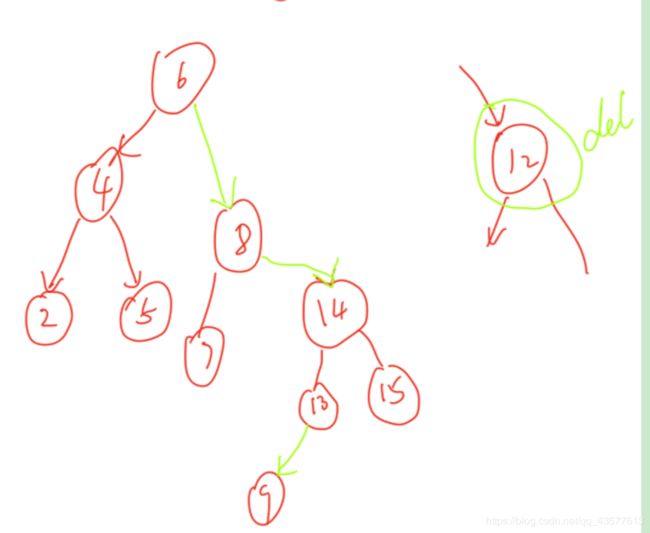
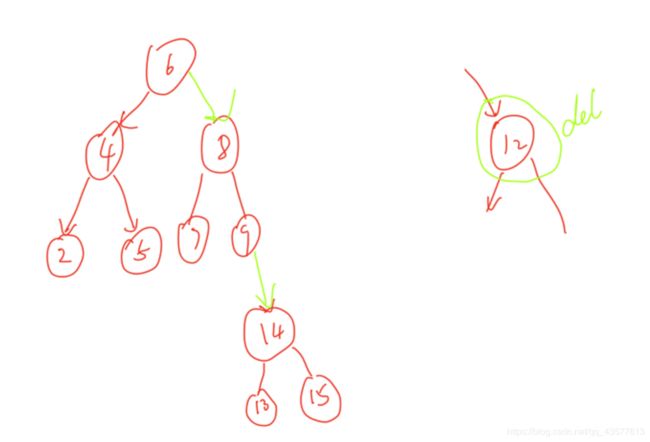
二叉排序树的节点删除
要考虑删除根的情况
pNode delete_node_in_tree(pNode root, pNode node)
{
if (root == NULL || node == NULL)
{
return root;// 删除失败
}
if (root == node)//删除根的情况
{
if (node->left == NULL && node->right == NULL)
{
root == NULL;
}
else if (node->left != NULL && node->right == NULL)
{
root = node->left;
}
else if (node->left == NULL && node->right != NULL)
{
root = node->right;
}
else
{
root = node->left;
insert_node(root,node->right);
}
delete_node(node);
node = NULL;
return root;
}
pNode parent = search_parent(root, node);
if (parent == NULL)//排除不在树里面的节点
{
return root;
}
// 留下来的是找的到父节点的
if (parent->left == node)
{
// 删除叶子节点
if (node->left == NULL && node->right == NULL)
{
parent->left = NULL;
}
// 删除有一个孩子的节点
else if (node->left != NULL && node->right == NULL)
{
parent->left = node->left;
}
else if (node->left == NULL && node->right != NULL)
{
parent->left = node->right;
}
//删除有两个孩子的节点
else
{
parent->left = node->left;
insert_node(root,node->right);
}
}
else//parent->right == node
{
if (node->left == NULL && node->right == NULL)
{
parent->right = NULL;
}
else if (node->left != NULL && node->right == NULL)
{
parent->right = node->left;
}
else if (node->left == NULL && node->right != NULL)
{
parent->right = node->right;
}
else
{
parent->right = node->left;
insert_node(root, node->right);
}
}
delete_node(node);
node = NULL;
return root;
}
哈夫曼树
- 最优二叉树
- 带权路径最小
- 一堆数据要构成哈夫曼树,所有的数据应当是叶子节点
- WPL(带权路径长度)= 节点全值*路径长度 之和
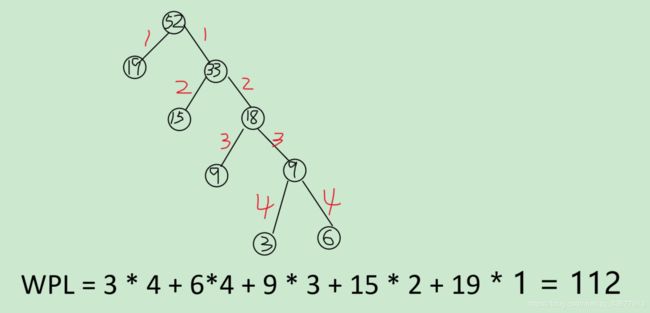
- 权值越大的点应该越靠近根,权值越小的点应该越靠近底
- 如何构建哈夫曼树
- 带权路径最小
- 同层当中小权值节点应当放在左边
- 优先级队列/堆(小数在前)
- 每次取队头两个节点组成一个和值节点从队尾放入
- 和值过后,如果队空,和值就是这棵树的根
优先级队列实现哈夫曼树
Tree *creat_huffman_tree(int *array, int len)
{
Queue *queue = create_queue();// 创建空队列
pNode node;
// 优先级队列排好序
for (int i = 0; i < len; i++)
{
node = creat_huffman_node(array[i]);
queue_enter(queue, node);
queue = priority(queue);
}
display_queue(queue);
// 每次取队头两个节点组成一个和值节点从队尾放入和
pNode left;
pNode right;
pNode root;
if (queue->length == 1)
{
root = (pNode)queue_exit(queue);
}
while (queue->length > 1)
{
left = (pNode)queue_exit(queue);
// display_queue(queue);
right = (pNode)queue_exit(queue);
// display_queue(queue);
root = creat_huffman_node(left->value + right->value);
link_node(root, left, right);
// 优先级类似于冒泡排序
queue_enter(queue, root);
// display_queue(queue);
queue = priority(queue);
// display_queue(queue);
}
destry_queue(&queue);
Tree *tree = (Tree *)malloc(sizeof(Tree));
tree->root = root;
return tree;
}
/**优先级队列**/
Queue *priority(Queue *queue)
{
if (queue->head == queue->tail)
{
return queue;
}
else
{
QNode *index = queue->tail;
int flag = 0;
while (index->prev != NULL)
{
if (((pNode)index->data)->value < ((pNode)index->prev->data)->value)
{
//交换前后两个的值
bubble_node(queue, index->prev, index);
// 调整队尾
if (flag == 0)
{
queue->tail = index->next;
flag = 1;
}
}
else
{
return queue;
}
}
// 调整队头
queue->head = index;
}
return queue;
}
void bubble_node(Queue *queue, QNode *prev, QNode *cur)
{
if (prev->prev != NULL)
{
prev->prev->next = cur;
}
cur->prev = prev->prev;
prev->prev = cur;
prev->next = cur->next;
if (cur->next != NULL)
{
cur->next->prev = prev;
}
cur->next = prev;
}
堆实现哈夫曼树*
Tree *creat_huffman_tree(int *array, int len)
{
pNode nodes[len];
for (int i = 0; i < len; i++)
{
nodes[i] = creat_huffman_node(array[i]);
}
// 创建小根堆
build_heap(nodes, len);
display_heap(nodes, len);
pNode left;
pNode right;
pNode root;
if (len == 1)
{
root = nodes[0];
}
while (len > 1)
{
// 连续两次取出小根节点,合并后再加入堆中
left = nodes[0];
// printf("left = %d \n", nodes[0]->value);
nodes[0] = nodes[--len];
heapify(nodes, len, 0);
// display_heap(nodes, len);
right = nodes[0];
// printf("right = %d \n", nodes[0]->value);
nodes[0] = nodes[--len];
// display_heap(nodes, len);
root = creat_huffman_node(left->value + right->value);
link_node(root, left, right);
// 入堆
nodes[len++] = root;
// printf("root in = %d", root->value);
build_heap(nodes, len);
// printf("rebuild");
// display_heap(nodes, len);
// printf("min = %d \n", nodes[0]->value);
}
Tree *tree = (Tree *)malloc(sizeof(Tree));
tree->root = root;
return tree;
}
/**堆**/
void swap(pNode tree[], int a, int b)
{
pNode temp;
temp = tree[a];
tree[a] = tree[b];
tree[b] = temp;
}
//堆化
void heapify(pNode tree[], int numbersize, int root)
{
int left = 2*root + 1;
int right = 2*root + 2;
int min = root;
if (left < numbersize && tree[min]->value > tree[left]->value)
{
min = left;
}
if (right < numbersize && tree[min]->value > tree[right]->value)
{
min = right;
}
if (min != root)
{
swap(tree, min, root);
//递归保证子树也是堆,这个非常关键
heapify(tree, numbersize, min);
}
}
//建立堆
void build_heap(pNode tree[], int numbersize)
{
if (numbersize > 1)
{
int last_node = numbersize - 1;
int parent = (last_node - 1) / 2;
for (int root = parent; root >= 0; root--)
{
heapify(tree, numbersize, root);
}
}
}
6.哈夫曼树的插入和删除