【CodeForce 1343E】 Weights Distributing

原题链接：https://codeforces.ml/contest/1343/problem/E

想去水一波d3，看到E题是图论，直接开始..

结果自信满满的交上去 瞬间runing on test21 直接退出(蜜汁自信)

再一看wa29是什么鬼？

再以后便没有了以后

 

题目大意：

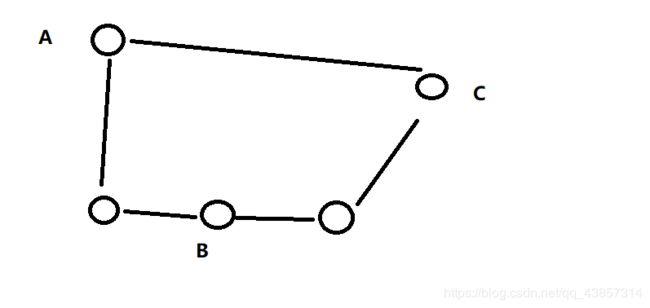
给出n个点，m条边，点a,b,c，m个待分配的边的权值

请你分配这m个边权，使得a->b,b->c的路径总权值最小

题目思路及过程：

sort排序没得说，最后把边权按权分配即可

剩下的我在想，首先(a,b)间最短路，其次(b,c)最短路，两条路都要走。

那么(a,b)与(b,c)即有重边，将重边的权值赋为最小，其次要找尽可能多的重边。

所以 ： wa29...

其实一下就可以hack掉，中转点完全不一定为b

显然A->C->B->C比A->B->C一共经过的边少

所以也就启示，每个点都可以成为中转点，然后就A了..

从a,b,c分别为起点跑最短路 得到da,db,dc数组

枚举时 :

显然红边贡献为2，具体怎么整贡献 ，不多解释了(被这题卡了 ...我fw)

Code:

/*** keep hungry and calm CoolGuang!***/
#pragma GCC optimize(2)
//#pragma GCC optimize("Ofast","unroll-loops","omit-frame-pointer","inline")
#include 
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
typedef pair pp;
const ll INF=1e18;
const int maxn=1e6+6;
const int mod=1e9+7;
const double eps=1e-9;
inline bool read(ll &num)
{char in;bool IsN=false;
in=getchar();if(in==EOF) return false;while(in!='-'&&(in<'0'||in>'9')) in=getchar();if(in=='-'){ IsN=true;num=0;}else num=in-'0';while(in=getchar(),in>='0'&&in<='9'){num*=10,num+=in-'0';}if(IsN) num=-num;return true;}
ll n,m,p;
ll num[maxn];
int head[maxn];
struct node{
    int e,next;
    ll w;
}edge[maxn];
ll cnt=0;
void addedge(int u,int v){
    edge[cnt]=node{v,head[u],0ll};
    head[u]=cnt++;
}
ll da[maxn],db[maxn],dc[maxn];
void bfs(int s,ll *dis){
    queueq;
    for(int i=1;i<=n;i++) dis[i]=INF;
    dis[s]=0;
    q.push(s);
    while(!q.empty()){
        int u = q.front();q.pop();
        for(int i=head[u];~i;i=edge[i].next){
            int e=edge[i].e;
            if(dis[e]>dis[u]+1){
                dis[e]=dis[u]+1;
                q.push(e);
            }
        }
    }
}
ll s[maxn];
int main(){
    int T;scanf("%d",&T);
    while(T--){
        ll a,b,c;
        cnt=0;
        read(n);read(m);read(a);read(b);read(c);
        for(int i=0;i<=2*m+1;i++) head[i]=-1,edge[i].w=0;
        for(int i=1;i<=m;i++) read(num[i]);
        for(int i=1;i<=m;i++){
            int x,y;scanf("%d%d",&x,&y);
            addedge(x,y);
            addedge(y,x);
        }
        s[0]=0;
        sort(num+1,num+1+m);
        for(int i=1;i<=m;i++) s[i]=s[i-1]+num[i];
        bfs(a,da);
        bfs(b,db);
        bfs(c,dc);
        ll ans=INF;
        for(int i=1;i<=n;i++){
            if(da[i]+db[i]+dc[i]>m) continue;
            ans=min(ans,s[db[i]]+s[da[i]+db[i]+dc[i]]);
        }
        printf("%lld\n",ans);
    }
    return 0;
}
/**
4
5 5
1 3 5
1 2 3 4 5
1 2
2 3
3 4
4 5
5 1
**/