LOAM论文和程序代码的解读

目的

　　LOAM是KITTI测试中排名第一的状态估计和激光建图方法，知名度很高，在它的基础上衍生出了很多改进版本，例如LEGO-LOAM、LLOAM、ALOAM、Inertial-LOAM等。
　　本文对论文和代码的细节进行分析，试图弄明白这个方法的特点以及为何有如此优秀的性能。

1　特征点提取

　　通过匹配每帧激光点云与上一帧点云，可以得到两帧之间机器人的相对位移，这是激光里程计的工作方式。传统的方法是直接在原始的点云上操作（例如ICP算法），但是LOAM采用了更巧妙的方法，它不是直接对大量的点云进行变换，而是在点云的基础上提取出相对较少的特征点，然后再用特征点进行匹配。
　　如何得到特征点呢？特征点是具有一定特征的点，对于点云中任意一个点$X$，给它定义一个特征值，称为$c$，如下式所示。其中，$X_i$ 是$X$相邻的几个点，在程序中选取的是$X$前5个和后5个。这里暗含着一个前提还没说，就是点云中的点都是按照一定顺序排列的（激光雷达返回的点就是这样的），如果点的排列顺序是杂乱无章的，再使用这个公式就没什么用了。原作者考虑激光雷达的每帧点云数据由很多独立的线组成。因此，在定义特征点时考虑的是单个线上的点与相邻点的关系。点也可看成一个向量，$||X||$表示向量的范数，也就是向量的长度，或者说点到雷达坐标系原点的距离。公式中除以$||X||$的原因是考虑到不同距离下得到的激光点的分布疏密程度不一样，为了归一化。

$$c=\frac{1}{||X||}||\sum _i(X-X_i)||$$

　　这篇论文中的公式不多，我们挨个仔细探讨，尽量做到充分理解无死角。有人将上式定义的$c$称为曲率，这么叫确实有道理。我们可以想一想，如果点$X$在一条直线上而且直线上的点都是均匀分布的，那么不管这条直线方向如何，$X$的前5个点和后5个点的平均值刚好就是$X$（此时$c=0$）。上面公式就是在计算平均点与中间点$X$的差距，点的排列越平直差距越小，反之点排列越弯曲差距越大$c$的值就越大。下面给出两个例子来更好地展示曲率的含义。左图为平面点云的例子，其中有的点在直线上有的位于边角上，我们计算各点处的曲率。为了直观地展示曲率的大小，我用直线表示在各个点上，直线高度与曲率$c$成正比，如右图所示。越尖锐的点曲率越大，在直线上的点曲率则是0。

　　　　

　　第二个例子是由光滑的曲线轮廓生成的点云，如下图所示，这时计算的曲率如右图所示，同样是曲率越大的地方直线越高。这两个例子证明我们对上面公式的理解是正确的。作者提出用曲率信息来区分激光点，这显然是个非常大的创新点。但是我们扪心自问，这个公式并不复杂，高中生都可以理解，而且特征点的概念也并不是什么开天辟地的创新。因为在跟点云处理很相近的另一个领域——图像处理中，特征点的概念几乎是尽人皆知，而且定义是五花八门，随便拿出来一个都比这个公式要复杂的多。但是将特征点的概念推广到激光点云领域可能是作者的一大贡献。

　　　　

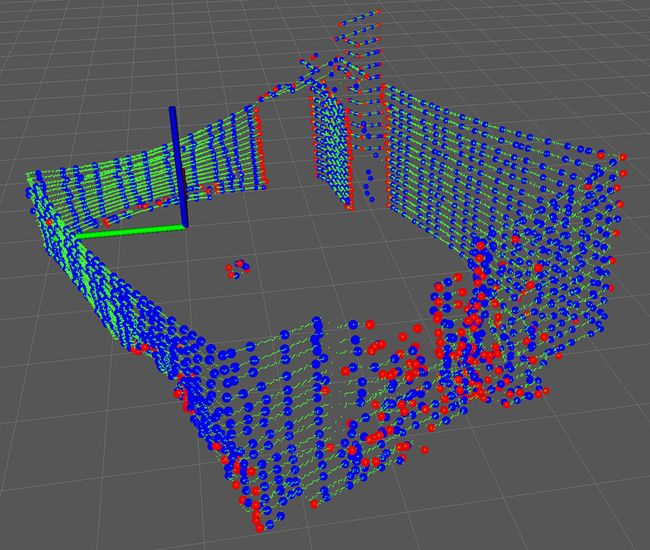
　　根据曲率值大小，可以对点进行分类。论文中分成两类：曲率大的是角点，曲率小的是平面点。其实这里叫平面点我觉得不太合适，因为提取特征是通过对每条扫描线进行计算得到的，因此应该叫“线上的点”，但是在特征匹配的时候却是用来和平面进行匹配的，这是矛盾的，但是这里不纠结这些无关紧要的细节了。下面我用实际的激光点云数据来展示特征点提取的效果。下图中的绿色点是velodyne 16线激光雷达的原始点云，扫描环境是笔者的卧室，大概就是一个长方体，能够看到点云在垂直方向大致分成了16条线。红色的小圆球是提取出来的角点，蓝色的是平面点。可见，角点基本上位于房间的墙角和过渡较大的地方，例如物体（窗帘）的边缘。但是由于程序中对特征点的数量有限制，不是所有的角点都被提取出来加以利用，可以看到四个墙角只有一个被保存下来，其它三个墙角基本上没有提取。平面点也散落在了墙壁上，同样不是所有平面点都被利用了，只有一部分。

　　在程序中，对特征点分的更细一些，除了角点和平面点，还使用了曲率$c$不太大的点（称为less sharp point），和曲率不太小的点（称为less flat point），下图中红色的小圆就是less sharp point，蓝色的小圆是less flat point。在右侧的图中我把门打开了，可以清晰地看到门口边界有更多的less sharp point。

　　对于多线激光雷达来说，计算曲率$c$是分别针对单个线进行的。但是velodyne 16线激光雷达返回的点云数据是按照先上下，后左右的顺序，如下面的动画所示。而且上下的顺序也是错杂的，至于为什么是这样的，就要问激光雷达的厂家了，我也不知道。因此在程序中需要先将其按照线号重新排列。velodyne 16雷达每次返回的数据称为一帧（sweep），一帧由16条线组成（每条线称为一个scan），每个scan有很多点。如果将velodyne 16雷达的扫描频率设置为10Hz，那么一秒就返回10帧数据。工作在10Hz的频率下，这个雷达的水平扫描角度的分辨率是0.2°，我们可以算出来理论上一帧有$360/0.2\times 16=28800$个点，但是实际上你可以试试，每次的点数不是完全一样的，有时多一点有时少一点，在程序中将存储点的数组定义为40000个元素，这是选了一个保守的上限。

2　运动估计

　　提取出特征点，下一步就是借助特征点计算两帧点云之间的相对位移，即点云匹配（或者叫配准、对齐，反正都是一个意思）。在ICP等传统匹配方法中，用点与点之间的距离评价匹配的效果，因此每个点只需要找一个对应的点，但是在LOAM采用了更好匹配标准。提取出特征点的目的是利用特征点表示环境特征，这是一种数据压缩的思想。特征点分为两类，对于角点，一般在转折线上（例如卧室里的墙角），要计算它到折线的距离；对于平面点，一般在比较平坦的表面上（例如墙面），要计算它到平面的距离。我不知道作者是怎么想到这一步的，但是应该也不会很难，拿爷爷辈的ICP方法来说，对它的改进非常多， 其中很多改进都是针对距离度量的，原始ICP使用点到点的距离度量，改进的使用点到线或者点到面（例如这篇文章[1]）。只要你看论文足够多并且善于思考、勤于联想，总能提炼出一些创新点的。
　　计算角点到折线的距离要用到点到直线的距离公式，如下式所示。其中，$X_0$是角点，直线用两个点$X_1,X_2$表示，这个公式的解释可以看这里。对比可知论文中的公式(2)是错误的，角点$X_0$只应该出现一次。这个公式也没什么难的，只要你知道一点向量点积差积和行列式的知识就行了，大学基础数学足矣。

$$d=\frac{|(X_2-X_1)\times (X_1-X_0)|}{|X_2-X_1|}$$

　　计算平面点到平面的距离要用到点到面的距离公式，如下式所示。其中，$X_0$是平面点，平面用三个不共线的点$X_1,X_2,X_3$表示，这个公式的解释可以看这里。

$$d=\frac{|((X_2-X_1)\times (X_3-X_1))\cdot (X_0-X_1)|}{|(X_2-X_1)\times (X_3-X_1)|}$$

　　LOAM使用了点到直线和点到平面来计算距离，这就意味着他适用于结构化比较好的室内环境，因为在室内环境中充满了平直的墙壁、地面、家具、平直的转折角。对于室外环境就没这么理想了，可能充满了树叶、石块、车辆等等不规则的物体，其直线和平面的假设就不太准确了。
　　LOAM还解决了运动畸变问题（叫demotion或者distortion correction）。运动畸变产生的原因就是激光雷达在采集数据的过程中是处于运动状态的。如果激光雷达的扫描频率很高，比自身的运动快得多，我们可以假设畸变很小从而忽略。但是，大多数雷达的频率都不是非常高，以velodyne 16线雷达为例，常用的频率是10Hz（最快也不过20Hz），假如机器人或者无人车的运动速度是1m/s（这算慢的了），在完成一次360°扫描的过程中雷达的位置已经改变了10cm，这就不能再忽略了。LOAM解决运动畸变的方法比较简单，就是根据每个点的相对时间进行补偿。无独有偶，我最近看百度Apollo的激光雷达运动补偿源代码的时候，发现百度也是这么简单处理的。雷达扫描一帧的时间是固定的，可以得到每个点的采集时刻，将所有点都统一到同一时刻，这里选择的是每完成一帧扫描的末尾时刻，如下图所示。$t_k$就是一帧扫描开始的时刻，$t_{k+1}$就是完成一次扫描的时刻，对于我们的例子$t_{k+1}-t_k=100$ms，水平的箭头表示将所有点都投影到$t_{k+1}$时刻。$P_k$就是这一帧扫描生成的点云，显然不同的点具有不同的时间戳。

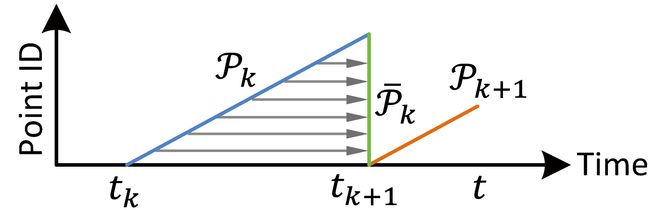
　　论文中假设雷达做最简单的运动，即匀速运动，也就是说一次扫描过程中雷达的线速度和角速度都是不变的。在时间间隔不大时，例如100ms，可以认为这样的假设比较合理。当然如果是无人机这种做剧烈运动的，这个假设就不太合理了，此时可以用IMU补偿。
　　将$t_{k+1}$时刻相对于$t_k$时刻的雷达相对位姿记为$T_{k+1}^L$，对每个特征点 $i$ 计算它的补偿变换矩阵$T_{(k+1,i)}^L$，如下式所示。这就是简单的线性插值，当然是根据匀速运动的假设来的，而且是一种近似，真正的插值可没这么简单。注意是对点云中所有的点都补偿，不仅仅是特征点，因为后面会用所有的点来建图。原公式又有个小错误，作者不太仔细啊，一共就这么几个公式还出错。

$$T_{(k+1,i)}^L=\frac{t_i-t_{k+1}}{t_k-t_{k+1}}{T}_{k+1}^L$$

　　用变换矩阵$T_{(k+1,i)}^L$对特征点 $i$ 进行变换即可完成补偿。当然具体实现还要考虑旋转变换的参数化方式，论文中使用了轴角度表示，但是在程序中却使用了欧拉角表示。

3　优化

　　别看激光点很多，上面唯一的未知量就是相对位姿$T_{k+1}^L$，我们将它视为变量，求使距离$d$最小的$T_{k+1}^L$，这可以转化成一个优化问题，然后就可以利用成熟的优化理论和方法解决了。由于特征点的变换中包含了角度的三角函数，显然这个问题是个非线性优化问题。优化目标涉及距离，因此是一个最小二乘问题。
　　最小二乘问题是一种比较常见的问题，不用害怕，有微积分的知识就能理解。我们是机器人学家不是数学家，所以不去深入探讨最小二乘方法背后的理论，会用即可。但是作为使用者，我们应该知道最小二乘问题的特点。很多从事机器人研究的年轻学者数学并不好（笔者也并不避讳这个），对问题的理解停留在人云亦云的表面，或者是知其然而不知其所以然。最小二乘问题最著名的缺点是受离群点的影响很大，下图是一个简单的例子。图中的5个黑点是数据点，假设我们想对这些数据拟合一条直线。如果采用误差的平方作为优化目标，这就是一个标准的最小二乘问题。拟合结果为图中的红色直线。如果我改变其中一个点的纵坐标，可以看到整条直线发生了严重的偏移。我移动的点就相当于实际中可能出现的离群点，这些点可能不是很多，但是仅仅几个就能严重影响解的质量。这是因为每个点的误差以平方项的形式进入方程，不难猜到，误差越大其平方项被放大的更大，为了弥补这一个很大的偏差，最小二乘法不得不牺牲其它的点。图中还展示了另一种拟合方法，这种方法使用了误差的绝对值作为优化目标，又被称为最小一乘解。可以看到，最小一乘解对离群点的包容性要好，它没有出现严重偏移。
　　为了防止结果被离群点污染，通常的做法是在求解前先剔除掉这些害群之马。

　　求解非线性最小二乘问题的常用方法有LM（ Levenberg-Marquardt）方法和高斯牛顿法。作者在论文中声称采用了LM方法，但是在程序中却使用了高斯牛顿法。不管用哪种方法，都需要计算目标函数的雅克比矩阵，这个是最繁琐的一步。雅克比矩阵由一阶导数构成，求导数可以采用数值法，也可以用解析法。数值法就是用很小的差分近似表示导数，一般用在函数复杂或者根本无法得到解析解的情况；解析法就是直接用初等函数的求导公式求出复合函数的导数，这样比较精确，作者在程序中就是直接求出导数并组装成雅克比矩阵的，他没有调用第三方的函数库。至于作者是手工求解还是用数学软件我就不知道了。
　　程序中用OpenCV自带的solve函数求解得到增量matX，不断迭代transform[i] += matX.at(i, 0);得到最优解。

cv::solve(matAtA, matAtB, matX, cv::DECOMP_QR);

　　在改进版本ALOAM中，后人就图省事直接用了Ceres库，省去了计算雅克比矩阵的工作。Ceres库是Google开发的解最小二乘问题的开源库，被用于自家的SLAM项目Cartographer。
　　求最小二乘问题的时候还有个小细节笔者一开始不太放心，就是在目标函数中涉及对应点的选择。因为对应点是根据特征点搜索得到的，也就是说依赖于特征点。如果我们改变了特征点（即使只是微小的改变），都有可能导致对应点改变，那么在求导时距离函数就不能视为不变的了。当然这只是我的理论设想 ，实际情况中大多数对应点肯定是不会特别敏感的，或者即使改变了也无所谓反正不会差太多，因此可以忽略这个问题。

4　建图

　　LOAM缺少闭环检测，它建图的主要目的还是为估计状态服务的。论文中说建图的频率与状态估计不同，比它要慢。扫描一帧就对地图做一次更新，如果用velodyne 16雷达就是10Hz，而论文中使用了简陋的自制激光雷达，建图频率只能做到1Hz。
　　建图的过程就是不断地把匹配好的点云堆积在一起的过程，其中的思路与状态估计有些类似，但是有很多地方不一样。特征点的定义和使用与前面状态估计的一样，但是数量更多了，多了10倍。为什么多了10倍大概是因为建图的频率慢了10倍吧。在寻找对应特征点时，将地图中已有的点云（$Q_k$）按照10立方米的格子存储。至于为什么是10立方米我也不知道。使用已经粗略估计出来的单帧点云（${\overline{Q}}_{k+1}$），它是相对于世界全局坐标系的。凡是与${\overline{Q}}_{k+1}$有交集的方格，从$Q_k$中取出位于这些方格中的点，再存入一个KDtree中。然后，再针对不同的特征点找它同类的那些点，${\overline{Q}}_{k+1}$中的角点找$Q_k$中对应的角点，平面点同理，各找各妈。在寻找时限制搜索范围，只找一定半径范围内的。由于现在特征点的数量增加了十倍，再挨个计算距离太慢了，此时作者采用了计算特征向量的方法。为什么用特征向量了呢？这让我们想起了另一种点云匹配方法——NDT方法。
　　特征向量的几何意义可以从下图中看出来。我生成了一些随机点，这些点都在一个椭球里面（当然不必非得是椭球，你也可以试试长方体等等）。然后再计算随机点的协方差矩阵，最后计算这个矩阵的特征值和特征向量。图中三个红色的箭头就是特征向量（更准确的说是乘以特征值后的特征向量）。可以清楚地看到，特征向量的长度反应了点的分布，也就是说我们根据特征值和特征向量就能计算出直线的方向。平面也是同理，我们可以根据两个较长的特征向量计算平面的法向量，三个向量相交于几何中心，这样平面就确定了。

　　显示以上动画的Mathematica代码如下：

Manipulate[
 pts0 = Table[{RandomReal[{-a, a}], RandomReal[{-b, b}], RandomReal[{-c, c}]}, {i, 3000}];
 pts = Select[pts0, #[[1]]^2/a^2 + #[[2]]^2/b^2 + #[[3]]^2/c^2 <= 1 &];
 cm = Covariance[pts];
 eVectors = Normalize /@ Eigenvectors@cm;
 eValues = 2*Sqrt[Eigenvalues@cm];
 Graphics3D[{Blue, Ball[#, 0.12] & /@ pts, Red, Arrowheads[0.03], Arrow[Tube[{{0, 0, 0}, #1*#2}]] & @@@Transpose@{eValues, eVectors}}, PlotRange -> 20, Axes -> True, ImageSize -> 500], Grid[{{Control[{{a, 4, Style["a", 12]}, 1, 20, 1, ImageSize -> Small}], Control[{{b, 4, Style["b", 12]}, 1, 20, 1, ImageSize -> Small}], Control[{{c, 4, Style["c", 12]}, 1, 20, 1, ImageSize -> Small}]}}], ControlPlacement -> Top, TrackedSymbols :> True]

　　然后在直线上取两个点利用前面的公式计算角点到直线的距离，在平面上取三个点计算平面点到平面的距离。后面的操作跟前面的一样，也是利用LM方法得到最优的变换，利用新得到的最优变换，将最近的一帧单帧点云叠加到地图点云之上，就完成了建图。新得到的最优变换与之前粗略估计出来的变换一般是不同的，新的变换由于使用了更多点参与计算，应该更接近真实，所以用新的变换作为以后变换的基础。这样LOAM就完成了整个状态估计和建图。整个过程没有特别复杂或者难以理解的地方，作者没有使用传统的ICP或者NDT点云匹配方法，而是自己赤手空拳发明了一种新方法。在理论上，整篇论文没有什么太难理解的东西，甚至可以说都是基础知识，既没有吓人的数学公式、也没有复杂的逻辑。当然，你得对背景有些了解，了解SLAM的一些常识、知道ICP和NDT方法的原理，大概知道它们的特点和性能表现，对于常见的数学优化方法有点了解，对于坐标变换这种基础知识掌握的比较牢靠。
　　下面我们看看程序实现上有什么值得学习的地方。

5　程序代码

　　程序代码可见LOAM_NOTED，分为四个部分。这四个部分基本是独立的，只通过ROS的消息交换数据。
　　1 scanRegistration.cpp的功能是对激光点云预处理，包括移除空点、对运动畸变补偿、计算每个点的水平和垂直角度并分成不同的scan、然后就是最重要的曲率计算、根据曲率提取出特征点，最后把特征点发布出来就不管了；
　　2 laserOdometry.cpp的功能是通过求解最小二乘问题进行点云匹配，从而得到状态估计，包括畸变补偿（上面是用IMU补偿）、查找最近的对应特征点、计算点到直线和点到平面的距离、求雅克比矩阵、迭代解最小二乘问题、最后把估计的状态发布出来就不管了；
　　3 laserMapping.cpp的功能是不断拼接每帧点云建立地图，包括对点云坐标变换、然后还是求雅克比矩阵和解最小二乘问题这一套、最后把环境地图发布出来就不管了；
　　4 transformMaintenance.cpp的功能是用第3步得到的结果矫正第2步的状态估计，得到更准确的位姿，都是一些坐标变换和相乘，没什么太复杂的，最后把矫正后的位姿发布出来就不管了；

5.1　scanRegistration代码

　　ShiftToStartIMU函数的功能是：利用IMU计算局部坐标系下点云中的点相对第一个开始点的由于加减速运动产生的位移畸变，后面用来补偿。平移的畸变如下，变量前带imu的都是IMU测量的数据。imuShiftStart是开始时刻IMU测得的当前的雷达位置，开始时刻定义成每帧扫描开始的时候，imuShiftCur是IMU测得的当前时刻的雷达位置，我只用很小一段时间内的，所以不关心累积误差。这里用了一阶速度积分来近似计算中间时刻点雷达的运动位置。

imuShiftFromStartCur = imuShiftCur - (imuShiftStart + imuVeloStart * pointTime)

　　TransformToStartIMU函数利用ShiftToStartIMU函数通过IMU得到的补偿值对点云进行补偿。先根据当前IMU测得的角度将点变换到全局坐标系，再用扫描开始时刻IMU测得的角度将点变换到激光雷达局部坐标系。
　　laserCloudHandler函数是话题调用函数，每当点云数据发布的时候就被调用。这个函数是整个文件最主要的部分，它对特征点进行了处理，其中调用了前面提到的ShiftToStartIMU、TransformToStartIMU等函数。
　　main函数就订阅velodyne_points和imu两个话题、发布laser_cloud_sharp、laser_cloud_less_sharp、laser_cloud_flat、laser_cloud_less_flat四个话题代表的特征点。main函数使用了ros::spin()而不是设置固定循环频率，这意味着它的运行频率取决于外部话题的频率。除此以外，还发布了velodyne_cloud_2话题，这是原始点云经过畸变补偿后的点云，我以后有机会对比一下看看补偿的效果怎么样。

5.2　laserOdometry代码

　　TransformToStart函数的功能与TransformToStartIMU差不多，但是后者是用IMU进行补偿、前者是用激光雷达自身估计的状态进行补偿。显然用IMU更准确、TransformToStart适用于速度比较平滑的情况。
　　main函数是主体、功能是状态估计、也可以叫里程计算。其中使用了ros::Rate rate(100)，说明这个程序的运行是固定间隔的，按照rate中设定的频率循环运行。注意这里使用了spinOnce()，要区分与spin()的不同。
　　在机器人领域，坐标系之间的变换是很常见同时也是容易出错的，即便老手也是一样。在论文和程序中采用了$z$轴朝前、$x$轴朝左、$y$轴朝上的坐标系，雷达局部坐标系$L$和全局世界坐标系$W$都是这样的，作者这样定义应该是想与相机一致，因为相机的坐标系一般定义成$z$轴朝前、垂直于镜头。而velodyne 16激光雷达默认采用的坐标系是$x$轴朝前、$y$轴朝左、$z$轴上，所以需要进行坐标变换。laserOdometry中在计算雅克比矩阵时出现了一坨坐标变换。根据这篇文章，我们知道作者采用了$Y_1{X}_2{Z}_3$欧拉角表示旋转变换，如下。至于作者为什么选择这种表达方式，我也不知道。注意旋转变换的表示方式与坐标系的定义是两码事，别搞混了。

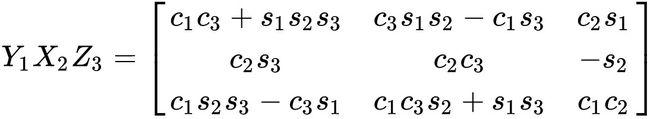
　　可以在数学软件中验证它是怎么来的，我以Mathematica软件为例，输入以下命令：

RotationMatrix["1", {0, 1, 0}].RotationMatrix["2", {1, 0, 0}].RotationMatrix["3", {0, 0, 1}] /. {Cos[x_] :>Subscript[c, x], Sin[x_] :> Subscript[s, x]} // MatrixForm

　　计算结果如下，可见与上面的公式一样。

　　掌握齐次变换矩阵的同学都知道，矩阵依次在右侧相乘表示每次变换都在前一次的基础上，矩阵依次在左侧相乘表示每次变换都在最开始的基础上，不管怎么理解，结果总是一样的。
　　计算雅克比矩阵需要对这个矩阵求导，我们在数学软件中求导试试。关于x轴转动变量的求导命令如下。我也不知道为什么要加负号。

D[(RotationMatrix[-y, {0, 1, 0}].RotationMatrix[-x, {1, 0, 0}].RotationMatrix[-z, {0, 0, 1}]), x] /. {Cos[x_] :> Subscript[c, x], Sin[x_] :> Subscript[s, x]} // MatrixForm

　　求导的结果如下：

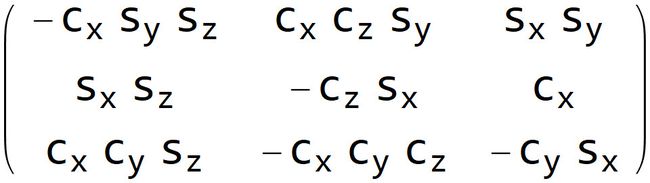
　　与代码中的arx中的计算公式完全相同，我已经检验过了。剩余的ary、arz计算过程同理，我就不列举了。

5.3　laserMapping代码

　　main函数是主体，其中也使用了ros::Rate rate(100)，也就是说这个程序也是按照固定的频率运行的。

参考文献

[1]　An ICP variant using a point-to-line metric.