基于卷积神经网络的图像超分辨率[译文]

文章及代码地址： http://mmlab.ie.cuhk.edu.hk/projects/SRCNN.html

摘要：我们针对单一图像超分辨率（SR）提出了一种深度学习的方法。我们的方法直接学习低/高分辨率图像之间的端对端映射。映射表现为一个深度卷积神经网络（CNN）[15]，它将低分辨率图像作为输入，将高分辨率图像作为输出。我们进一步证明了传统的基于稀疏编码的SR方法可以被看做为CNN。但是不像传统的方法分开处理每个部件，我们的方法共同优化了所有的层。我们的深度CNN有轻量的结构，但是也展现出先进的重建质量，并且在实际在线使用中展现了较块的速度。

关键词：超分辨率重建，深度卷积神经网络

1 介绍

  单一图像超分辨率（SR）是在计算机视觉中的经典问题。最近最先进的SR方法主要是基于样本的。这些方法不仅利用了内部相似的图像，也从外部的低/高分辨率图像的样本对中学习到了映射函数[2, 4, 9, 13, 20, 24-26, 28]。外部的基于样本的方法通常提供了丰富的示例，但是被复杂和紧凑的数据建模所挑战。

  基于稀疏编码的的方法[25, 26]是基于外部样本的SR的一种重建方法。这种方法表现为以下步骤：首先，从图像的过程中密集地提取重叠的块并进行预处理（比如减去平均值）。之后，这些块被低分辨率字典编码。稀疏系数传入高分辨率字典，用于重建高分辨率块。重叠的重建块被聚合（或通过加权平均）来产生最终的输出。这样的SR方法特别关注于去学习和优化字典[25,26]或者寻找可替代的建模方法[4, 2]。然而在这个过程中，剩下的步骤很少能在统一的优化结构中被优化，或者被考虑。

  本文中，我们将深度CNN[15]等价的表示出上文提到的过程（更多细节在3.2节），受到这个事实的启发，我们直接考虑了一个CNN，学习从低/高分辨率图像的端对端映射。我们的方法从根本上是不同于现有的基于外部样本的方法的，我们的方法并不直接学习到用于空间块建模的字典[20,25,26]或者流形[2,4]。这些都是隐式地通过隐藏层来实现的。此外，小块的提取和聚合都作为卷积层形成，因此也都参与了优化。在我们的方法中，整个SR过程都通过学习来获得，几乎没有预处理和后处理。

图1.所提出的基于卷积神经网络的图像超分辨率（SRCNN）仅使用少量的训练迭代就超过了通过双立方插值基线，并优于有适度训练的基于稀疏编码的方法（SR）[26]。更多的训练迭代能进一步提升性能。更多的细节在4.1节中提供（基于提升因子3以及Set5数据集）。该方法提供了从低分辨率图像上、视觉上吸引人的重建。

  我们把提出的模型称作基于卷积神经网络的图像超分辨率方法（SRCNN）。SRCNN有一些很好的性质。首先，它的结构是故意设计得简单，但相比于最先进基于样本的方法，也提供了相同的优秀的精准性。图1展示了与例子的对比。第二，我们的方法因为中等数量的过滤器和层数，所以在实际在线使用中甚至是CPU上，也实现了很快的速度。我们的方法比基于样本的方法要快，因为它是完全前馈的，并且不需要在使用上解决任何优化问题。第三，实验表明，当(i)可以得到更多的数据，和/或(ii)使用更大的模型的时候，网络的修复质量可以得到进一步改善。相反，更大的数据集和模型对于目前的基于样本的方法是一种挑战。

总之，本研究的贡献主要分为三个方面：
1、我们提出了一种基于卷积神经网络的图像超分辨率方法。网络直接学习一个端对端的低/高分辨率图像之间的映射，除了优化之外，几乎没有预处理或后处理。
2、我们建立了我们的基于深度学习的SR方法和传统的基于稀疏编码的SR方法之间的联系，该联系指导了对网络结构的设计。
3、我们证明了深度学习在SR的经典计算机视觉问题上的作用，并且可以实现良好的质量和速度。

2 相关工作

图像超分辨率。一种目前最高水准的SR方法是学习从低/高分辨率块之间的映射[9,4,25,26,24,2,28,20]。这些研究在如何在紧凑的字典或者流形空间中学习相关的低/高分辨率块上是不同的，并且在如何在空间进行重建的策略上也是不同的。在Freeman等人[8]之前的工作中，字典直接可以表现为低分辨率图像和高分辨率图像的小块对，并且可以在低分辨率空间中发现输入小块中的最近邻（NN），这样的小块随着高分辨率小块一起作用于重建工作。Chang等人[4]引入了流形嵌入技术替代NN策略。Yang等人[25,26]的工作中，上述的NN通信发展到更复杂的稀疏编码公式上。这种基于稀疏编码的方法和它的一些改进方法[24,20]是目前最高水准的SR。在这些方法中，小块是被优化的重点；小块的抽取和聚合步骤可以分别看做为预处理和后处理。

卷积神经网络。卷积神经网络（CNN）可以回溯于几十年前[15]，并且最近展现出了爆炸性的流行，部分是由于它在图像分类中的出色表现[14]。几个因素至关重要：(i)在现代强大的GPUs的实现有效训练，(ii)修正线性单元（ReLU）的提出，它可以在保持良好质量的基础上使得收敛过程更快，(iii)可以容易获得大量数据（就像ImageNet[5]）并用于训练更大的模型。我们的方法从这些因素中受益。

基于深度学习的图像重建。已经有一些基于深度学习技术进行图像恢复的研究。多层感知器（MLP），所有的层都是全连接的（与卷积层相反），用于自然图像去噪[3]和去模糊降去噪[19]。与我们的工作更为相关的是，CNN应用于自然图像去噪[12]和去除噪声特征（污渍/雨）[6]。这些恢复问题或多或者少是去噪驱动的。相反，据我们所知，图像超分辨率重建问题并没有从深度学习技术中得到应用。

3 基于卷积神经网络的图像超分辨率

3.1 公式

  考虑单图像超分辨率。我们首先使用双立方插值来提升它到所需要的尺寸，这个过程是我们执行的唯一预处理。插值后的图像记做Y，我们的目标是将Y恢复为图像F(Y)，F(Y)与真实的高分辨率图像X尽可能相似。方便演示，尽管Y有着与X相同的大小，我们仍称Y为“低分辨率”图像。我们希望学习到映射F，F从概念上由三个操作组成：

1、小块的提取和表示：这个操作从低分辨率图像Y提取（重叠）小块，并将每个小块表示为高维向量。这些向量包含一组特征映射，其数量等于向量的维度。
2、非线性映射：这个操作将每个高维向量非线性映射到另一个高维向量上。每个映射向量在概念上是高分辨率的表示块。这些向量包含了另一组特征映射。
3、重建：这个操作聚合了上述表示高分辨率的小块，并用于产生最终的高分辨率图像。这个图像将类似于真实图像X

  我们将会显示所有这些操作形成的CNN，网络的概述如图2所示。接下来我们会对每个操作进行详细说明

图2. 给定低分辨率图像Y，SRCNN的第一层卷积层提取了一组特征图。第二层将这些特征图非线性地映射到高分辨率小块进行表示。最后一层与一个空间邻域内的预测值组合，来产生最后的图像F(Y)

小块的提取和表示。图像超分辨率流行的策略(例如[1])是去密集地提取小快，并且通过一组的预训练的基底来表示他们，比如PAC，DCT，Haar等。这等价于通过一组滤波器对图像进行卷积，每个滤波器都是一个基础。在我们的公式中，我们涉及了对这些基础的优化和对整个网络的优化。正式地，我们的第一层表示为操作F1：

  W1和B1分别代表滤波器和偏置。这里，W1的大小为c×f1×f1×n1。c1是在输入图像中通道的数量，f1是滤波器的空间大小，n1是滤波器的数量。直观来说，W1在图像上进行n1次的卷积操作，并且每个卷积核的大小为c×f1×f1。输出由n1个特征图组成。B1是n1维的向量，该向量的每个元素都与一个滤波器相对应。我们应用ReLU函数（max（0，x））[18]在滤波器响应上。

非线性映射。第一层将每个小块都提取了n1维特征，在第二个操作中，我们将每个n1维向量映射成n2维的向量。这等价于将n2个1×1尺寸的滤波器应用在简单空间上。第二层操作为

  这里，W2的大小为n1×1×1×n2，B2为n2维向量。每个输出的n2维向量在概念上是用于重建的、高分辨率的表示小块。

  可以添加更多的卷积层（空间大小为1×1）来增加非线性性。但这会显著增加模型的复杂度，并因此需要更多的训练时间和数据。本文中，我们选择使用单个卷积层，因为它已经提供了很好的质量。

重建。在传统方法中，预测重叠的高分辨率小块通常会平均起来以形成最终的完整图像。平均可以看作为在一组特征图上预定义的滤波器（特征图的每个位置都是高分辨率小块的“平展”的矢量形式）。基于此，我们定义一个卷积层以产生最后的高分辨率图像：

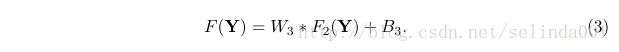
这里，W3的大小为n2×f3×f3×c，B3是一个c维向量

  如果高分辨率小块的表示是在图像域中（我们可以简单地重塑每个表示形成的小块），我们期望滤波器的行为就像平均滤波器；如果高分辨率小块的表示是在其他域（比如就基底而言的系数），我们预计W3将投射系数到图像域上，然后进行平均。无论哪种方式，W3都是一组线性滤波器。
  有趣的是，尽管前面3种操作是出于不同的直觉，但它们都导致了与卷积层的相同形式。我们将三种操作放在一起，形成了卷积神经网络（图2）。在这个模型中，所有的滤波器的权值和偏置都被优化了。
  尽管整个网络结构比较简洁，我们的SRCNN模型也是通过超分辨率的重大进展中得出的广泛经验而精心开发的[25,26]。我们将在下一部分对关系进行详细说明。

图3. 以卷积神经网络的视角描述基于稀疏编码方法

3.2 与基于稀疏编码方法的关系

  我们展示了基于稀疏编码的方法[25,26]，它可以被看做为CNN。图3做出了图示

  在基于稀疏编码的方法中，让我们考虑从输入图像中提取一个f1×f1的低分辨率小块。这个小块被他们的平均值给减去了，之后被投射于（低分辨率）字典上。如果字典的大小是n1，这就等价于在输入图像上（平均减法也是线性运算）使用n1个线性滤波器（f1×f1）。（如图3左侧）

  稀疏编码的解算器将应用于投射的n1系数（参见看特征符号解码器[17]）。解码器的输出是n2个系数，并且在稀疏编码的过程中通常n2=n1。这些n2系数表示高分辨率小块。在这样的情况下，稀疏编码器表现为非线性映射算子。参见图3的中间部分。然而，稀疏编码解码器不是前向反馈的，它是迭代算法。相反，我们的非线性算子是完全前馈的，并且可以非常高效的计算的。我们的非线性算子可以看做为像素级的全连接层。

  上述的n2个系数（在稀疏编码后）之后投射到其他（高分辨率）字典上以产生高分辨率小块。然后重叠高分辨率小块并取平均值。基于上述讨论，这等价于在n2特征图上进行线性卷积。如果重建高分辨率小块的大小为f3×f3，那么线性滤波器也有等价的空间大小f3×f3。（如图3的右侧）

  上述的讨论表明，基于稀疏编码的SR方法可以被看做一种CNN（具有不同的非线性映射）。但非所有的操作都被认为是基于稀疏编码的SR的优化方法。相反，我们的CNN网络中，低分辨率字典、高分辨率字典，非线性映射，平均减法和平均一起，都参与到要优化的滤波器中进行优化。因此我们的方法优化了所有操作组成的端对端映射。

  上述的类比可以帮助我们去设计超参数。例如，我们可以设置最后一层的滤波器的大小比第一层的小，这样我们更加依赖高分辨率小块的中心部分（极端的来说，如果f3=1，我们则使用没有平均的中心像素）。我们也可以设定n2

3.3 损失函数

  学习端对端的映射函数F需要估计参数Θ={W1,W2,W3,B1,B2,B3}，它的实现需要最小化在重建图像F（Y；Θ）与高分辨率图像X之间的损失。考虑一个高分辨率图像集{Xi}以及对应的低分辨率图像{Yi}，我们使用均方误差（MSE）作为损失函数。

  n是训练样本的数量。使用具有标准反向传播的随机梯度下降法使损失最小化。[16]
  使用MSE作为损失函数更有利于高PSNR。PSNR是定量估计图像重建质量的一种广泛使用的度量，并且至少部分地与感知质量有关。值得注意到的是，如果只有损失函数可推导，CNN并不排除使用其他类型的损失函数。如果在训练过程中给出更好的感知度量，它能够灵活的针对网络去适应度量。我们将会在未来研究这个问题。相反，这样的灵活性通常来说对于传统的“手工”方法是很难实现的。

4 实验

待更新…..