人智导（七）：回归分析

人智导（七）：回归分析

问题引入

• 给出一组示例，估算/还原出函数f：
  
• 基于示例的学习（归纳学习）：未知$f$，已知的是一个示例集合（训练集），求得一个或多个函数$f^{\prime }$（模型、假设），使得$f^{\prime }$近似于$f$
  举例：
  
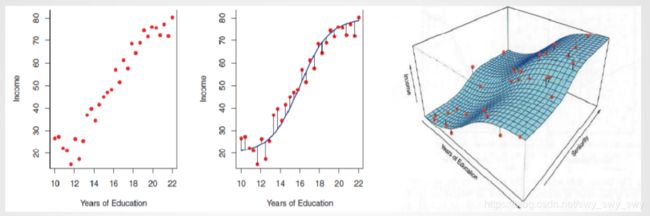
  30个无产者的数据：收入与受教育年限

问题模型

问题描述

给出一组观测变量$X=(x_1,x_2,\dots ,x_p)$以及响应变量$Y$（连续值）
$X$与$Y$之间存在关联，即
$$Y=f(X)+ϵ$$
其中$f$是未知的函数，$ϵ$是随机错误（均值为零）
任务：已知一组观测数据（$X$，$Y$）取值，估算出$f$
目的：预测和推理（解释）

预测的目的

• 在许多现实应用中，输入变量$X$是可预测的，但输出变量$Y$的实际值不易直接观测到
• 试图预测真实的$Y$，通过$Y^{\prime }=f^{\prime }(X)$
• $f^{\prime }$表示未知$f$的预估，$Y^{\prime }$表示预测的结果
• 回归技术：估算$f$，使得误差（残差）平方均值最小化$$E(Y-Y^{\prime }{)}^{2}or[f(X)-f^{\prime }(X){]}^2$$

目标函数：均方误差最小

$$RSS=e_1^2+e_2^2+\cdots +e_n^2=(y_1-y_1^{\prime }{)}^2+(y_2-y_2^{\prime }{)}^2+\cdots +(y_n-y_n^{\prime }{)}^2$$
均方误差$MSE=\frac{RSS}{n}$最小化
数学期望（均值）：$\mu =\frac{{\Sigma }_{i=1}^n{y}_i}{n}$
方差：度量随机变量与其数学期望（即均值）之间的偏离程度${\sigma }^2=\frac{{\Sigma }_{i=1}^n(y_i-\mu {)}^2}{n}$
标准差：$\sigma$

推理的目的

估算$f$，是理解$X$与$Y$之间的关系
具体地，回答以下问题：

• $(x_1,x_2,\dots ,x_p)$中哪些变量与$Y$关联？
• $Y$与$(x_1,x_2,\dots ,x_p)$中的每一变量的关系是什么？是正/负相关性？
• $Y$与$(x_1,x_2,\dots ,x_p)$中每一变量的关系能否线性地概括？或需要更复杂的方程表示？

应用示例：为客户改善其产品销售提供咨询

• 数据集：某商业客户产品在数百家商场的销售量以及三种不同媒体（电视、电台广播、报纸）在每家广告费用支出的历史数据。
• 应用目的：
  • 开发一个精确的预测模型，能基于这三种媒体费用的预算预测该产品销售量$$sales=f(tv,radio,newspaper)$$
  • 解答问题，如：
    • 哪种媒体对销售有贡献？
    • 哪种媒体对销售量的提升贡献最大？
    • TV广告费用的增长将导致多少销售量的增长？

基于示例的学习

如何估算$f$？
已有一组观察数据（训练数据）：
$\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，$x_i$是$p$个元素的矢量
通过已观察到的（训练）数据估算未知的$f$，发现$f^{\prime }$，使得$Y\approx f^{\prime }(X)$
两类通用的方法：参数化方法与非参数化方法

参数化方法：基于模型的方法

第一步：假设函数$f$的形式/形状，如$f$假设是线性的（模型）
$$f(X)={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_p{X}_p$$
第二步：使用训练数据，来训练这个模型。问题简化成估算参数的值${\beta }_0,{\beta }_1,\dots ,{\beta }_p$
$$Y\approx {\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_p{X}_p$$
特点：

• 泛化能力强(generalization)
• 解释性强，适于判断X与Y的关联（推理）
  参数化方法弱处：
  有可能与真实的$f$形状非常不同，预测精度相差较大。

非参数方法

• 不假设$f$的形式/形状，而是尽可能地拟合观察（训练）数据
• 特点：可以拟合更多形式/形状的$f$，故预测精度高
• 缺点：需要大量的观察数据（训练数据），以便训练一个有精度的模型（针对$f$），否则容易过拟合(overfitting)

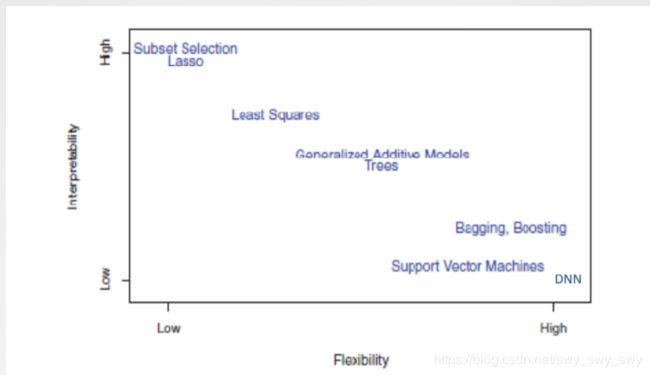
预测精度与模型可解释性的权衡

• 参数化方法：不灵活、更受限（估算的$f$形状局限于小范围内）
• 非参数方法：更灵活的（拟合性好）、估算的$f$形状在大范围内变化
• 既然有更灵活的方法，为何选择应用比较受限的方法？
  • 以推理/解释为目的。线性模型易于解释各观测变量X与响应变量Y之间的关系
  • 而描述形状更灵活的方法如SVM、Bagging&Boosting、DNN等理解观测变量X与响应变量Y间的关联是很困难的
    如下图：
    

回归

线性回归

• 最简单形式的线性回归：单一观测变量 $$Y={\beta }_0+{\beta }_{1}X$$ 已知有一组观察数据（训练数据）：$\{(x_1,y_1),(x_2,y_2),\dots ,(x_n,y_n)\}$，其中第i个观测数据的误差（残差）：$e_i=y_i^{\prime }-y_i$；目标是求得参量${\beta }_0$和${\beta }_1$以最小化误差（损失）函数$$Loss(\beta )={\Sigma }_{i=1}^n(y_i^{\prime }-y_i{)}^2$$
• 最小二乘法：$${\beta }_1=\frac{{\Sigma }_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{{\Sigma }_{i=1}^n(x_i-\bar{x}{)}^2}$$ $${\beta }_0=\bar{y}-{\beta }_1\bar{x}$$ $$\bar{x}={\Sigma }_{i=1}^n\frac{x_i}{n}\bar{y}={\Sigma }_{i=1}^n\frac{y_i}{n}$$
  举例：
  
  ${\beta }_1=3.5{\beta }_0=23.6Y\approx 23.6+3.5X$
  预测10年工龄员工的工资：58.6k

多元线性回归

• 多元回归模型：$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+\cdots +{\beta }_n{X}_n$$示例：$$sales={\beta }_0+{\beta }_1\times radio+{\beta }_2\times tv+{\beta }_3\times newspaper$$
• 极小化损失函数（目标函数）：$$Loss(\beta )={\Sigma }_{i=1}^n(f_{\beta }^{\prime }(x_i)-y_i{)}^2$$
• 最小二乘法求解参数 $$\begin{gathered} Loss(\beta )={\Sigma }_{i=1}^n{e}^2={\Sigma }_{i=1}^n(y^{\prime }-y{)}^2 \\ =e^{\prime }e=(Y-Y^{\prime }{)}^{\prime }(Y-Y^{\prime })=(Y-X\beta {)}^{\prime }(Y-X\beta ) \\ =Y^{\prime }Y-{\beta }^{\prime }{X}^{\prime }Y-YX\beta +{\beta }^{\prime }{X}^{\prime }X\beta \\ =Y^{\prime }Y-2{\beta }^{\prime }{X}^{\prime }Y+{\beta }^{\prime }{X}^{\prime }X\beta \end{gathered}$$上式求偏导极小化损失函数： $$\frac{\partial Loss(\beta )}{\partial \beta }=\frac{\partial (Y^{\prime }Y-2{\beta }^{\prime }{X}^{\prime }Y+{\beta }^{\prime }{X}^{\prime }X\beta )}{\partial \beta }=-2X^{\prime }Y+2X^{\prime }X\beta =0$$ 因此$\beta =(X^{\prime }X{)}^{-1}{X}^{\prime }Y$

回归模型的线性假设

• 线性回归假设一
  • 观测变量$X=(X_1,X_2,\dots ,X_p)$与响应变量间的关系是累加性(additive)的（变量独立）$$Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2$$
  • 例如有两个观测变量时，扩展考虑变量间的相关性，示例：$$\begin{gathered} Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_1{X}_2 \\ Y={\beta }_0+({\beta }_1+{\beta }_3{X}_2)X_1+{\beta }_2{X}_2 \\ Y={\beta }_0+\widehat{{\beta }_1}{X}_1+{\beta }_2{X}_2 \end{gathered}$$ $$sales={\beta }_0+({\beta }_1+{\beta }_3\times radio)\times yv+{\beta }_2\times radio$$
• 线性回归模型假设二
  • 观测变量X与响应变量Y间的关系是线性的
  • 多项式回归，扩展地表示非线性关系为多元线性回归$$Y={\beta }_0+{\beta }_{1}X+{\beta }_2{X}^2+{\beta }_3{X}^3+\cdots +{\beta }_n{X}^n$$
  • 例如$n$取值为3：$$\begin{gathered} Y={\beta }_0+{\beta }_1{X}_1+{\beta }_2{X}_2+{\beta }_3{X}_3 \\ {X}_1=X{X}_2=X^2{X}_3=X^3 \end{gathered}$$

Logistic回归

引入

有两种预测问题：

• 响应变量Y是连续型（数值型）：线性回归，用于数值型问题解决
• 响应变量Y是离散型（类目型）：逻辑(Logistic)回归，用于分类问题解决
• 二元分类问题（0，1）
  • 并不直接模型化响应变量Y
  • Logistic回归模型化Y属于一个特定类的概率，即模型化$Pr(Y=0|X)$与$X$的关系

Logistic回归

• Logistic函数（Sigmoid函数） $$f(z)=\frac{1}{1+e^{-z}}$$ $$z={\beta }_0+{\beta }_1{X}_1+\cdots +{\beta }_n{X}_n$$
• [0,1]区间平滑曲线，且$f(z)+f(-z)=1$
• 二元分类：$$P(y=0|z)=f(z)$$ $$P(y=1|z)=1-f(z)$$

Logistic回归与贝叶斯方法

二分类（类C1：y=0；类C2：y=1）
$$\begin{gathered} P(C1|X)=\frac{P(X,C1)}{P(X)}=\frac{P(X|C1)P(C1)}{P(X)} \\ =\frac{P(X|C1)P(C1)}{P(X|C1)P(C1)+P(X|C2)P(C2)} \\ =\frac{1}{1+e^{-\alpha }} \end{gathered}$$
其中
$$\alpha =ln\frac{P(X|C1)P(C1)}{P(X|C2)P(C2)}$$
逻辑回归（判别模型）
极大似然估计：决定最优参数${\beta }^{\ast }$: $${\beta }^{\ast }\leftarrow ar{g}_{\beta }max{\Pi }_{i=1}^{m}P(Y_i|X_i,\beta )$$
目标函数：求全局最优解
$$\begin{gathered} f(\beta )={\Sigma }_{i=1}^m[Y_{i}lnP(Y_i=1|X_i,\beta )+(1-Y_i)lnP(Y_i=0|X_i,\beta )] \\ ={\Sigma }_{i=1}^m[Y_{i}ln\frac{P(Y_i=1|X_i,\beta )}{P(Y_i=0|X_i,\beta )}+lnP(Y_i=0|X_i,\beta )] \\ ={\Sigma }_{i=1}^m[Y_i({\beta }_0+{\Sigma }_{j=1}^n{\beta }_j{X}_i^{(j)})-(1+exp({\beta }_0+{\Sigma }_{j=1}^n{\beta }_j{X}_i^{(j)}))] \end{gathered}$$
朴素贝叶斯（生成模型）
二元分类$Y\in \{0,1\}$: $$P(Y|X)=\frac{P(X,Y)}{P(X)}=\frac{P(X|Y)P(Y)}{P(X)}$$
条件独立性假设$X=(x_1,x_2,\dots ,x_n)$: $$P(X|Y)={\Pi }_{i=1}^{n}P(x_i|Y)$$
假设在Y类中变量$x\in X$的概率分布服从高斯（正态）分布
概率密度函数 $$P(x|Y)=\frac{1}{\sqrt{2\pi }{\sigma }_k}{e}^{-\frac{(x-{\mu }_k{)}^2}{2{\sigma }_k^2}}$$