DLX算法及应用(三)杀手数独
(马上就要开学了,抽空把这个坑填上。。。。。。)
先来介绍下什么是杀手数独
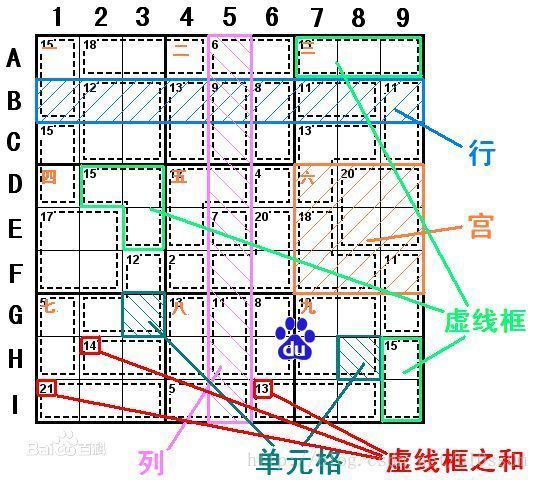
如图所示(来源:百度百科),杀手数独就是在经典数独的基础上,又多加了一组限制条件:每一个虚线框称作一个区,要求区内的数字不能重复,且区内数字总和等于该区左上角的数字。
杀手数独起始是没有一个数字的,挺难的= =
好像在哪里看到这样一个提问:杀手数独为什么叫杀手数独?---因为是时间的杀手。。。。。= =
想体验的可以去欧泊颗(http://www.oubk.com/)感受一下。
正好之前在研究DLX算法,就想试试能不能将杀手数独转换为一个精确覆盖问题,网上搜了好久也没有发现相关的资源,估计没人这么无聊吧= =,那我就自己试着构造一下吧。
以下正文:
首先来回顾一下经典数独是怎么转换成一个324列的精确覆盖问题的,见《DLX算法及应用(一)DLX模板+解数独》(http://blog.csdn.net/bl0ss0m/article/details/17918705)
那么杀手数独就是在经典数独的4个限制条件基础上,新增了一条:
虚线框内数字不重复且和为给出的数字
那么我们就再新增405列(因为81个格子总和为405),其中将405列分成若干组,每一组就代表了一个虚线框,每一组的列数就为对应虚线框中数字之和
让我们单独拿出一个虚线框来考虑:
对于一个包含了{a1,a2,...,an}n个格子和为Sn的虚线框,我们令
Sn = a1+a2+...+an (1 ≤ a1 < a2 < ... < an ≤ 9)
这样a1最小为max{1, Sn-(n-1)(20-n)/2},最大为[Sn/n - (n-1)/2]下取整
假设其包含了3个格子,和为20,那么它就对应了20列
可能的情况就为
3+8+9
4+7+9
5+6+9
5+7+8这样,任意一个格子都可能是{3,4,5,6,7,8,9}中的一个
但如果第一个格子为3,剩下2个格子就只可能为8、9
如果第一个格子为4,剩下2个格子就只可能为7、9
.....
如何用01矩阵表达这种关系呢?
再观察下上面的4种情况,发现3、4、5只可能出现在最开始的位置,6只可能跟在5的后面,7可以跟在4或5的后面,8可以跟在3的后面,也可在最后,9只可能在最后
也就是说有1种3、4、5、6、9,2种7、8,也就是说一个格子可能为上述9种可能中的一种,那我们这样构造:
第一个格子可能为3,前324列和经典数独的构造方式一样,在该虚线框对应的列组中,前3列为1
可能为4,前4列为1
可能为5,前5列为1
可能为6,第6~11列为1
可能为7(1),第5~11列为1
可能为7(2),第6~12列为1
可能为8(1),第4~11列为1
可能为8(2),第13~20列为1
可能为9,第12~20列为1
剩下的2个格子同样如此
再举个直观的例子:5 = 1+4、2+3,构造的矩阵如下
... 0 ... 1 ... 1 0 0 0 0 ...
... 0 ... 1 ... 1 1 0 0 0 ...
... 0 ... 1 ... 0 0 1 1 1 ...
... 0 ... 1 ... 0 1 1 1 1 ...
... 1 ... 0 ... 1 0 0 0 0 ...
... 1 ... 0 ... 1 1 0 0 0 ...
... 1 ... 0 ... 0 0 1 1 1 ...
... 1 ... 0 ... 0 1 1 1 1 ...如果先选择了第1行,那么根据位置信息,就会排除掉2~4行,再根据虚线框的信息,排除掉5、6行,第7行无法完全覆盖,所以选择第8行,即1+4
这样就可以构造出一个若干行,324+405列的01矩阵,再套用我们之前写好的DLX模板,就可以快速的解决杀手数独问题了!!
代码什么的麻烦各位去下一下,所需积分0,给我加点资源分吧^_^
下载地址:
杀手数独例题及程序:
http://download.csdn.net/detail/u012453913/6924545
源代码:
http://download.csdn.net/detail/u012453913/6925003