知识图谱（八）——知识存储和检索

背景

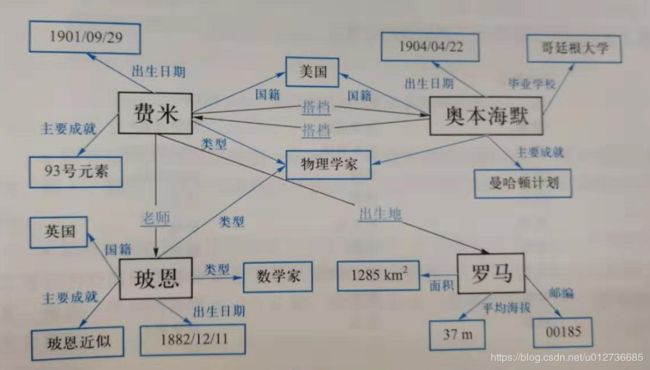
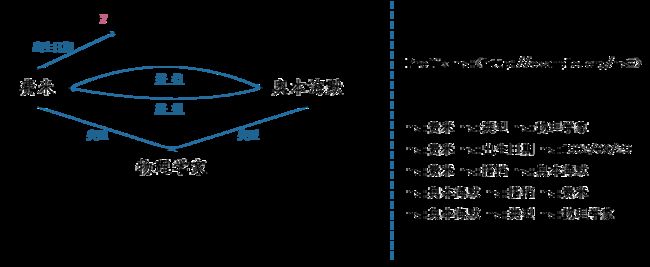
知识图谱是一种有向图结构，描述了现实世界存在的实体、事件或者概念以及它们之间的关系，为自动问答、信息检索等应用提供支撑。其中，图中的节点表示实体、事件或概念，图中的边表示相邻节点间的关系，如下图所示。

• 每一个节点表示一个实体，每个实体都是某一抽象概念的实例。这些抽象概念被称为实体类型，如：人物、城市等。
  • 实体除了具有类型信息，还具有丰富的属性信息（蓝色部分），这些属性信息用于刻画实体的内在特性。
    

一、知识图谱的存储

知识图谱中的知识是通过RDF进行表示的，其基本构成单元是事实。每个事实是一个三元组 (S, P, O)

• S 是主语（Subject），其取值可以是实体、事件或概念中的任何一个；
• P 是谓语（Predicate），其取值可以是关系或属性；
• O 是宾语（Object），其取值可以是实体、事件、概念或普通的值（eg：数字、字符串等）

知识表示的三元组列表 示例如下：

RDF数据

<费米,		主要成就,		93号元素>
<费米,		出生日期,		1901/09/29>
<费米,		类型,			物理学家>
<费米,		国籍,			美国>
<费米,		出生地,			罗马>
<费米,		老师,			玻尔>
<玻恩,		主要成就,		玻恩近似>
<玻恩,		类型,			物理学家>
<玻恩,		类型,			数学家>
...			...				...

按照存储方式的不同，可分为：基于表结构的存储 和 基于图结构的存储

1、基于表结构的存储

利用二维数据表对知识图谱中的数据进行存储，常见的设计方法有：三元组表、类型表、关系数据库等

（1）三元组表

成熟产品：Jena、Oracle、Sesame、3store、SOR、Rstar 和 Virtuoso。

优点：简单直接、易于理解；
缺点：

• 整个知识图谱都存储在一张表中，导致单表的规模太大。对大表进行查询、插入、删除、修改等操作的开销很大，这将导致KG的实用性大打折扣。
• 复杂查询在这种存储结构上的开销巨大。由于数据表只包括三个字段，因此复杂的查询只能拆分称若干简单查询的符合操作，大大降低查询的效率。

（2）类型表

为每种类型构建一张表，同一类型的实例存放在相同的表中。表中的每一列表示该类实体的一个属性，每一行存储该类实体的一个实例。

示例：

1. 城市表

主体对象	面积	平均海拔	邮编
罗马	1285 $k{m}^2$	37m	00185

2. 人物表

主体对象	主要成就	国籍	出生日期	出生地
费米	93号元素	美国	1901/09/29	罗马
奥本海默	曼哈顿计划	美国	1904/04/22
玻恩	玻恩近似	英国	1882/12/11

3. 物理学家表

主体对象	主要成就	国籍	出生日期
费米	93号元素	美国	1901/09/29
奥本海默	曼哈顿计划	美国	1904/04/22
玻恩	玻恩近似	英国	1882/12/11

4. 数学家表

主体对象	主要成就	国籍	出生日期
费米	93号元素	美国	1901/09/29

缺点：（然后克服三元组表的不足）

• 大量数据字段的冗余存储。假设知识图谱中既有“数学家”又有“物理学家”，则同属于这两个类别的实例将会同时被存储在这两个表中，其中它们共有的属性会被重复存储。如上面的表 3 与表 4
• 大量的数据列为空值。通常知识图谱中并非每个实体在所有属性或关系上都有值。

解决方法：将知识图谱的类别体系考虑进来。

• 具体来说，每个类型的数据表都只记录属于该类型的特有属性，不同类别的公共属性保存在上一级类型对应的数据表中，下级表继承上级表的所有属性。下图为考虑层级关系的类型表，（a）为人物相关的类别体系，（b）为该类别体系下设计的类型表。
  
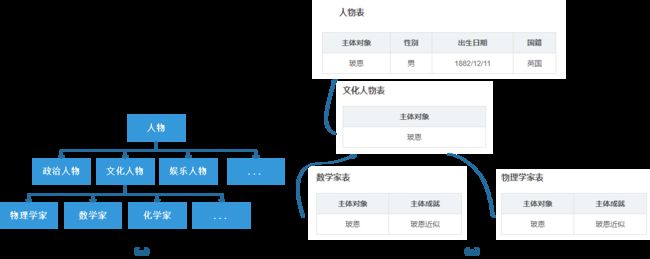
  缺点
• 由于类型表的不同字段表示不同的属性或关系，因此查询时必须指明属性或关系，无法做不确定属性或关系的查询。
• 由于数据表是和具体类型对应的，不同类型的数据表具有不同的结构，因此在查询之前必须知道目标对象的类型才能确定查找的数据表。则需要维护一个“属性-类型”映射表，以便在进行属性查询时可以根据目标属性确定类型。
• 当查询涉及不同类型的实体时，需要进行多表的链接，该操作开销巨大，限制KG对复杂查询的处理能力。
• KG包含丰富的实体类型，因此需要创建大量的数据表，并且这些数据表之间又具有复杂的关系，增加管理难度。

（3）关系数据库

关系数据库通过 属性 对现实世界中的事物进行描述。

• 每个属性的取值范围所构成的集合，称为对应属性的 域
• 属性的取值只能是原子数据。
  • 原子数据：不能进步拆分的数据，eg：整数、字符串等
  • 非原子数据：由多个原子数据构成，可进步拆分，eg：集合、列表、元组等。
• 关系数据库以二维表对数据进行组织和存储，表的每一列表示一个属性，每一行表示一条记录。

属性按照各自特点可分为：

• 候选键：能够唯一标识一条记录的最少的属性集合。
  • 唯一性：候选键在整个表的范围内必须具有唯一的值，不同记录不能具有相同的候选键值；
  • 最小性：候选键所包含的属性必须是必不可少的，缺少其中的任何一个都不再具备唯一性。
  • eg：学生的学号、身份证号分为都可以作为候选键，但是（学号，身份证号）这属性组不满足最小性，不能作为候选键。
• 主键：一个数据库包含多个候候选键，从中任意选取一个为主键。一般选择单属性组成的候选键作为主键。
• 外键：数据表中的某个属性或属性组是其他表的候选键，则称为当前表的外键。外键可以保证不同数据表之间数据的一致性。
• 主属性与非主属性：包含在任何候选键中的属性为主属性，不包含在任何候选键中的属性为非主属性。

常见可用于KG的关系数据库：DB2、Oracle、Microsoft SQL Sever、PostgreSQL、MySQL等

2、基于图结构的存储

基于图结构的存储，可直接准确地反映KG的内部结构，有利用对知识的查询，可借鉴图论算法，有利于对知识深度挖掘及推理。

（1）基于图结构的存储模型

• 节点：表示实体，可以定义属性（用于描述实体特性）。
• 边：表示实体之间的关系，可以定义边的属性。

基于图结构的存储，从实体出发，不同实体对应的节点可定义不同的属

（2）常用图数据库介绍

图数据库的理论基础是图论，通过节点、边 和 属性对数据进行表示和存储，具体来说，图数据库基于有向图，其中节点、边、属性是图数据库的核心概念。

• 节点：表示实体、事件等对象。eg：人物、地点、电影等都可作为图中的节点。
• 边：指图中连接节点的有向线条，表示节点之间的关系。eg：人物节点之间的夫妻关系、同事关系等。
• 属性：描述节点或边的特性。eg：人物（节点）的姓名、夫妻关系（边）的起止时间等。

常见图数据库：Neo4j、OrientDB、InfoGrid、HyperGraphDB、InfiniteGraph（分布式）等

• Neo4j：开源、高性能、本地数据库（访问速度快）、轻量级；
• OrientDB：开源文档-图数据库、多模式、本地数据库；
• …

二、知识图谱的检索

1、常见形式化查询语言

KG是通过数据库进行存储的，大部分数据库系统通过形式化的查询语言为用户提供访问数据的接口，关系型数据库的标准查询语言是SQL，图数据库的标准查询语言是SPARQL。

（1）SQL（Structured Query Language，结构化查询语言）

主要功能：对数据的插入、修改、删除、查询四种操作。

示例：Triples表

S	P	O
费米	类型	物理学家
费米	出生日期	1902/09/29
费米	搭档	奥本海默
奥本海默	搭档	费米
奥本海默	出生日期	1904/04/22
奥本海默	毕业院校	阿根廷大学
费米	出生地	罗马
罗马	海拔	37m

• 数据插入——INSERT
  • INSERT INTO 表名 VALUES (值1，值2，...) [,值1，值2，...], ...：值1,值2…分别对应数据表中第一列、第二列，VALUES对应的值的顺序和数量有严格的要求。
  • INSERT INTO 表名 (列1，列2，...) VALUES (值1，值2，...) [,值1，值2，...], ...：指明插入数据的列
  • eg：新增“玻恩”实体及其属性，以及与“费米”的关系（S:费米，P:老师，O:玻恩）
    • INSERT INTO Triples VALUES ('费米','老师','玻恩'),('玻恩','类型','数学家'),('玻恩','类型','物理学家')
    • INSERT INTO Triples (S,P,O) VALUES ('费米','老师','玻恩'),('玻恩','类型','数学家'),('玻恩','类型','物理学家')
• 数据修改——UPDATE
  • UPDATE 表名 SET 列1=值1,列2=值2,... WHERE 条件 其中’条件’指明需修改的数据记录，若不指定，则整个表的数据都被修改。
  • eg：“费米”的出生日期修改为"1901/09/29"
    • UPDATE Triples SET O='1901/09/29' WHERE S='费米' and P='出生日期'
• 数据删除——DELETE
  • DELETE FROM 表名 WHERE 条件 其中’条件’指明需修改的数据记录，若不指定，则整个表的数据都被修改。
  • eg：删除“奥本海默”实体和与其相关的所有边
    • DELETE FROM Triples WHERE S='奥本海默' or O='奥本海默'
• 数据查询——SELECT
  • SELECT 列1, 列2, ... FROM 表名 WHERE 条件、 SELECT * FROM 表名 WHERE 条件
  • eg：查询所有数学家实体
    • SELECT S FROM Triples WHERE P='类型' and O='数学家'
• 此外，SQL还内置函数（最大值、最小值、平均值等）、表连接（JOIN）等

（2）SPARQL语言

SPARQL是由W3C为RDF数据开发的一种查询语言和数据获取协议，被广泛应用于图数据库。

a、数据插入——INSERT DATA

• 基本语法：INSERT DATA 三元组数据，其中三元组数据可以是多条三元组，不同的三元组通过 ‘.’ 分割，用 ‘;’ 可以分割连续插入语前一个三元组的头实体相同的三元组。若待插入的三元组在RDF中已存在，则忽略该三元组。
• eg：向上图表示的RDF中插入以下三元组：

ns:费米  ns:老师  ns:玻恩.
ns:玻恩  ns:类型  ns:数学家.
ns:玻恩  ns:类型  ns:物理学家.

==》对应的 SPARQL 语句

prefix ns: 
INSERT DATA {
ns:费米  ns:老师  ns:玻恩 .
ns:玻恩  ns:类型  ns:数学家 ;
         ns:类型  ns:物理学家 .
}

结果如下所示：

b、数据删除——DELETE DATA

• 基本语法：DELETE DATA 三元组数据，其中三元组数据可以是多个三元组。对于给定的每个三元组，若其在RDF图中，则删除，否则忽略该三元组。
• eg：向上图表示的RDF中删除三元组 (ns:奥本海默 ns:类型 ns:物理学家)，注意删除单个三元组

prefix ns: 
DELETE DATA {
ns:奥本海默 ns:类型 ns:物理学家 .
}

结果如下所示：删除单个三元组

• 删除节点，eg：删除“奥本海默”节点

prefix ns: 
DELETE WHERE {
ns:奥本海默 ?p ?o .
?s ?p ns:奥本海默 .
}

结果如下所示：删除节点

c、数据更新

数据更新是指更新RDF图中三元组的值，SPARQL通过组合 INSERT DATA 语句和 DELETE DATA 语句来实现数据更新的功能。

eg：修改三元组(ns:费米 ns:出生日期 "1902/09/29")修改为(ns:费米 ns:出生日期 "1901/09/29")

prefix ns: 
DELETE DATA {ns:费米 ns:出生日期 "1902/09/29" .};
INSERT DATA {ns:费米 ns:出生日期 "1901/09/29" .}

结果如下：

d、数据查询

四种形式：SELECT、ASK、DESCRIBE 和 CONSTRUCT。

• SELECT：从KG中获取满足条件的数据；
• ASK：用于测试KG中是hi否存在满足给定条件的数据，若存在则返回“YES”，否则为“NO”，该查询不返回具体的匹配数据；
• DESCRIBE：用于查询和制定资源相关的RDF数据，这些数据形成了对给定资源的详细描述；
• CONSTRUCT：根据查询图的结果生成RDF。

SELECT：从KG中获取满足条件的数据；

• 基于语法：SELECT 变量1 变量2 ... WHERE 图模式 [修饰符]
  • SELECT子句 SELECT 变量1 变量2 ...：表示要查询的目标。
  • WHERE子句 WHERE 图模式：为SELECT子句中的变量提供约束，查询结果必须完全匹配该子句给出的图模式。
    • 图模式：主要包含两类元素，一类是三元组。eg：?x a Person表示变量?x必须是Person的一个实例。另一类是通过FILTER关键字给出的条件限制，包括数字大小的限制、字符串格式的限制等。
  • 可选项 [修饰符]：用于对查询结果做一些特殊处理，例如：ORDER子句、LIMIT子句（限制结果数量）等。
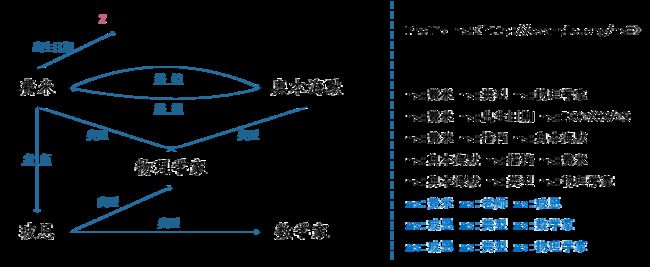
• 示例：查询类型既是“数学家”也是“物理学家”的节点

prefix ns: 
SELECT ?s
WHERE {
	?s   ns:类型   ns:数学家   .
	?s   ns:类型   ns:物理学家   .
}

查询结果

S
玻恩

ASK：用于测试KG中是hi否存在满足给定条件的数据

• 基本语法： ASK 图模式，其中图模式与 SELECT 相同。
• 示例：测试是否存在“费米”老师的节点，对应的语句为：

prefix ns: 
ASK  {	ns:费米   ns:老师   ?o   .}

该语句返回的结果是“yes”，若数据中不存在“费米”的老师节点（即“玻恩”）则返回“no”

DESCRIBE：用于获取与给定资源相关的数据

• 基本语法：DESCRIBE 资源或变量 [WHERE 图模式]
  • DESCRIBE后既可直接跟确定的资源标识符，也可跟变量；
  • WHERE 子句为可选项，用于限定变量满足的图模式。
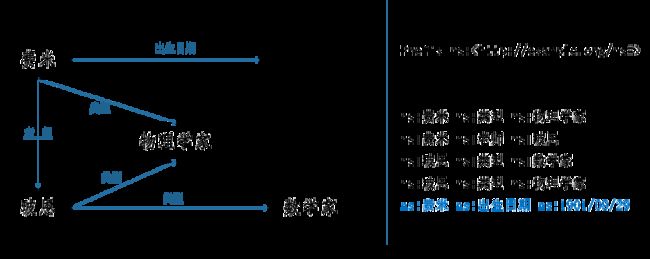
• 示例：获取老师为“玻恩”的节点的所有信息，对应的语句如下：

prefix ns: 
DESCRIBE  ?s  WHERE {?s   ns:老师   ns:玻恩   .}

执行结果如下：

@prefix ns:
ns:费米   ns:类型   ns:物理学家
ns:费米   ns:出生日期   "1901/09/29"
ns:费米   ns:老师   ns:玻恩

CONSTRUCT：用于生成满足图模式的RDF图

• 基本语法：CONSTRUCT 图模板 WHERE 图模式
  • 图模板：确定生成的RDF图所包含的三元组类型，它由一组三元组构成，每个三元组既可以是包含变量的三元组模板，也可以是不包含变量的事实三元组；
  • 图模式，用于约束语句中的变量
• 基本流程：首先执行WHERE子句，从KG中获取所有满足图模式的变量取值；然后针对每一个变量取值，替换RDF图模板中的变量，生成一组三元组。
• 示例：

prefix ns: 
CONSTRUCT {
	?s  ns:搭档  ns:奥本海默  .
	ns:奥本海默  ns:搭档  ?s  .
}
WHERE {
	?s   ns:老师  ns:玻恩  .
}

执行结果为:

@prefix ns:
ns:费米  ns:搭档  ns:奥本海默  .
ns:奥本海默  ns:搭档  ns:费米  .

2、图检索技术

问题的提出：基于图结构的存储方式能够直观灵活地对知识进行表示和存储，而标准的图查询算法复杂度较高，何如提高图查询的效率成为KG研究的重要问题。

定义（即子图匹配问题）：NP完全问题（目前尚不存在多项式时间复杂度内可解决的算法）

• 在给定查询图 $Q$ 和目标图集 $D=\{G_i\}$ 的条件下，在 $D$ 中找出所有与 $Q$ 同构的子图。
• （数学上定义）：图 $G_1(V_1,E_1)$ 和图 $G_2(V_2,E_2)$ 的子图同构，当且仅当存在一个双射函数 $f:V_1\to V_2$，对于 $G_1$ 的任意一条边 $e(v_1,v_2)\in E_1$，都有 $e^{\prime }(f(v_1),f(v_2))\in E_2$。
• 与数学中的区别（优势）：
  • 不会触发子图匹配算法的最坏情况。KG中的图结构通常不会特别复杂，只有少数节点之间有边相连。
  • 利用KG中丰富的标签信息可以有效降低算法的搜索空间。

（1）子图筛选

图索引技术是实现子图筛选的有效方法。在数据预处理阶段进行。

基本原理：首先根据图上的特征信息建立索引，在进行子图匹配时，根据查询图上的特征能够快速地从图数据库中检索得到满足条件的候选子图，避免在全部子图上进行匹配。

常用图索引方法

• 基于路径索引：把图上所有长度小于某特定值的路径收集起来，并根据这些路径为图数据库中的子图建立倒排索引。
  • 匹配过程：首先从匹配图中抽取具有代表性的路径，然后利用索引检索获得所有包含这些路径的候选子图，最后在候选子图上进行同构测试获得最终的结果。
  • 优点：图的路径获取简单直接 ==》构建索引比较方便
  • 缺点：随着路径长度的增加，路径数目呈指数级增长，对于大规模KG，消耗巨大存储空间，增加检索时间；不同路径对子图的区分性差异很大，区分性低的路径对于降低搜索空间的效果有限。
• 基于子图的索引方法：将子图作为索引的特征。
  • 关键问题：如何在保证区分性的条件下减小索引的规模。
  • 常用方法：在构建索引时，通过在KG上挖掘出频繁子图作为建立索引的依据。
    • 频繁子图的衡量指标：频繁度——子图出现的次数
    • 频繁度的设置需精心挑选。

（2）子图同构判定

常用算法：Ullmann算法（也称枚举算法）——能够枚举出所有的同构子图